Содержание
- 2. Можно привести лошадь на водопой, но нельзя заставить ее пить. Поговорка североамериканских индейцев
- 3. Информация, сообщение, сигнал, канал связи Информация - это сведения, знания, новости, идеи и т.п. Информация -
- 4. Канал связи – совокупность технических средств для передачи сообщений определенного вида из одного пункта в другой.
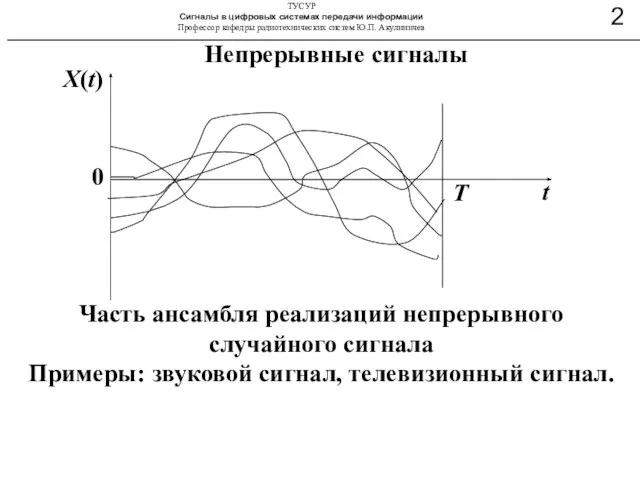
- 5. Непрерывные сигналы Часть ансамбля реализаций непрерывного случайного сигнала Примеры: звуковой сигнал, телевизионный сигнал. X(t) 0 t
- 6. Любой сигнал u(t) можно представить как сумму колебаний разных частот. Спектр непрерывного сигнала u(t)– это комплексная
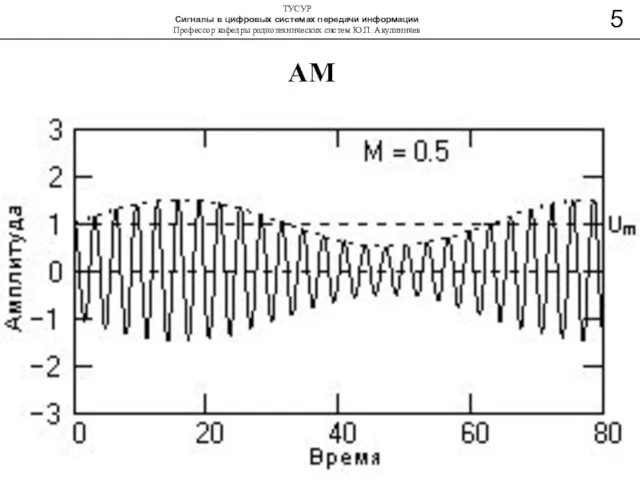
- 7. АМ
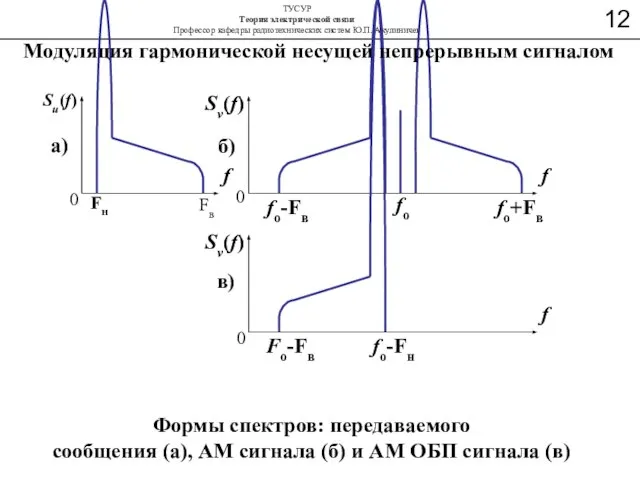
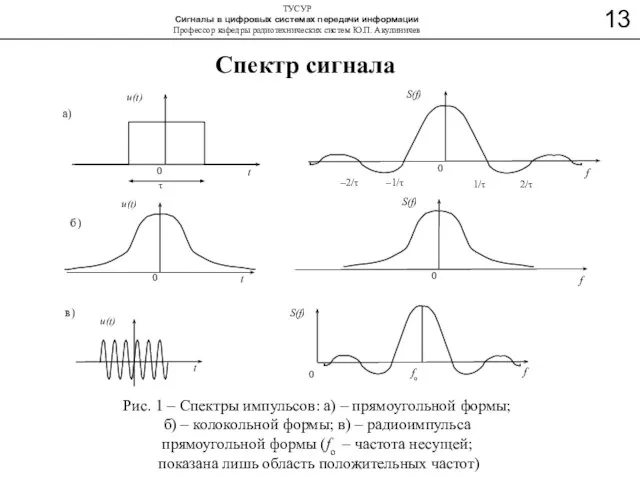
- 8. а) Sv(f) Формы спектров: передаваемого сообщения (а), АМ сигнала (б) и АМ ОБП сигнала (в) б)
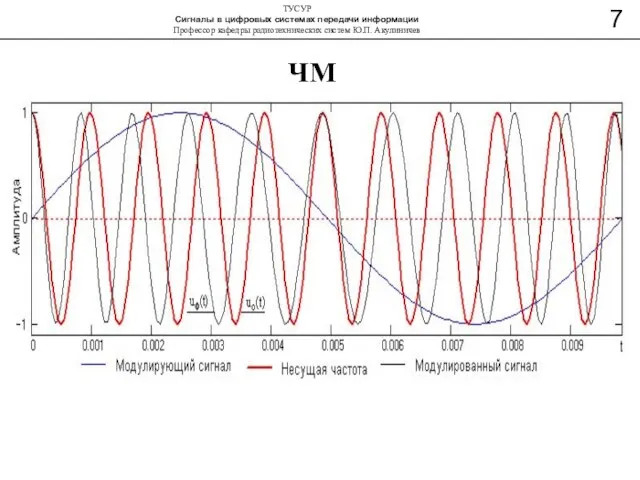
- 9. ЧМ
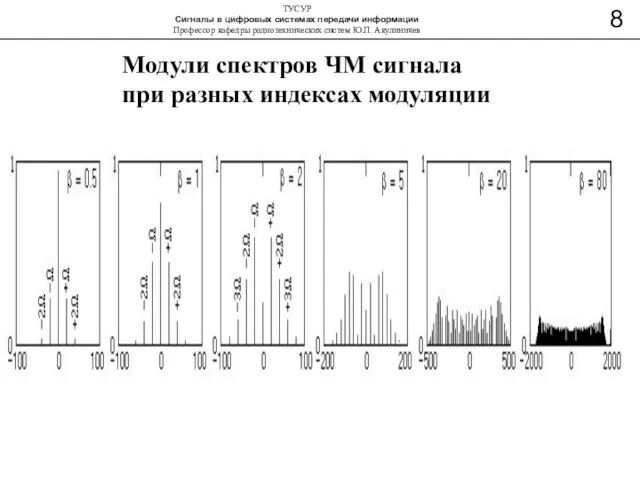
- 10. Модули спектров ЧМ сигнала при разных индексах модуляции
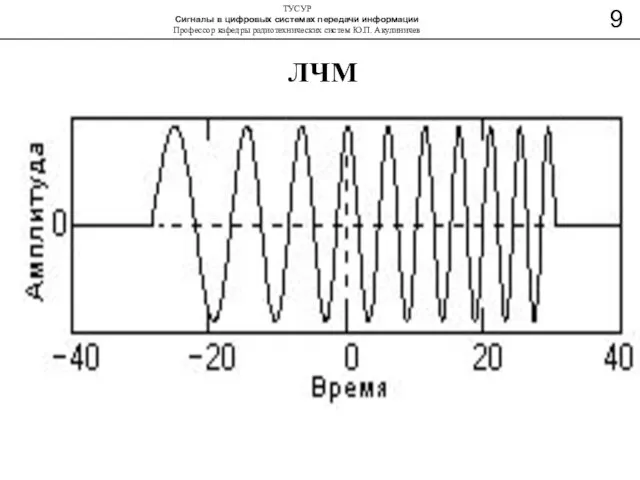
- 11. ЛЧМ
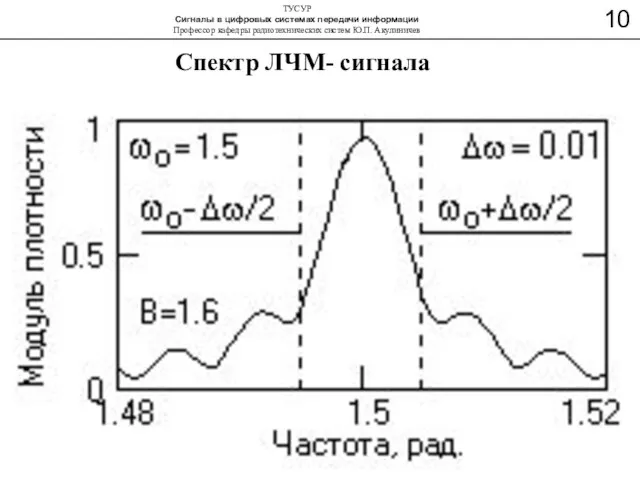
- 12. Спектр ЛЧМ- сигнала
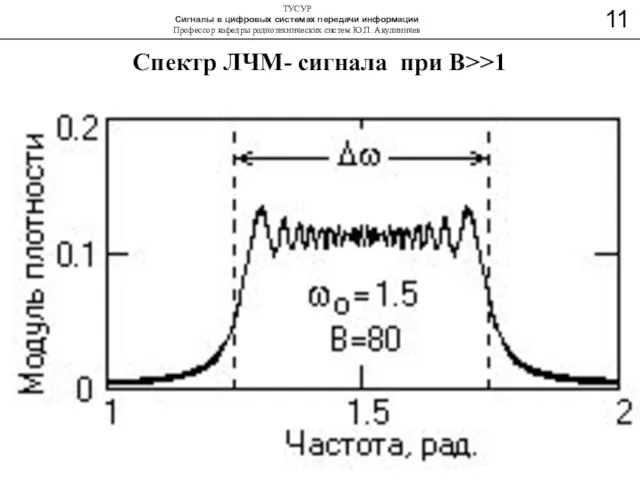
- 13. Спектр ЛЧМ- сигнала при B>>1
- 14. Цифровые сигналы Сигнал X, который может находиться лишь в одном из m возможных состояний, называется m-ичным
- 15. Цифровые сигналы Примеры: 1) Х – русская буква, m=33, её возможные значения (алфавит): а,б,…,я. Есть экспериментальные
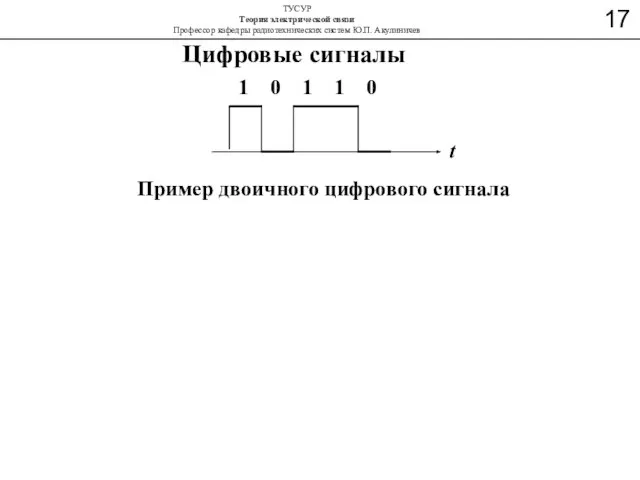
- 16. Цифровые сигналы 1 0 1 1 0 t Пример двоичного цифрового сигнала
- 17. Спектр сигнала
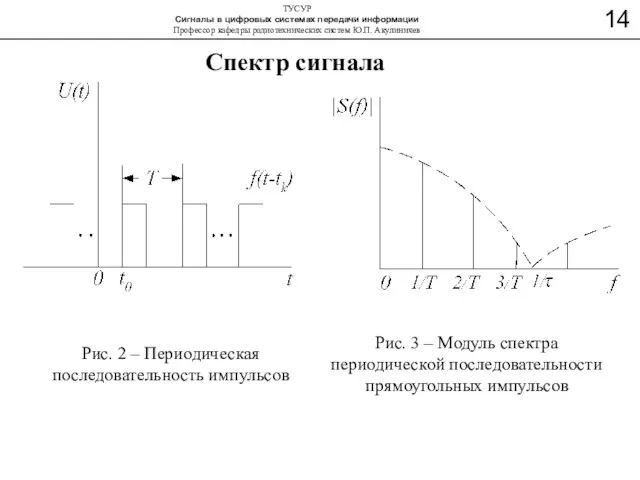
- 18. Спектр сигнала
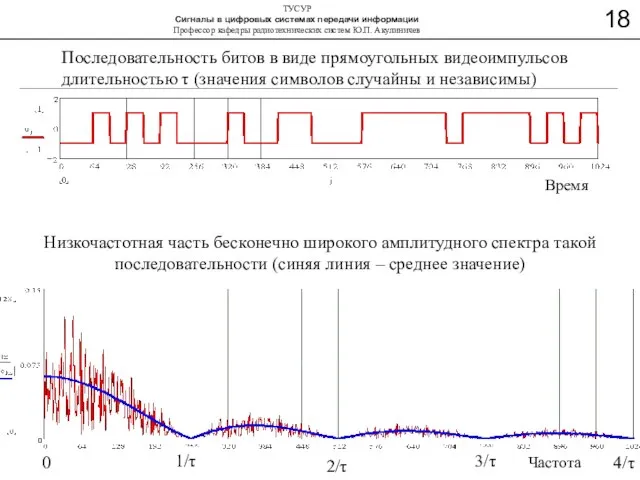
- 19. Последовательность битов в виде прямоугольных видеоимпульсов длительностью τ (значения символов случайны и независимы) Низкочастотная часть бесконечно
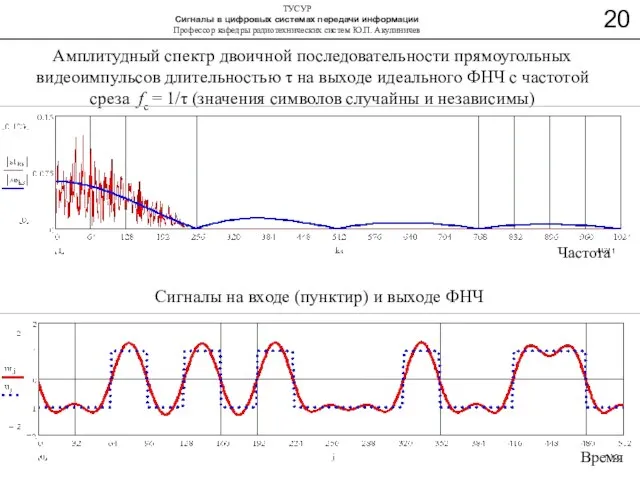
- 20. Амплитудный спектр двоичной последовательности прямоугольных видеоимпульсов длительностью τ на выходе идеального ФНЧ с частотой среза fc
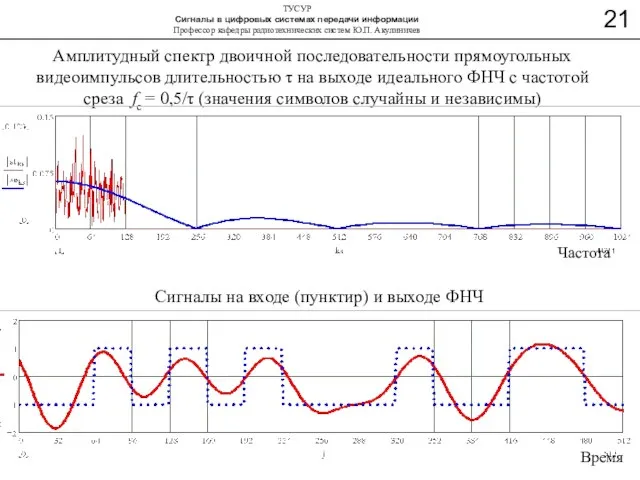
- 21. Амплитудный спектр двоичной последовательности прямоугольных видеоимпульсов длительностью τ на выходе идеального ФНЧ с частотой среза fc
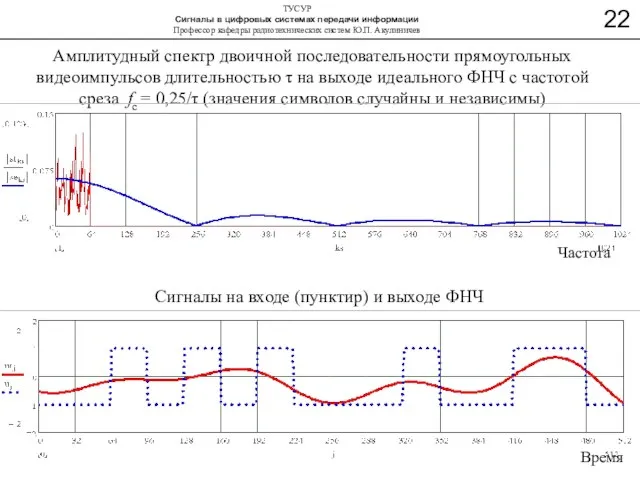
- 22. Амплитудный спектр двоичной последовательности прямоугольных видеоимпульсов длительностью τ на выходе идеального ФНЧ с частотой среза fc
- 23. Амплитудный спектр двоичной последовательности прямоугольных видеоимпульсов длительностью τ на выходе идеального ФНЧ с частотой среза fc
- 24. Важно то, что информацию содержит только случайное сообщение и случайный сигнал! Электросвязь – это связь с
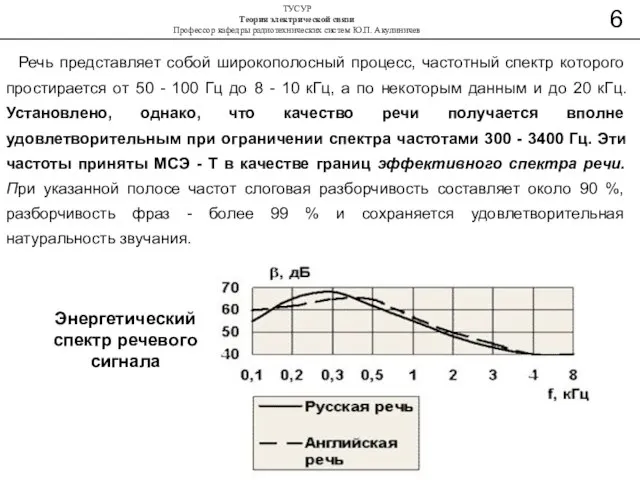
- 25. Речь представляет собой широкополосный процесс, частотный спектр которого простирается от 50 - 100 Гц до 8
- 26. Коэффициент активности телефонного сообщения, т. е. отношение времени, в течение которого мощность сигнала на выходе канала
- 27. Частотный спектр сигнала вещания расположен в полосе частот 15...20000 Гц. При передаче, как телефонного сигнала, так
- 28. Цифровой сигнал. Основным параметром цифрового сигнала с точки зрения его передачи является требуемая скорость передачи, выражаемая
- 29. Аналогичные параметры определяются и для каналов связи. Параметры каналов связи должны быть не меньше соответствующих параметров
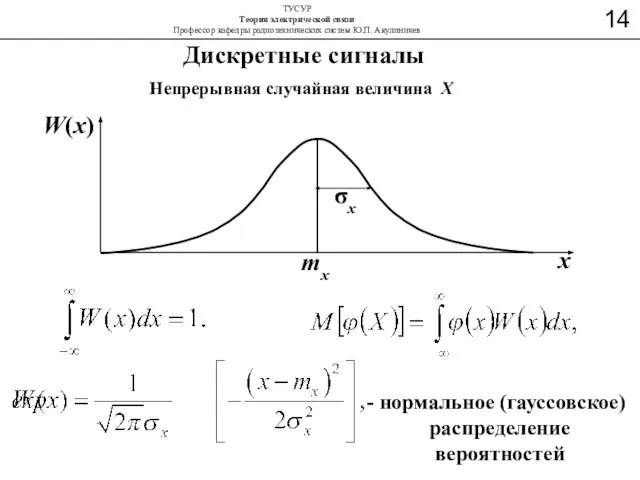
- 30. Дискретные сигналы Непрерывная случайная величина Х W(x) x mx σx нормальное (гауссовское) распределение вероятностей
- 31. Дискретные сигналы Последовательность, состоящая из n непрерывных случайных величин - совместная плотность вероятностей
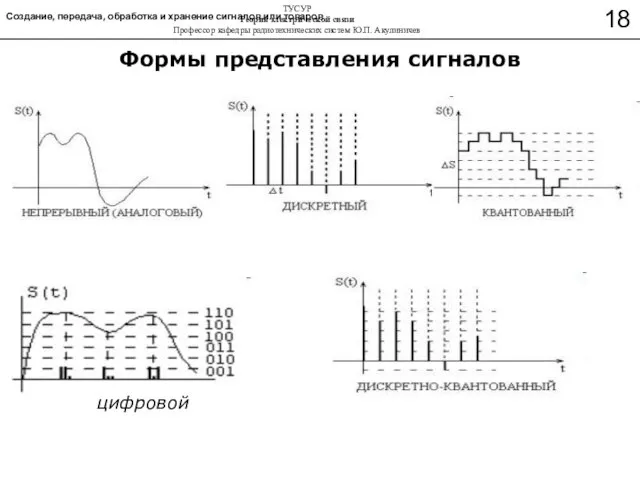
- 32. цифровой Формы представления сигналов Создание, передача, обработка и хранение сигналов или товаров
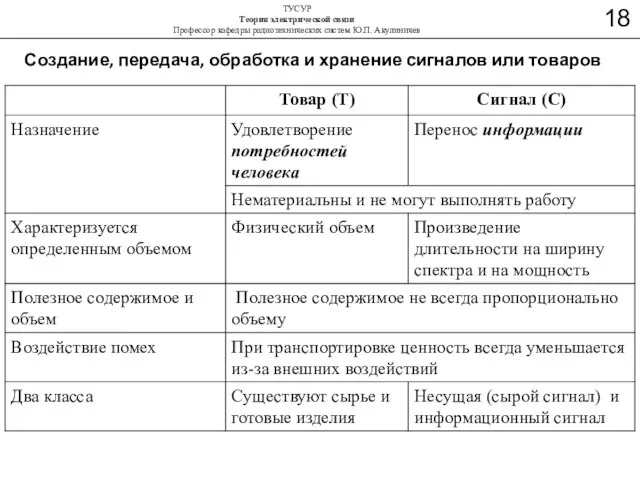
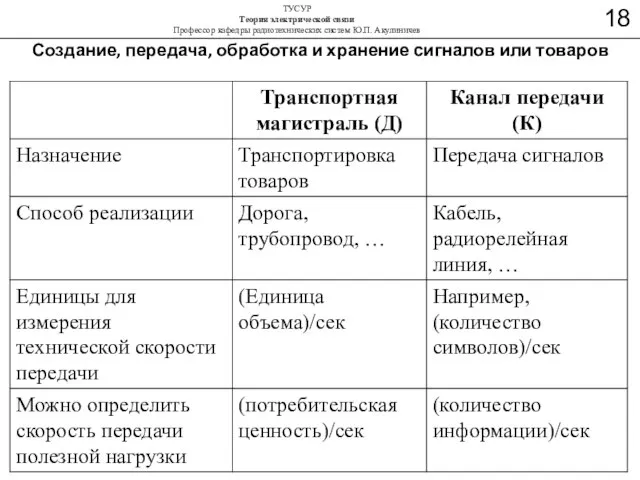
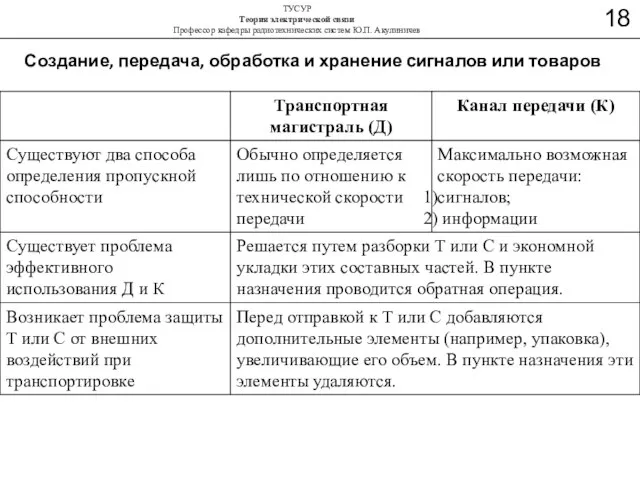
- 33. Создание, передача, обработка и хранение сигналов или товаров
- 34. Создание, передача, обработка и хранение сигналов или товаров
- 35. Создание, передача, обработка и хранение сигналов или товаров
- 36. Аддитивные и мультипликативные помехи аддитивная Модель помехи - белый шум
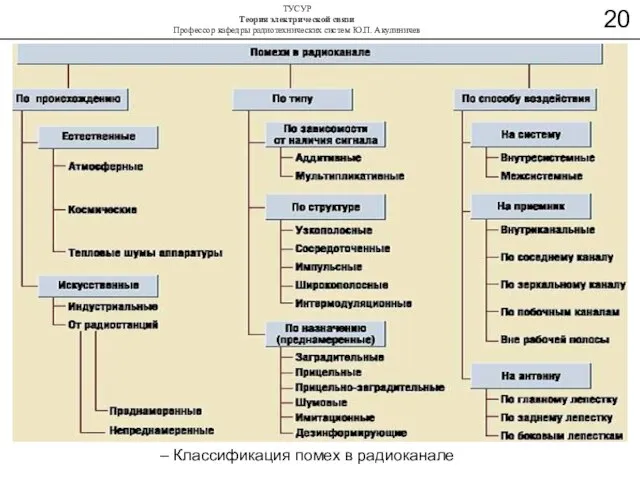
- 37. – Классификация помех в радиоканале
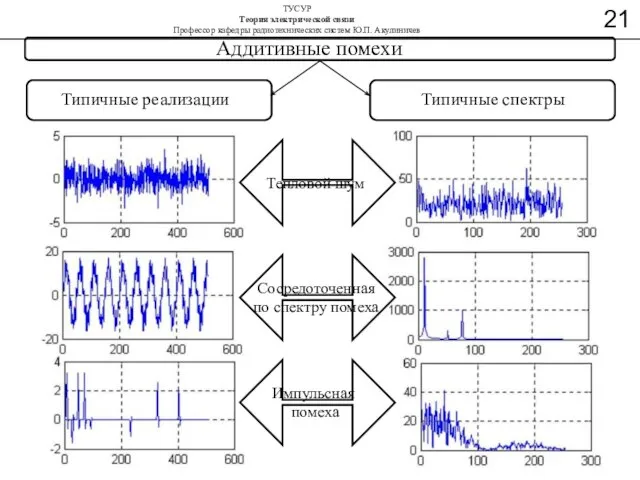
- 38. Аддитивные помехи Типичные реализации Типичные спектры Тепловой шум Сосредоточенная по спектру помеха Импульсная помеха
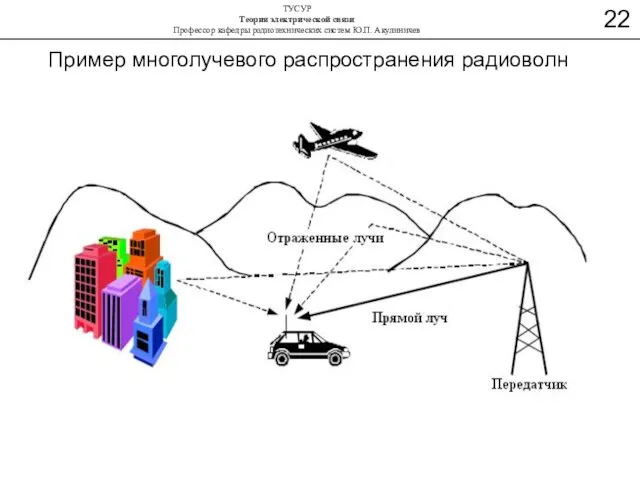
- 39. Пример многолучевого распространения радиоволн
- 40. Аддитивные и мультипликативные помехи Мультипликативная: - временные селективные замирания (фединг); - частотные селективные замирания.
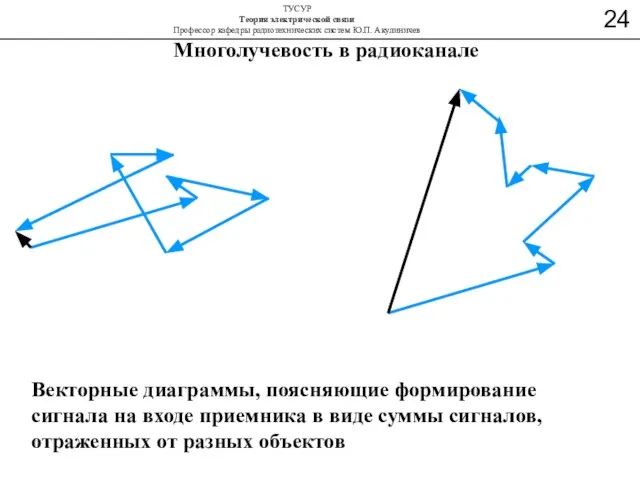
- 41. Многолучевость в радиоканале Векторные диаграммы, поясняющие формирование сигнала на входе приемника в виде суммы сигналов, отраженных
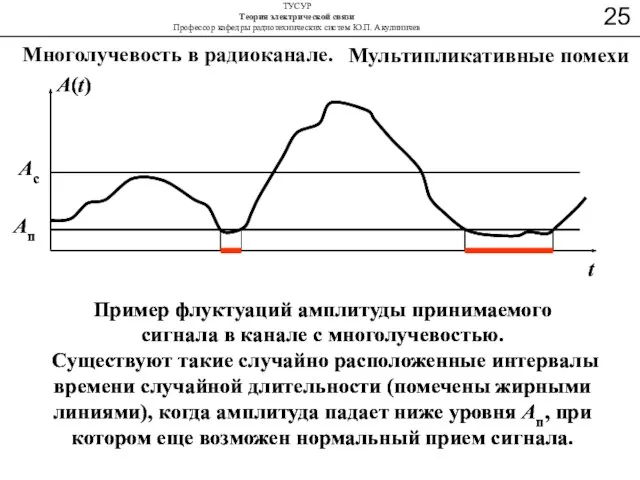
- 42. Aп Aс A(t) Пример флуктуаций амплитуды принимаемого сигнала в канале с многолучевостью. Существуют такие случайно расположенные
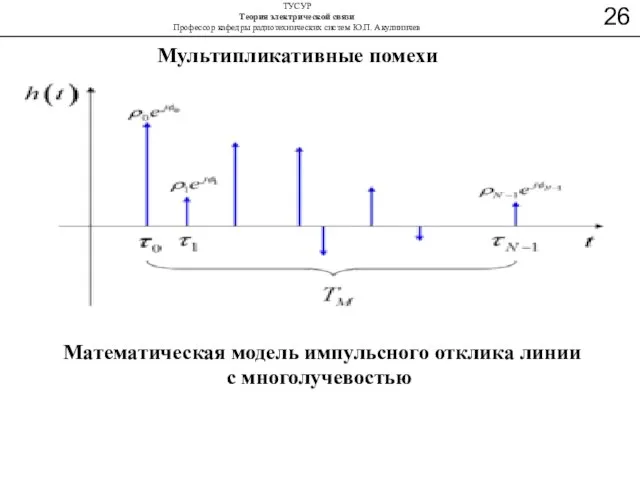
- 43. Мультипликативные помехи Математическая модель импульсного отклика линии с многолучевостью
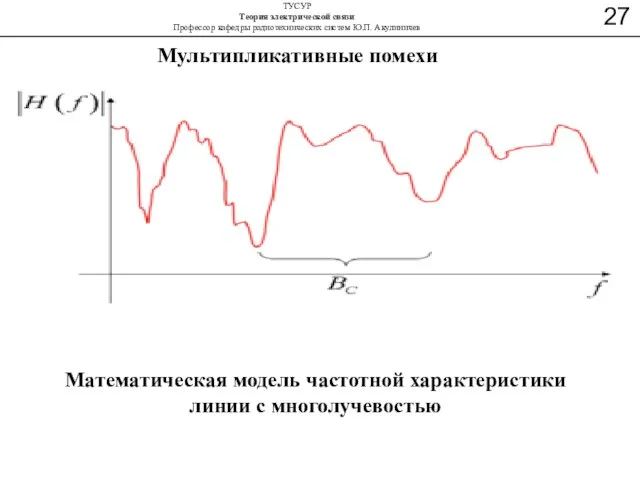
- 44. Мультипликативные помехи Математическая модель частотной характеристики линии с многолучевостью
- 45. Методы аналитического и геометрического представления сигналов и помех квадратурные составляющие - реальный сигнал
- 46. Методы аналитического и геометрического представления сигналов и помех Аналитический сигнал
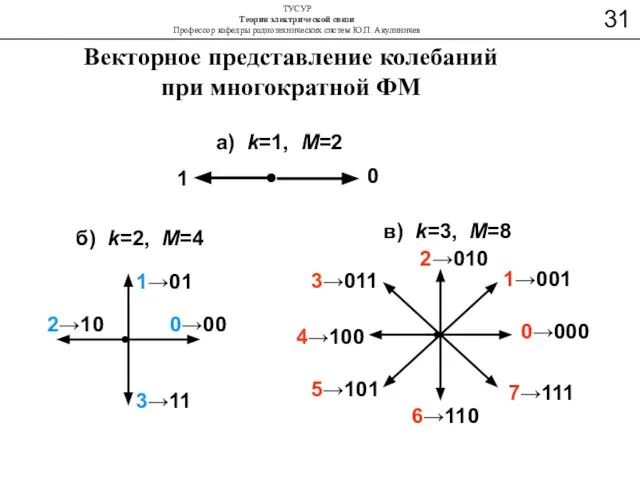
- 47. а) k=1, M=2 б) k=2, M=4 в) k=3, M=8 0→00 1→01 3→11 2→10 0→000 1→001 2→010
- 48. Геометрическое представление непрерывного сигнала в евклидовом пространстве - отсчеты с шагом Δt
- 49. Геометрическое представление непрерывного сигнала в евклидовом пространстве Расстояние между двумя непрерывными сигналами U(t) и V(t) Скалярное
- 50. Длина вектора - его вес Суммирование по модулю 2 Геометрическое представление цифрового (двоичного) сигнала в n-мерном
- 52. Скачать презентацию













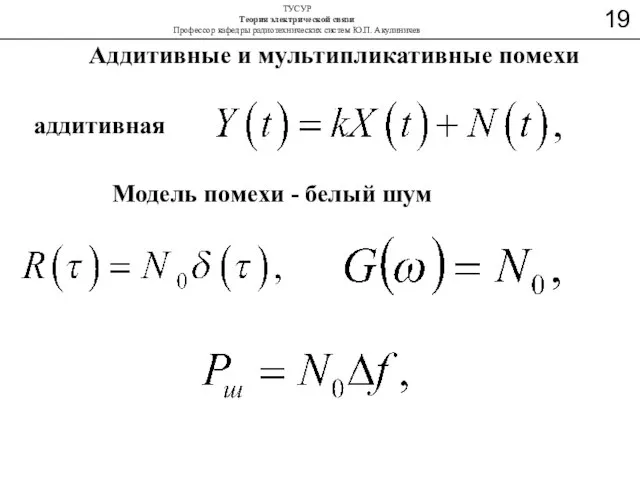






 Презентация на тему Обучение грамоте по букварю
Презентация на тему Обучение грамоте по букварю Храм книги. Необыкновенные библиотеки. Виртуальная экскурсия
Храм книги. Необыкновенные библиотеки. Виртуальная экскурсия Готовимся к ГИА
Готовимся к ГИА Чрезвычайные ситуации военного характера
Чрезвычайные ситуации военного характера Айтида Retail: Эксперт
Айтида Retail: Эксперт Вашему вниманию представляется
Вашему вниманию представляется Креативные индустрии в России: критический взгляд
Креативные индустрии в России: критический взгляд Интернет проект по дисциплине: икт в деятельности психолога
Интернет проект по дисциплине: икт в деятельности психолога Презентация на тему СИНТАКСИС И ПУНКТУАЦИЯ СЛОЖНОЕ ПРЕДЛОЖЕНИЕ 9 КЛАСС
Презентация на тему СИНТАКСИС И ПУНКТУАЦИЯ СЛОЖНОЕ ПРЕДЛОЖЕНИЕ 9 КЛАСС  "Говорит и показывает компьютер"
"Говорит и показывает компьютер" Образ российского ученого: от жалости к восхищению.
Образ российского ученого: от жалости к восхищению. Те, кто сражаются. Жизнь рыцарей
Те, кто сражаются. Жизнь рыцарей Презентация прочитанной книги
Презентация прочитанной книги Туризм: территория молодежных инноваций в рамках Всероссийского фестиваля науки 2017
Туризм: территория молодежных инноваций в рамках Всероссийского фестиваля науки 2017 Батик: история творчества, виды
Батик: история творчества, виды ВСП 1-3н
ВСП 1-3н О добром и прекрасном
О добром и прекрасном Кризис детей 3-х лет
Кризис детей 3-х лет Интерактивная игра Репка
Интерактивная игра Репка Интернет-реклама на Одноклассниках
Интернет-реклама на Одноклассниках Масляные краски
Масляные краски Презентация на тему: Вставь пропущенную букву
Презентация на тему: Вставь пропущенную букву 20140216_dolgosrochnyy_proekt_slyuzova
20140216_dolgosrochnyy_proekt_slyuzova Презентация на тему Солженицын "Матренин двор"
Презентация на тему Солженицын "Матренин двор" В семействе Ola! Daily теперь представлены 3 типа прокладок: 1.Ola! Daily – прокладки из 100% целлюлозы 2. Ola! Daily Deo – ароматизированные прокладк
В семействе Ola! Daily теперь представлены 3 типа прокладок: 1.Ola! Daily – прокладки из 100% целлюлозы 2. Ola! Daily Deo – ароматизированные прокладк Точки на прямой
Точки на прямой Физика плазмы
Физика плазмы ИНИЦИАТИВА ЕВРОПЕЙСКОГО СООБЩЕСТВА INTERREG И “EВРОПЕЙСКОЕ ТЕРРИТОРИАЛЬНОЕ СОТРУДНИЧЕСТВО” 2007-2013 Mинистерство регионального раз
ИНИЦИАТИВА ЕВРОПЕЙСКОГО СООБЩЕСТВА INTERREG И “EВРОПЕЙСКОЕ ТЕРРИТОРИАЛЬНОЕ СОТРУДНИЧЕСТВО” 2007-2013 Mинистерство регионального раз