Теория финансового портфеля

История теории финансового портфеля
Начало современной теории финансового портфеля было заложено в статье Гарри Марковица «Выбор портфеля» (1952). В этой статье была предложена математическая модель формирования оптимального портфеля ценных бумаг и были приведены методы построения таких портфелей при определенных условиях.
Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965), и было основано на понятиях систематического (рыночного) и несистематического рисков ценной бумаги.

Основные количественные характеристики отдельной рисковой ценной бумаги
При формировании оптимального портфеля ценных бумаг необходимы рыночные данные по отдельным ценным бумагам, информация о которых представлена на многочисленных информационных сайтах. Например, многие известные рыночные данные по значениям индексов и котирования многочисленных акций представлены на сайте http://www.finam.ru/analysis/.

Доходность акции (финансового инструмента)
Доходность ri-процентное изменение стоимости инвестиции в финансовые активы за определенный период времени
где Сt – цена закрытия акции ( финансового инструмента) за данный месяц, Сt-1 – цена закрытия акции ( финансового инструмента) за предыдущий месяц .
mij – является случайной величиной , i-вид бумаги, t-время.

Математическое ожидание - mi и дисперсия – σ2i доходности ценной бумаги
pk- состояние экономики, k –число возможных состояний экономики, - среднее квадратическое отклонение, определяющая риск ценной бумаги

Ковариация и корреляция между доходностями двух ценных бумаг –A и B
Ковариация-
Корреляция -,
Коэффициент вариации доходности -

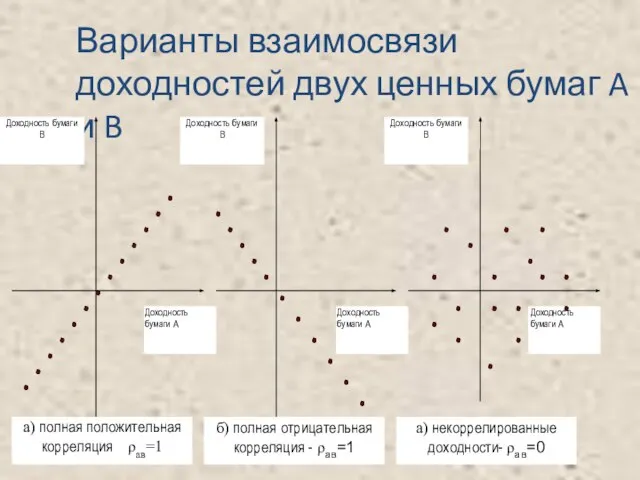
Варианты взаимосвязи доходностей двух ценных бумаг A и B

Правила доминирования рационального инвестора
1. Если m1 = m2 и σ1<σ2, то первый вид ценных бумаг предпочтительнее, поскольку с ним связана меньшая степень риска.
2. Если σ1=σ2, а m1 > m2 , то целесообразно вложить деньги в 1-й вид ценных бумаг.
3. Если m1 > m2 и σ1>σ2 или m1 < m2 и σ1<σ2 , то целесообразно использовать коэффициент вариации доходности - С
Однако в зависимости от индивидуальной склонности к риску инвестор может предпочесть вариант с большей ожидаемой доходностью, но связанной и с большим риском, либо вариант с меньшей ожидаемой доходностью, но менее рискованный.

Задача 1. Рассматриваются три равновероятных состояния экономики S1,S2,S3 , т.е. каждое состояние может реализоваться с одинаковой вероятностью pk = 1/ 3 , k = 1,2,3. Значения доходностей ценных бумаг двух компаний A и B для каждого состояния k приводятся в табл. (в процентах).
Определить :1.Ожидаемое значение доходностей ценных бумаг каждой компании ; 2. Риск, связанный с вложением в каждую ценную бумагу; 3.Степень зависимости доходностей ценных бумаг компаний А и В.

Решение
2. Дисперсии доходностей ЦБ
1.Ожидаемые доходности

Задачи формирования портфелей ценных бумаг
Портфель – это совокупность различных инвестиционных инструментов, которые собраны воедино для достижения конкретной инвестиционной цели вкладчика.
Основы теории выбора портфеля впервые были разработаны нобелевским лауреатом Гарри Марковицем в статье «Выбор портфеля», опубликованной в 1952 г. Затем в работах Вильяма Шарпа (1964) и Джона Литнера (1965), и было основано на понятиях система-тического (рыночного) и несистема-тического рисков ценной бумаги.

Задачи формирования портфелей ценных бумаг
Портфель (инвестиционный портфель) - совокупность инвестиционных инструментов.
Портфельный менеджмент – формирование инвестиционного портфеля ценных бумаг.
Главная цель в формировании портфеля – достижение оптимального сочетания между риском и доходностью за счет набора инвестиционных инструментов, который должен обеспечить:
минимум риска потерь при заданном уровне доходности;
или максимальную доходность при заданном уровне риска.

Основные характеристики портфеля ЦБ
mp- доходность портфеля ценных бумаг. Данный параметр рассчитывается как взвешенная средняя из ожидаемых доходностей по каждой из ЦБ
где xi - доли инвестиций, помещенных в каждый из видов активов (эти доли называют портфельными весами), k – вид актива. XT=(х1, х2, … хn); mk - ожидаемая доходность по каждому виду активов.

Риск портфеля
Риск портфеля - σp - стандартное отклонение ставок дохода по портфелю, рассчитывается как квадратный корень из дисперсии портфельного дохода (вариации Vp),
- ковариационная матрица порядка N.

Ковариационная матрица порядка-N
Ковариация - это статистическая мера взаимодействия двух случайных переменных, например, доходности трех ценных бумаг.
Коэффициент корреляции между двумя переменными i и j можно рассчитать по выражению

ПРИМЕР
1. Некоррелированнные ЦБ
Предположим , что ЦБ различных видов ведут себя независимо, т.е. они некоррелированы:
Тогда

Предположим, что деньги вложены равными долями во все виды ЦБ:
Тогда средняя ожидаемая доходность портфеля:
Риск портфеля:

ПРИМЕР.
Инвестор может составить портфель из
4 видов ценных бумаг:

Рассмотрим несколько вариантов составления портфеля равными долями.
1. Портфель состоит из бумаг 1 и 2 вида.

2. Портфель состоит из бумаг 1, 2 и 3 вида.

3. Портфель состоит из бумаг всех видов.
Эффективность портфеля растет быстрее, чем его риск.

При некоррелированных ЦБ, если их
число n в портфеле растет, то
риск будет ограничен и он будет
стремиться к нулю при
Уменьшение риска
портфеля за счет увеличения в нем
числа ЦБ , получил название
эффекта диверсификации.

Диверсификация
Диверсификация (разнообразие ценных бумаг в портфеле) приводит к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля, в то время как рыночный риск портфеля остается приблизительно таким же. Этот же эффект воплощен в народной мудрости – «не клади все яйца в одну корзину». Принцип диверсификации гласит, что нужно проводить разнообразные, не связанные друг с другом операции, тогда эффективность окажется усредненной, а риск однозначно уменьшится.

2. Влияние корреляции
ЦБ разного вида
Оценим влияние корреляции ЦБ.
Корреляция не влияет на эффективность портфеля, поскольку
Но она будет влиять на риск:

Рассмотрим коэффициент корреляции:
Рассмотрим два крайних случая:

2.1. Полная прямая корреляция
Это значит, что при изменении i –го фактора j – ый меняется прямо пропорционально.
Тогда

Если деньги вложить равными долями ,то
и риск портфеля составит
Однако, в этом случае диверсификация портфеля не дает эффекта – риск портфеля не будет стремиться к нулю при

Заметим, что положительная корреляция между эффективностями ЦБ имеет место, когда их курс определяется одним фактором.
Например, цены акций электрических и транспортных компаний пропорциональны цене на нефть.
Диверсификация путем покупки и тех и других акций бесполезна – риск портфеля оказывается приблизительно таким же, как и среднеквадратичное отклонение цены на нефть.

2.2. Полная обратная корреляция
Пусть n=2:

Если
То
Таким образом, при обратной корреляции возможно такое распределение вложений, при которой риск полностью отсутствует.

Эффективный инвестиционный портфель
Эффективный портфель – это портфель подверженных риску ценных бумаг (активов), дающий максимальный средний доход из всех портфелей с одинаковой дисперсией.

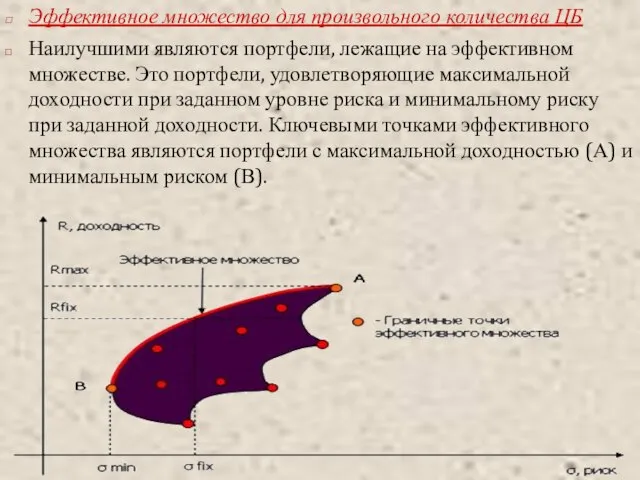
Эффективное множество для произвольного количества ЦБ
Наилучшими являются портфели, лежащие на эффективном множестве. Это портфели, удовлетворяющие максимальной доходности при заданном уровне риска и минимальному риску при заданной доходности. Ключевыми точками эффективного множества являются портфели с максимальной доходностью (А) и минимальным риском (В).

Модели оптимального портфеля
Задача оптимизации сводится к определению такой структуры состава портфеля(т.е. x1,x2,… инвестиций, чтобы величина ожидаемого дохода – mp и - уровень риска соответствовали целям инвесторов.
При этом целевой функцией может быть минимизация риска при заданной доходности, либо максимизация дохода при риске не выше заданного, a на компоненты вектора X, представляющего состав портфеля могут накладываться различные ограничения, зависящие от вида сделки, типа участвующих активов, величины открываемых позиций и т. д.

Модель Блэка
В модели Блэка допустимыми являются любые портфели, т.е. вектор Х удовлетворяет лишь основному ограничению:
.
Наличие коротких позиций (отсутствие условия неотрицательности) позволяет реализовать любую, сколь угодно большую доходность, естественно за счет большого риска.

2. Модель Марковица
Модель Марковица рассматривает в качестве допустимых только стандартные портфели (без коротких позиций). Это значит, что на вектор Х накладываются два ограничения: основное
и неотрицательности xi ≥ 0 для всех i.

Модели портфеля ценных бумаг
Портфель называют стандартным, если инвестор по каждому активу находится в длинной (long) позиции. Длинная позиция – это обычно покупка актива с намерением его последующей продажи (закрытие позиций).
Особенностью модели Марковица является то, что доходность любого стандартного портфеля не превышает наибольшей доходности активов, из которых он построен.

Модели портфеля ценных бумаг
Оптимальное решение этой задачи обозначим значком *. Если , то это означает рекомендацию вложить долю наличного капитала в ценные бумаги i-ro вида. Если же
, то содержательно это означает провести операцию «short sale» («короткая продажа»).

Операция «short sale»
Инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги i-го вида (вместе с доходом, какой они принесли бы их владельцу за это время). За это сейчас он получает их денежный эквивалент. Эти деньги он присоединяет к своему капиталу и покупает рекомендуемые оптимальным решением ценные бумаги. Так как ценные бумаги других видов (т.е. не i-ro вида) более эффективны, то инвестор оказывается в выигрыше. Можно обойтись и без операции «short sale», если инвестору доступны займы денежных средств по безрисковой ставке.

В модели Марковица обычно рассматриваются два типа задач оптимизации портфелей: 1.Минимального риска при заданном уровне доходности;
2. Максимальной доходности при уровне риска не превышающем заданного значения.

1.Портфель Марковица минимального риска.
Найти вектор X* распределения исходного капитала, минимизирующий риск (вариацию) портфеля
при заданной эффективности портфеля
и условии, что сумма долей активов в портфеле должна составлять единицу

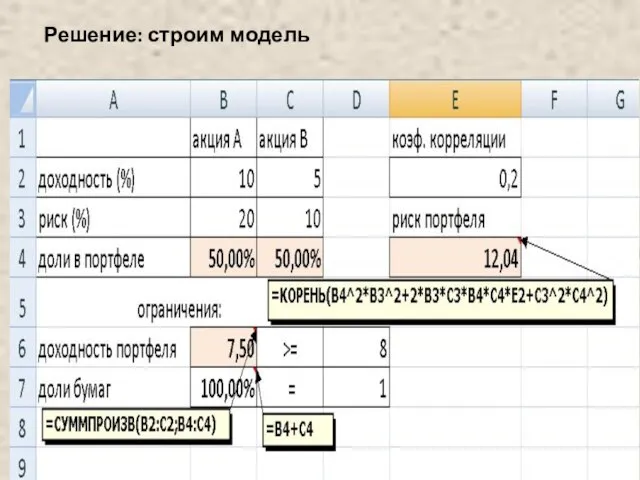
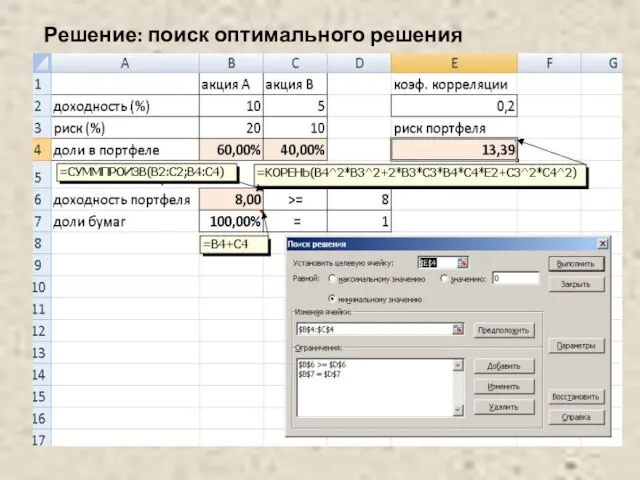
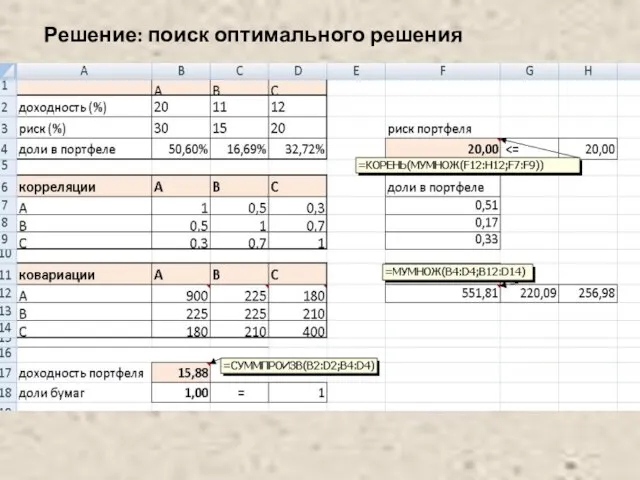
Пример
Сформировать портфель минимального риска из двух видов ценных бумаг - А с доходностью 10% и риском 20% и В с доходностью 5% и риском 10% при условии, что обеспечивается доходность портфеля не менее 8%. Коэффициент корреляции равен 0.2.
Решение.
Модель Марковица может быть сформулирована следующим образом.
Необходимо найти вектор Х= (X1, X2), минимизирующий риск портфеля σp.

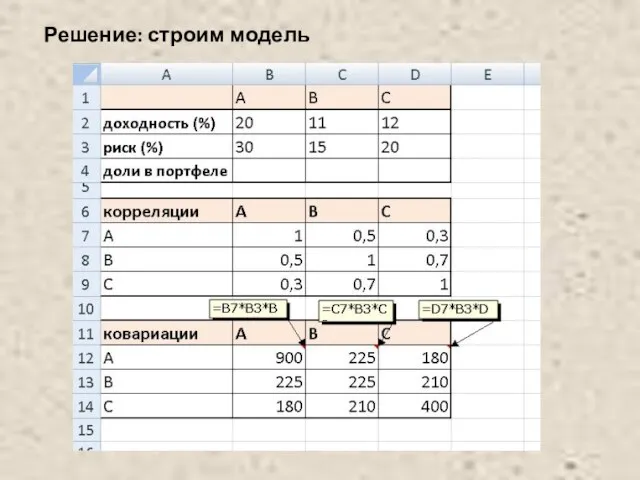
Решение: строим модель

Решение: поиск оптимального решения

2.Портфель Марковица максимальной эффективности.
Найти вектор X*, максимизирующий ожидаемую эффективность портфеля
при уровне риска не превышающем заданного значения
и условии, что сумма долей активов в портфеле должна составлять единицу

Пример.

Решение: строим модель

Решение: поиск оптимального решения

Модель Тобина-Шарпа-Литнера
(D. Tobin – также впоследствии лауреат Нобелевской премии)
В этой модели предполагается наличие так назывемых безрисковых активов, доходность которых не зависит от состояния рынка и имеет постоянное значение.
Пусть mо – эффективность безрисковых бумаг, а x0 – доля капитала, в них вложенного, тогда в рисковую часть портфеля вложена (1- x0) часть всего капитала. Пусть mr – эффективность и Vr – вариация (дисперсия) рисковой части портфеля, и – риск этой рисковой части.

Модель Тобина-Шарпа-Литнера
Эффективность всего портфеля равна
Вариация портфеля равна:
Риск портфеля:
После преобразований получим

Модель Тобина-Шарпа-Литнера
Считается, что безрисковые бумаги не коррелированны с остальными.
Эффективность портфеля линейно зависит от его риска:

3.Модель c N рисковыми бумагами Тобина
Модель Тобина –комбинированный портфель включающий , как рисковые , так и безрисковые ценные бумаги с гарантированной доходностью – mf и долей xo.
Найти вектор X* распределения исходного капитала, минимизирующий риск (вариацию) портфеля
при заданной эффективности портфеля и условии, что сумма долей активов в портфеле должна составлять единицу
и

Выводы
Современная портфельная теория основывается на допущении, что инвесторы имеют возможность распределять богатство среди множества доступных направлений инвестирования, - то есть формировать инвестиционный портфель. Причем критериями оценки эффективности инвестиционных решений являются только два параметра - ожидаемая доходность и стандартное отклонение доходности.
Эффект диверсификации состоит в возможности снижения риска инвестирования (без ущерба для доходности) путем распределения инвестиций среди доступных направлений. Чем больше степень диверсификации и чем меньше корреляция между доходностью выбранных финансовых активов - тем большими являются возможности по снижению риска.