Теория и применение радиолокационных сигналов. Лекция 05

Фазовая (фазокодовая) манипуляция (ФКМ) позволяет расширить амплитудно-частотного спектр сигнала, что улучшает разрешающую способность по дальности.
Сигнал представляет собой совокупность сомкнутых радиоимпульсов (дискрет) с общей частотой несущей f0 и одинаковыми длительностями τд, начальная фаза в каждом дискрете выбирается из совокупности возможных сдвигов фаз φq (q = 0,1,…,p-1) относительно опорного колебания.
Структуру сигнала обычно записывают в виде цифровой последовательности, элементы которой принадлежат системе счисления размерности p.
Начальные фазы обычно равномерно распределены на интервале [0; 2π], но встречается и неравномерное распределение. Для равномерного распределения начальные фазы имеют вид:
Фазокодоманимулированный сигнал

Наиболее распространенны в локации являются ФКМ, использующие двоичный код (p = 2):
код Баркера;
М-последовательность;
коды Голда.
В системах связи наиболее распространены:
коды Уолша;
коды Голда;
коды Касами.
Выражение для комплексной огибающей ФКМ импульса можно представить в виде:
Применяемые коды для ФКМ сигналов

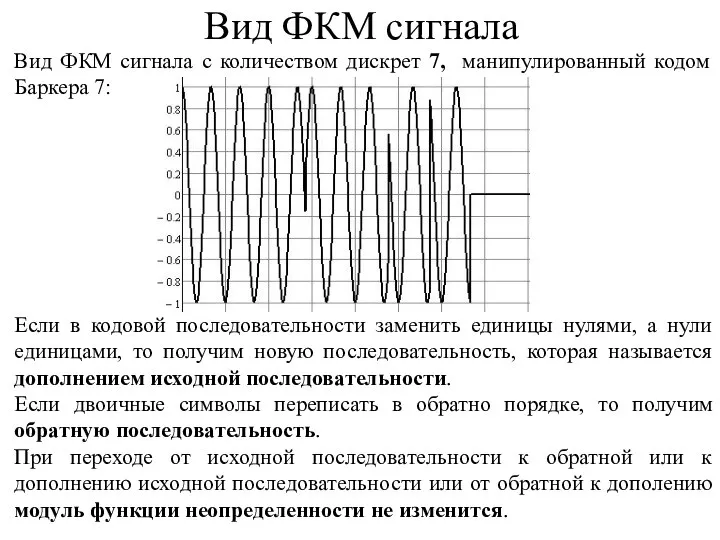
Вид ФКМ сигнала с количеством дискрет 7, манипулированный кодом Баркера 7:
Если в кодовой последовательности заменить единицы нулями, а нули единицами, то получим новую последовательность, которая называется дополнением исходной последовательности.
Если двоичные символы переписать в обратно порядке, то получим обратную последовательность.
При переходе от исходной последовательности к обратной или к дополнению исходной последовательности или от обратной к дополению модуль функции неопределенности не изменится.
Вид ФКМ сигнала

Постулаты Голомба
В псевдослучайной последовательности количество нулей и единиц должно отличаться не более чем на 1.
В каждом периоде последовательности половина серий (последовательных одинаковых символов) должна иметь длину один, четверть серий - должна иметь длину два, одна восьмая должна иметь длину три и т.д., для каждой из этих длин должно быть одинаковое количество серий из "1" и "0".
Автокорреляционная функция псевдослучайной последовательности должна иметь при рассогласовании на целое число дискретов не более двух ненулевых значений (единица и уровень бокового лепестка).
Выполнение этих постулатов обычно не обеспечивается, большинство кодов не могут удовлетворить третьему постулату, соответственно большинство кодов – являются квазипсевдослучайной последовательностью, однако приставку «квази-» часто опускают.

Код Баркера
Табличный код, эвристический, постулатам Голомба не подчиняется, уровень боковых лепестков тела ρ(τ, F) в сечении F = 0 при двоичной манипуляции с начальными фазами 0; π составляет 1/nд, где nд – количество дискрет в сигнале.
В настоящее время подобраны такие коды для nд ≤13. Начальная фаза 0 описывается кодом 0, начальная фаза π описывается кодом 1.

М-последовательность
Псевдослучайный код, 3 постулату при использовании в пределах периода не обеспечивает, однако обеспечивает выполнение при непрерывном излучении в качестве периодического кода.
Период повторения 2m-1, определяется длиной задающего полинома m.
Существует два рекуррентных метода синтеза кода:
В первом методе начальные значения последовательности могут быть любыми но не все одинаковые.
Задающий полином (в обоих методах) должен иметь ненулевой член при старшей степени и не иметь внутренней периодичности

Код Голда
Псевдослучайный код, 3 постулат не обеспечивает, так как имеет не менее 3х ненулевых значения в ВКФ и АКФ, применяется в основном для синтеза групп кодов для создания квазиортогональных созвездий сигналов.
Период повторения 2m-1, определяется длиной задающего полинома m, количество синтезируемых кодов 2m+1.
Для синтеза кода Голда требуется:
две М-последовательности с различными задающими полиномами;
выбрать взаимное смещение между последовательностями, в пределах одного периода.
Полученный код Голда имеет тот же период повторения что и родительские последовательности.

Код Уолша
В основном используется за счет прекрасной взаимной корреляционной функции.
Основное достоинство – различие между кодами в группе составляет половину длины кода.
Синтез кода Уолша рекурентный, на основе матрицы Адамара:
В основном используется как расширяющий код, то есть для разделения абонентов, либо для обеспечения высокостабильной связи, так как размер группы невелик относительно передаваемого объема информации.

Код Касами
Применяется как альтернатива кодам Голда, так как позволяет изменять размер кода практически не нарушая постулаты Голомба.
Для синтеза используется 2 М-последовательности с разным периодом повторения:
При синтезе начальные полиномы для М-последовательностей выбираются таким образом, чтобы последовательности были не коррелированы.
Синтез в значительной мере эвристическая задача, выбранные смещения последовательностей влияют на свойства кода Касами. Взаимная корреляционная функция требует смещения между кодами созвездия не менее чем на N.

В общем случае ФН ФКМ сигнала имеет вид:
ФН одиночного ФКМ импульса

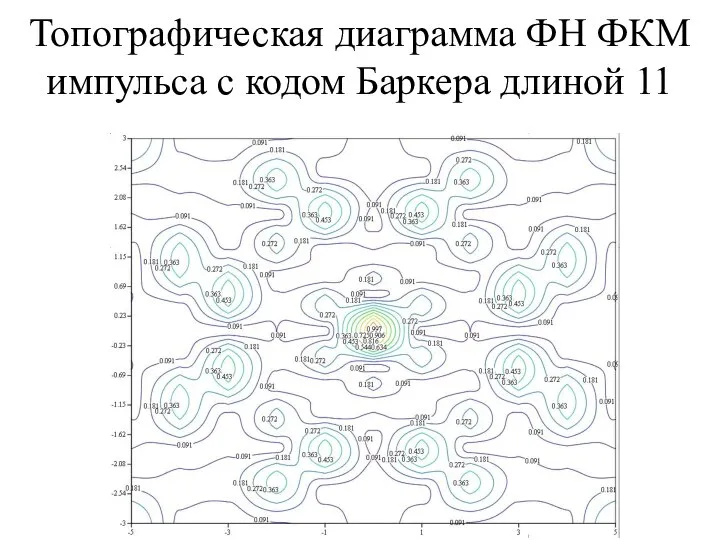
Топографическая диаграмма ФН ФКМ импульса с кодом Баркера длиной 11

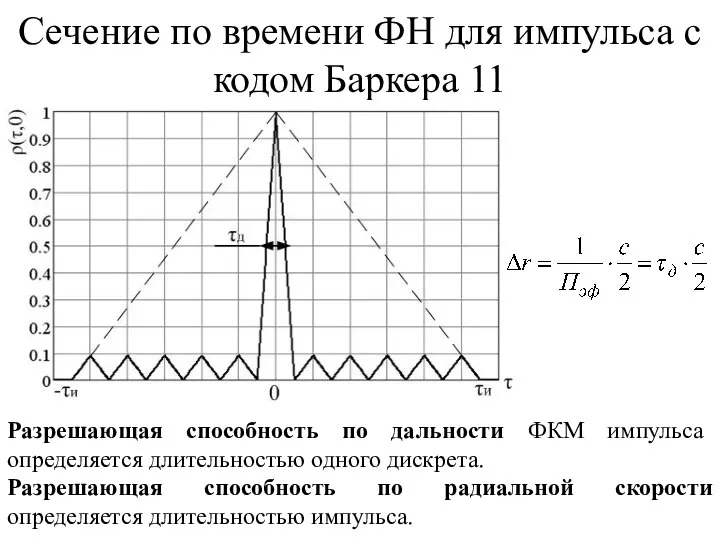
Сечение по времени ФН для импульса с кодом Баркера 11
Разрешающая способность по дальности ФКМ импульса определяется длительностью одного дискрета.
Разрешающая способность по радиальной скорости определяется длительностью импульса.

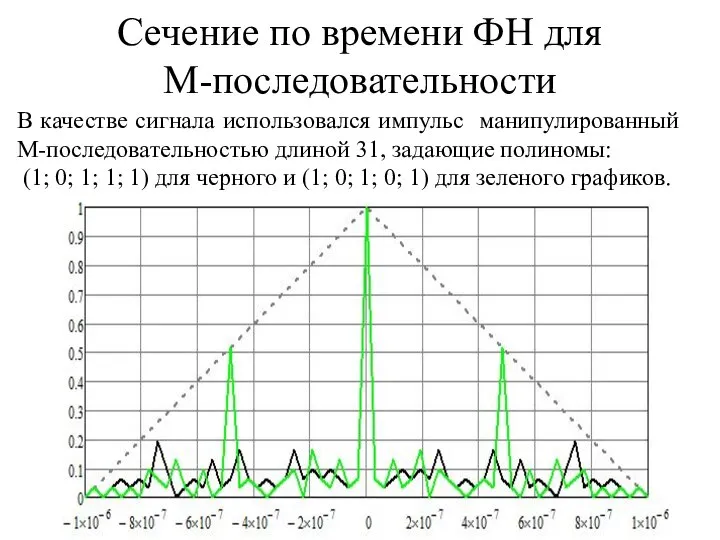
Сечение по времени ФН для
М-последовательности
В качестве сигнала использовался импульс манипулированный М-последовательностью длиной 31, задающие полиномы:
(1; 0; 1; 1; 1) для черного и (1; 0; 1; 0; 1) для зеленого графиков.

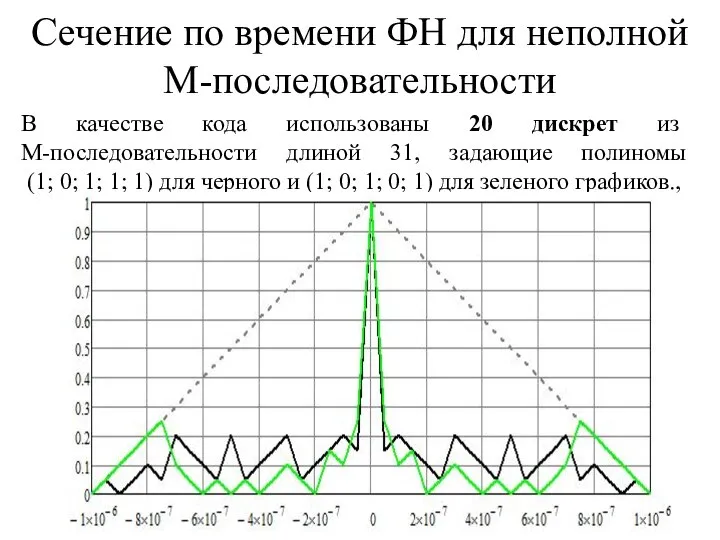
Сечение по времени ФН для неполной М-последовательности
В качестве кода использованы 20 дискрет из
М-последовательности длиной 31, задающие полиномы
(1; 0; 1; 1; 1) для черного и (1; 0; 1; 0; 1) для зеленого графиков.,

Свойства ФН ФКМ сигнала
Независимо от кода, функция неопределенности ФКМ сигнала обладает осевой и центральной симметрией.
Предсказать поведение боковых лепестков при рассогласовании по времени и частоте достаточно сложно, но их уровень не превышает указанных максимальных значений.
Также независимо от кода сечение по оси частот ФКМ импульса соответствует выражению sin(x)/x и соответствует сечению немодулированного сигнала с той же длиной импульса, аналогичным образом ведет себе сечение по частоте для пачечного ФКМ сигнала.
Применение весовой обработки для пачечного сигнала допустимо только по частоте.
Запрет применения весовых окон для импульса или непрерывного участка кода обусловлен нарушением постулатов Голомба, так как вес каждого дискрета в последовательности будет искажаться.

Задачи