Содержание
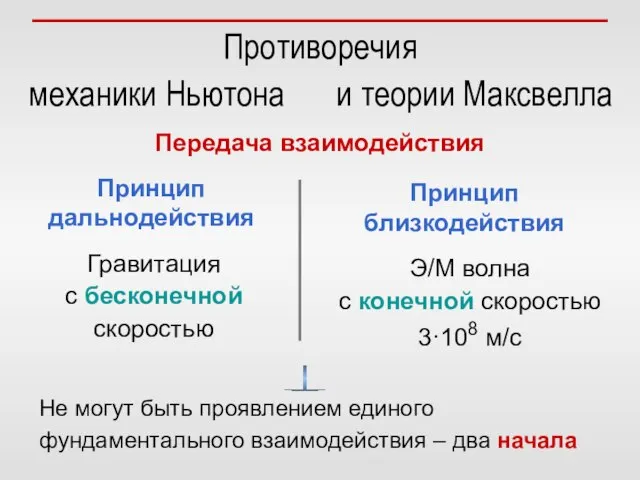
- 2. Противоречия механики Ньютона и теории Максвелла Принцип близкодействия Принцип дальнодействия Гравитация с бесконечной скоростью Э/М волна
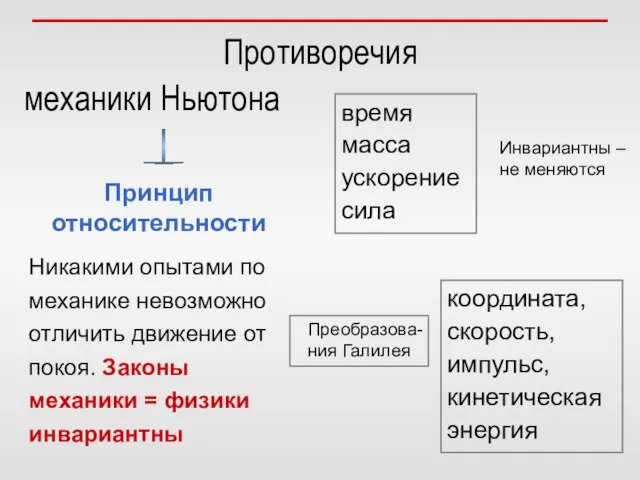
- 3. Противоречия механики Ньютона и теории Максвелла Принцип относительности Никакими опытами по механике невозможно отличить движение от
- 4. Противоречия механики Ньютона Принцип относительности Никакими опытами по механике невозможно отличить движение от покоя. Законы механики
- 5. Противоречия механики Ньютона и теории Максвелла Законы меняют свой вид в разных СО Неинвариантны Принцип относительности
- 6. Теория относительности специальная общая Для ИНЕРЦИАЛЬНЫХ систем отсчета Распространяется на НЕИНЕРЦИАЛЬНЫЕ систем отсчета Принципы 1. Относительности
- 7. Хендрик Антон Лоренц (1853 – 1928) 1904 Преобразования Лоренца
- 8. Альберт Эйнштейн (1879-1955) 1905 «К электродинамике движущихся тел».
- 9. Эйнштейн не отказывается от принципа относительности Галилея Наоборот, он делает его более общим – распространяет и
- 10. Откуда взялся постулат о постоянстве скорости света? Из теории – уравнений Максвелла Из проверки экспериментами Майкельсон-Морли
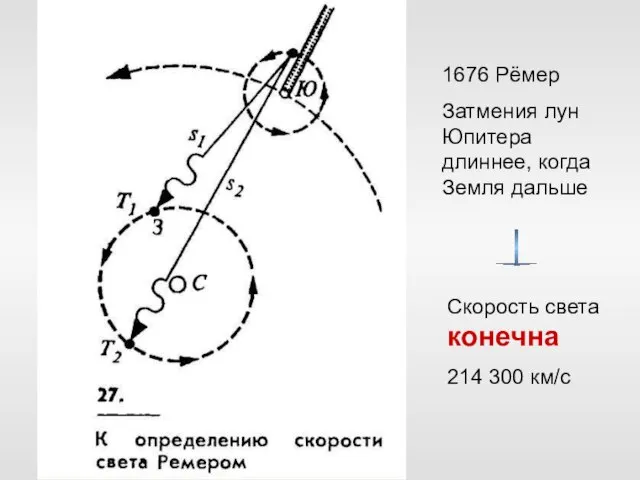
- 11. 1676 Рёмер Затмения лун Юпитера длиннее, когда Земля дальше Скорость света конечна 214 300 км/с
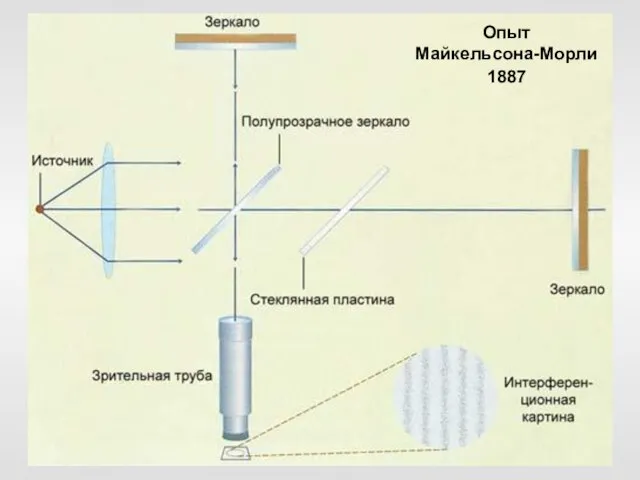
- 12. Опыт Майкельсона-Морли 1887
- 13. «Каждый луч света движется в «покоящейся» системе координат с определенной скоростью с, независимо от того, испускается
- 14. одновременно 1 2 одновременно С точки зрения В2 для В1 – неодновременно в 2 раньше, чем
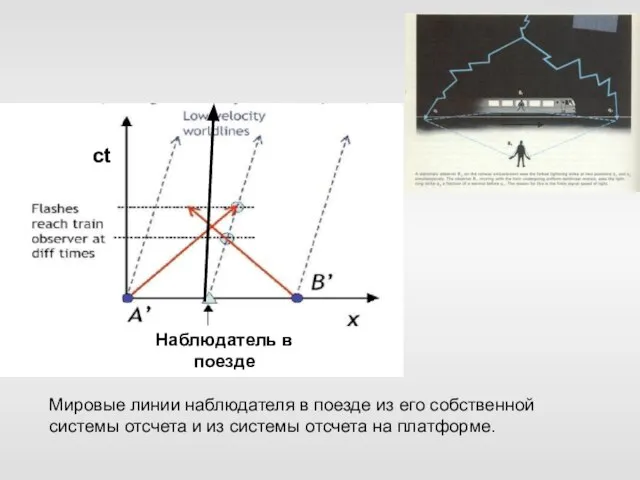
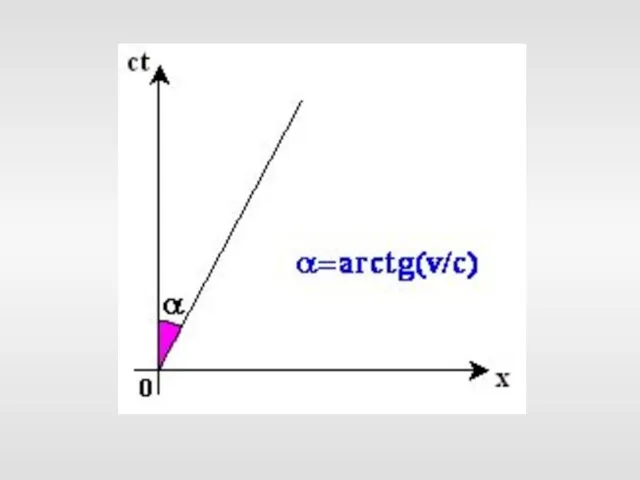
- 15. ct Наблюдатель в поезде Мировые линии наблюдателя в поезде из его собственной системы отсчета и из
- 16. Событие вместо материальной точки Центральное понятие СТО – событие Описывается 4 координатами в каждой системе отсчета
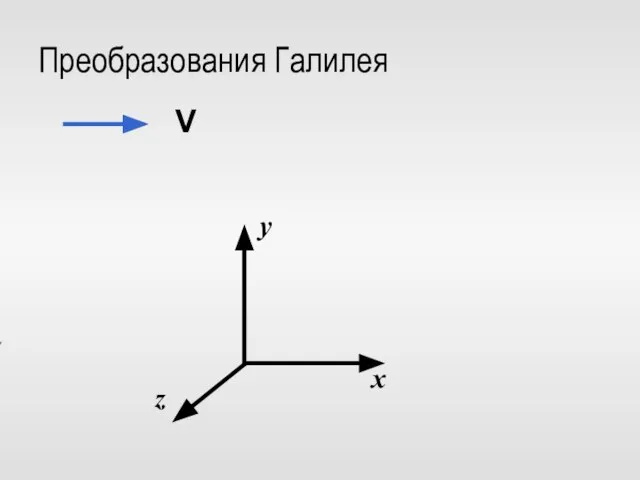
- 17. Преобразования Галилея V
- 18. Для события в точке P: в K P = (x, y, z, t) в K’ P
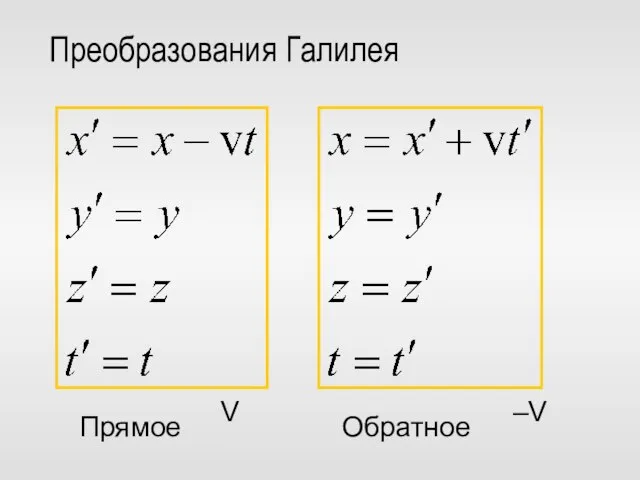
- 19. Преобразования Галилея Прямое Обратное V –V
- 20. Вывод преобразований Лоренца Должны быть линейны (следует из однородности пространства) Введем коэффициент x = x' +
- 21. Вывод преобразований Лоренца Пусть в момент 0 начала координат К и К´ совпадают. Из точки 0
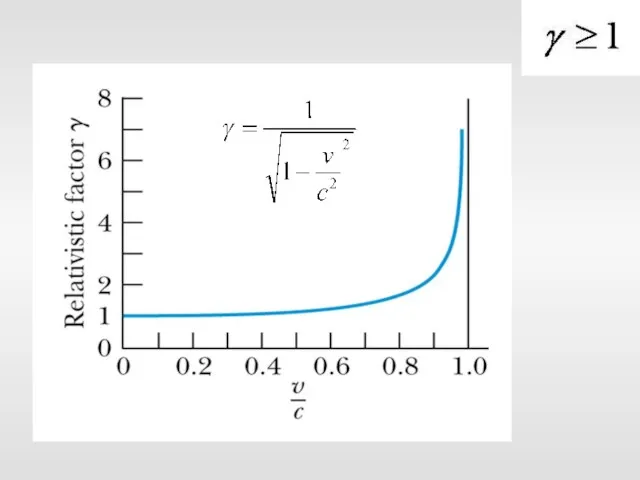
- 22. Преобразования Лоренца Релятивистский коэффициент Всегда > 1
- 23. Преобразования Лоренца
- 24. Преобразования Лоренца Релятивистский коэффициент
- 26. v Иначе γ будет мнимым, что лишено физического смысла Таким образом, вывод о том, что любая
- 27. Это ограничение верно не только для движущихся объектов, но и для сигналов. Если мы принимаем принцип
- 28. Следствия преобразований Лоренца
- 29. Замедление времени = часы в К´ идут медленней – с точки зрения К В движущейся системе
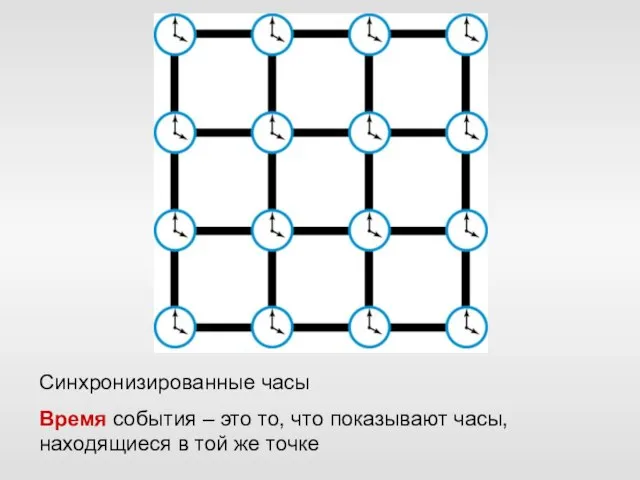
- 30. Синхронизированные часы Время события – это то, что показывают часы, находящиеся в той же точке
- 31. Собственное время Та же точка Время между двумя событиями в одном месте, измеренное часами, находящимися в
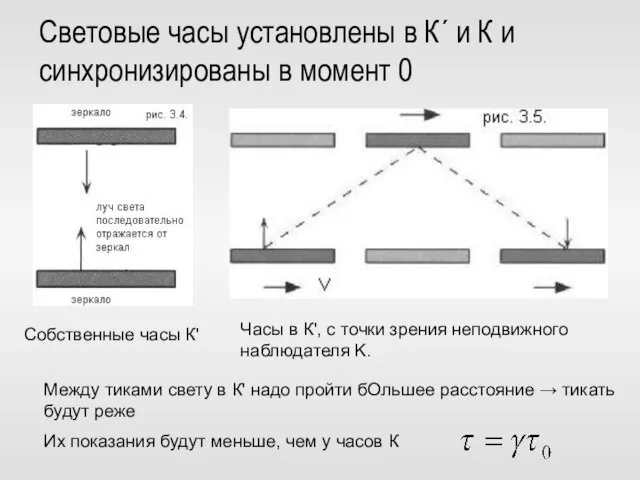
- 32. Световые часы установлены в К´ и К и синхронизированы в момент 0 Часы в К', с
- 33. Для наблюдателя, летящего в К´ то же будет казаться относительно часов, неподвижно установленных в К –
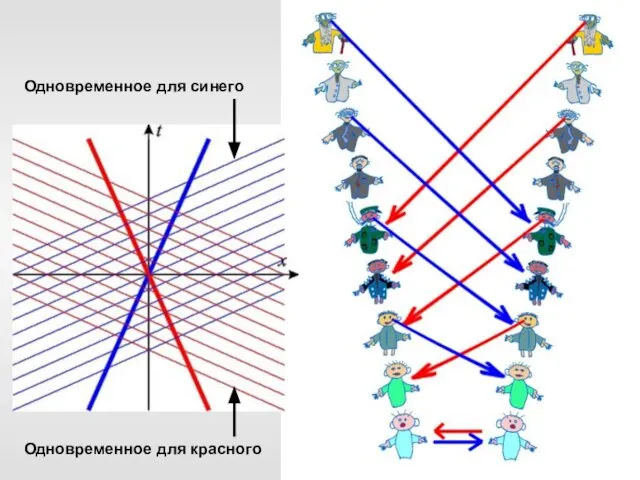
- 34. Одновременное для красного Одновременное для синего
- 35. Экспериментальное подтверждение замедления времени
- 36. В 1935 году во вторичных космических лучах, рождающихся при столкновении первичных космических частиц с молекулами воздуха
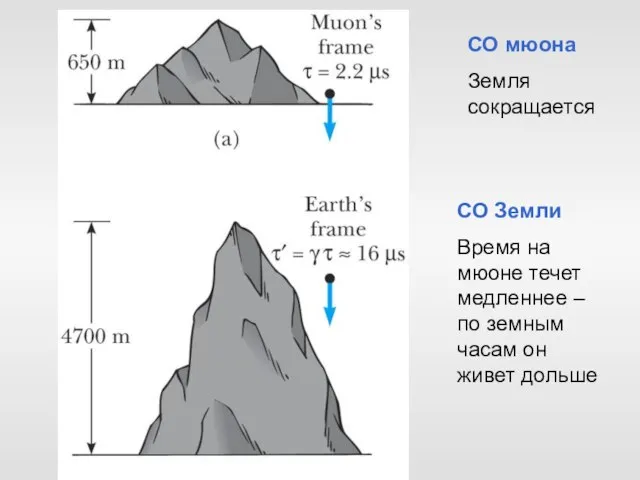
- 37. СО мюона Земля сокращается СО Земли Время на мюоне течет медленнее – по земным часам он
- 38. Укорочение отрезков Собственная длина L0 – измеренная линейкой в системе отсчета, где отрезок неподвижен. 1. Можно
- 39. Укорочение отрезков Собственная длина L0 – измеренная линейкой в системе отсчета, где отрезок неподвижен. Тот же
- 40. Сложение скоростей K′ движется относительно К со скоростью V, а в K′ со скоростью u' движется
- 41. Для случая, когда u‘ параллельна оси X Следствие: при сложении любых двух скоростей V и u',
- 42. V = с – χ u' = с – λ Подставим Если обе скорости V и
- 43. Графическое изображение преобразований – мир Минковского Герман Минковский 1864 — 1909 4-мерное псевдоевклидово пространство-время
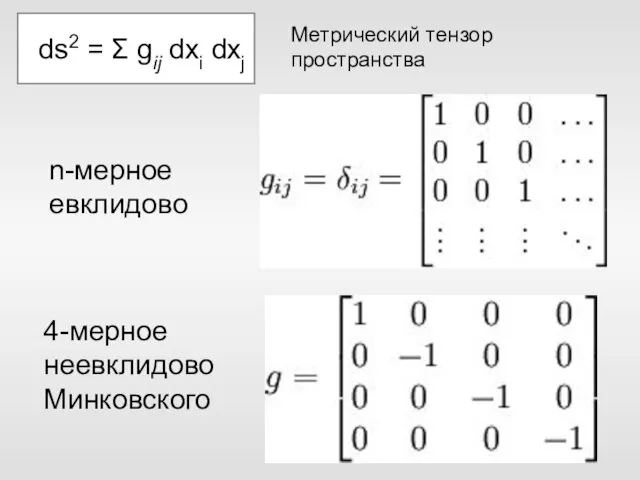
- 44. ds2 = Σ gij dxi dxj Метрический тензор пространства n-мерное евклидово 4-мерное неевклидовоМинковского
- 45. Интервал между событиями Инвариантен относительно преобразований Лоренца
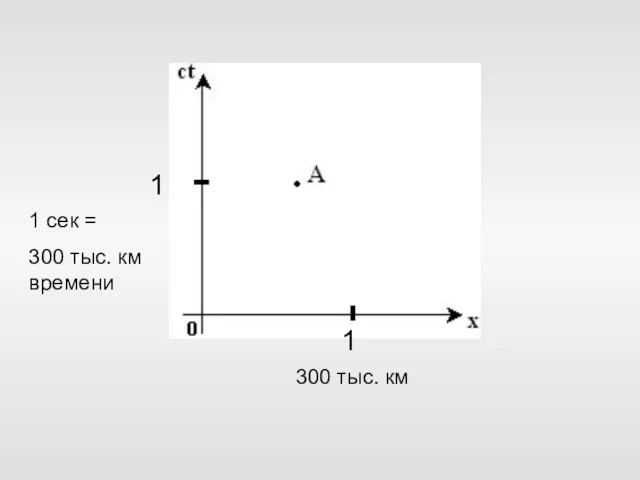
- 46. 1 1 1 сек = 300 тыс. км времени 300 тыс. км
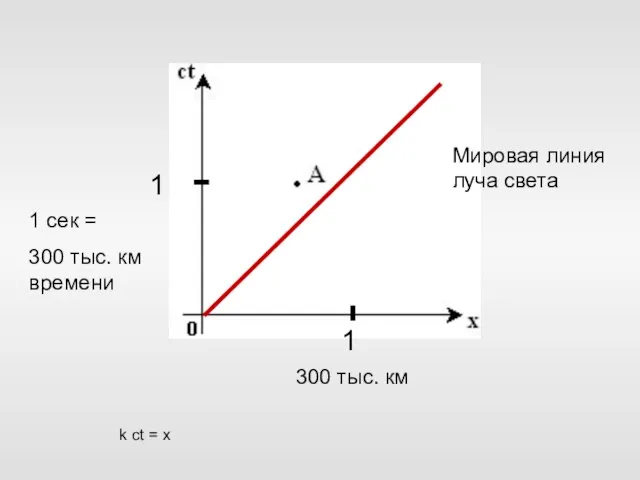
- 47. 1 1 1 сек = 300 тыс. км времени 300 тыс. км Мировая линия луча света
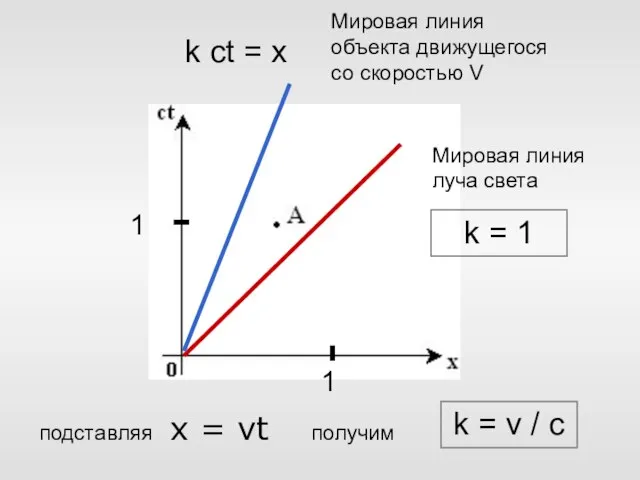
- 48. k ct = x k = v / c x = vt подставляя получим Мировая линия
- 50. s2 = c2t2 – l2 = c2t2 – (ct)2 = 0 Для событий, разделенных лучом света,
- 51. http://physics-vargin.net/books/popul/vselennaya/greene.rar
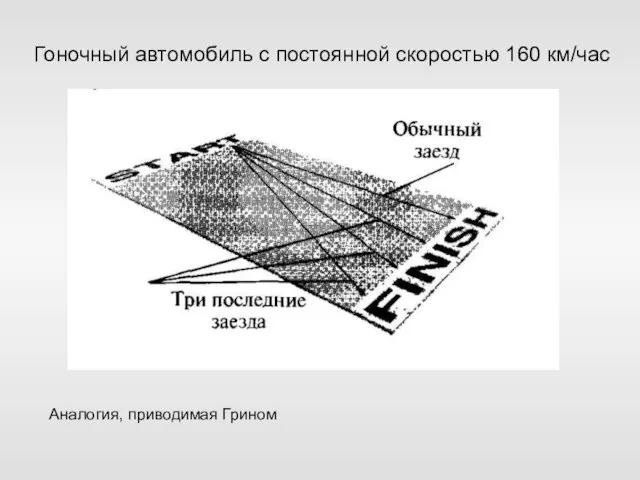
- 52. Гоночный автомобиль с постоянной скоростью 160 км/час Аналогия, приводимая Грином
- 53. Точно та же идея — разделение движения между различными измерениями — лежит в основе всех замечательных
- 54. Можем ли мы говорить о скорости движения объекта во времени подобно тому, как мы говорим о
- 55. отсюда немедленно следует факт существования ограничения на скорость тела в пространстве: максимально возможная скорость движения в
- 56. Физический смысл значения интервала для двух событий
- 57. с2t2 > R2 и s2 > 0 с2t2 с2t2 = R2 и s2 = 0 Пространственно-подобные
- 58. с2t2 > R2 и s2 > 0 Времени-подобные Существует СО, в которой события А и В
- 59. В этой СО s2 = – ΔR2 где ΔR – расстояние между точками, где произошли события,
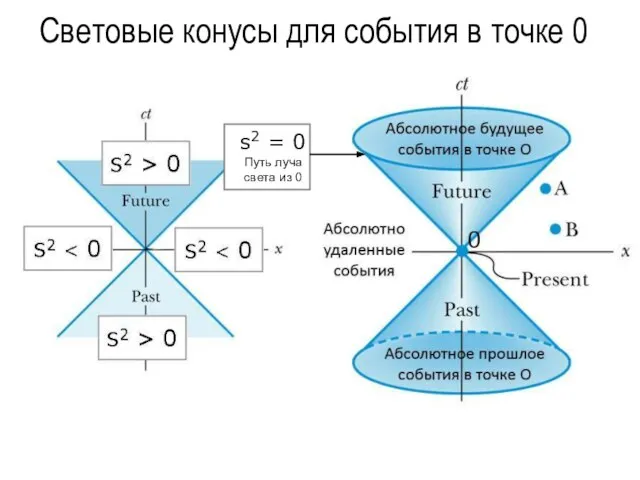
- 60. Свето-подобные Все события, лежащие на пути луча света. с2t2 = R2 и s2 = 0
- 61. Световые конусы для события в точке 0
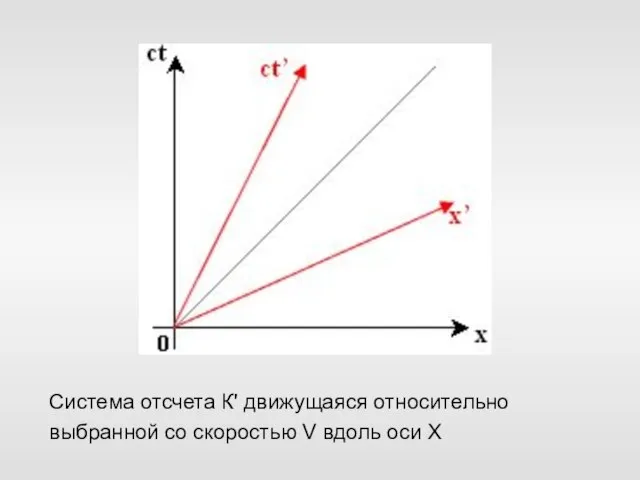
- 62. Графическое изображение разных систем отсчета в 4-мерном пространстве-времени Минковского
- 63. Система отсчета К' движущаяся относительно выбранной со скоростью V вдоль оси Х
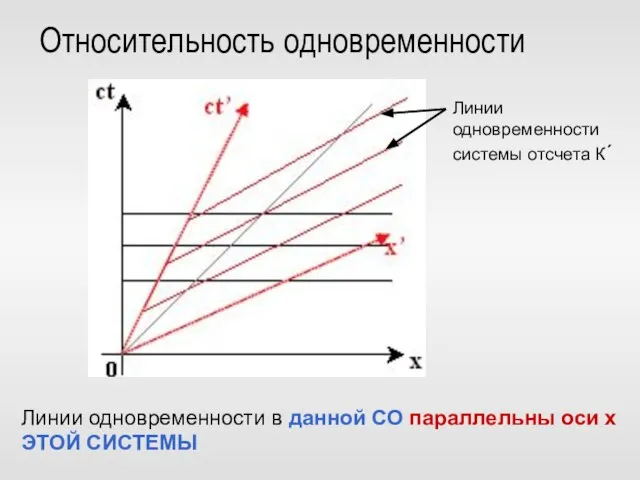
- 64. Относительность одновременности Линии одновременности в данной СО параллельны оси x ЭТОЙ СИСТЕМЫ
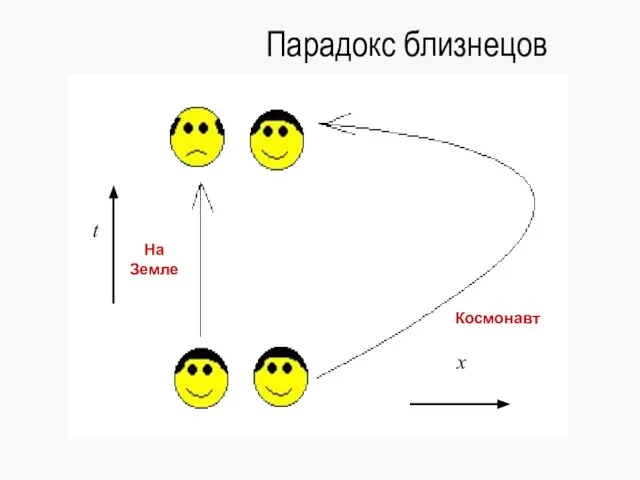
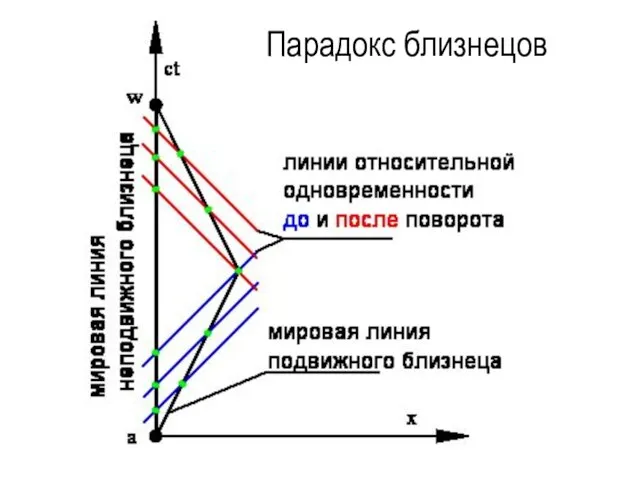
- 65. Парадокс близнецов
- 66. Парадокс близнецов
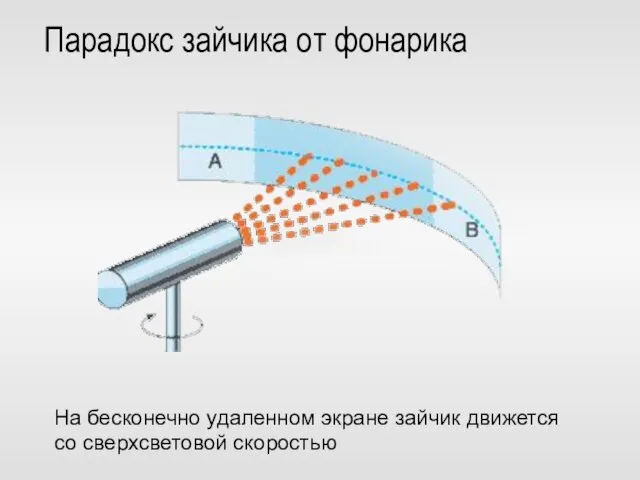
- 67. Парадокс зайчика от фонарика На бесконечно удаленном экране зайчик движется со сверхсветовой скоростью
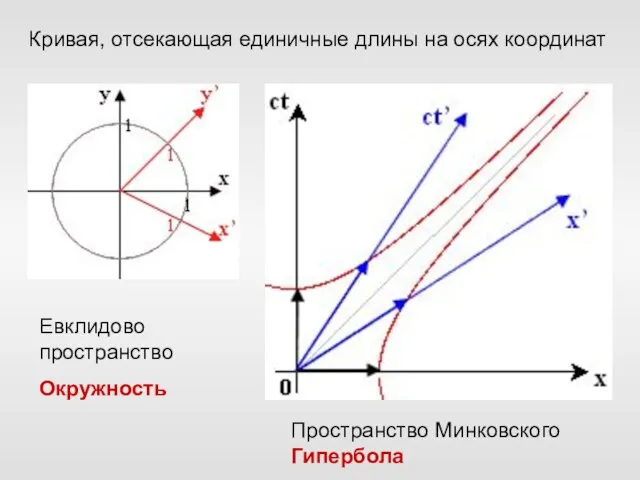
- 68. Кривая, отсекающая единичные длины на осях координат Евклидово пространство Окружность Пространство Минковского Гипербола
- 69. Источники Часть слайдов лекции взята (с изменениями) из презентаций курса Physics 2213b Modern Physics проф. Rick
- 71. Скачать презентацию











































 Колледж железнодорожной медицины
Колледж железнодорожной медицины Волож Аркадий Юрьевич Генеральный директор Соколов Алексей Юрьевич Директор по развитию сетевой инфраструктуры
Волож Аркадий Юрьевич Генеральный директор Соколов Алексей Юрьевич Директор по развитию сетевой инфраструктуры Небеса коснулись меня Я тону в присутствии Вижу на престоле Царя Он в меня поверил Чем могу воздать Тебе мой Бог
Небеса коснулись меня Я тону в присутствии Вижу на престоле Царя Он в меня поверил Чем могу воздать Тебе мой Бог «Личностно - ориентированное взаимодействие педагога и ребёнка на уроках коми языка и литературы»
«Личностно - ориентированное взаимодействие педагога и ребёнка на уроках коми языка и литературы» А.А.СапроновВице-президентОАО «НК «Роснефть»
А.А.СапроновВице-президентОАО «НК «Роснефть» Естественные системы человека для защиты от негативных воздействий
Естественные системы человека для защиты от негативных воздействий Мир Леонардо да Винчи15апреля1452г. – 2мая 1519г.
Мир Леонардо да Винчи15апреля1452г. – 2мая 1519г. Я люблю тебя, Татарстан
Я люблю тебя, Татарстан  Приготовление супов-пюре
Приготовление супов-пюре Торговый кодекс 1807 г. Развитие французского гражданского и торгового права в XIX – XX вв
Торговый кодекс 1807 г. Развитие французского гражданского и торгового права в XIX – XX вв Презентация на тему Приспособленность организмов к среде обитания
Презентация на тему Приспособленность организмов к среде обитания Подготовка кадров для рыночной электроэнергетикиК вопросу развития системы управления процессами государственного тарифного р
Подготовка кадров для рыночной электроэнергетикиК вопросу развития системы управления процессами государственного тарифного р Кафедра общей гигиены СамГМУ
Кафедра общей гигиены СамГМУ Презентация на тему Интерактивная доска
Презентация на тему Интерактивная доска Презентация на тему Жизнь и творчество Н.А. Заболоцкого
Презентация на тему Жизнь и творчество Н.А. Заболоцкого  К В Н по русскому языку
К В Н по русскому языку Дебюрократизация возвращение свободы
Дебюрократизация возвращение свободы Политические режимы
Политические режимы Острый и хронический ларингит. Отек и стеноз гортани
Острый и хронический ларингит. Отек и стеноз гортани  Дистанционные методы обучения
Дистанционные методы обучения 20141104_2_osobo_okhranyaemye_prirodnye_territorii_u._o
20141104_2_osobo_okhranyaemye_prirodnye_territorii_u._o Распределение солнечного тепла и света на Земле
Распределение солнечного тепла и света на Земле Решение показательных уравнений 10 класс
Решение показательных уравнений 10 класс Что такое сила трения, и что случится, если ее отменить?
Что такое сила трения, и что случится, если ее отменить? Создание документов в текстовых редакторах
Создание документов в текстовых редакторах Размножение на клеточном и организменном уровне
Размножение на клеточном и организменном уровне Панки
Панки Урок розвитку зв'язного мовлення.
Урок розвитку зв'язного мовлення.