ТЕПЛОЕМКОСТЬ ГАЗОВ. ЭНТРОПИЯ

ОТНОШЕНИЕ ТЕПЛОЕМКОСТЕЙ ср И сv
ОПРЕДЕЛЕНИЕ qv И qp ДЛЯ ИДЕАЛЬНЫХ ГАЗОВ ПО ТАБЛИЦАМ ТЕПЛОЕМКОСТЕЙ
ТЕПЛОЕМКОСТЬ СМЕСЕЙ ИДЕАЛЬНЫХ ГАЗОВ
ЭНТРОПИЯ. ВЫЧИСЛЕНИЕ ЭНТРОПИИ ИДЕАЛЬНОГО ГАЗА ДЛЯ ОБРАТИМЫХ И НЕОБРАТИМЫХ ПРОЦЕССОВ
ТЕПЛОВАЯ Ts - ДИАГРАММА

1. ОПРЕДЕЛЕНИЯ УДЕЛЬНОЙ (МАССОВОЙ), ОБЪЕМНОЙ И МОЛЯРНОЙ ТЕПЛОЕМКОСТИ ГАЗОВ
Сообщение телу теплоты в каком-либо процессе вызывает изменение его состояния и в общем случае сопровождается изменением температуры.
Отношение элементарного количества теплоты δq, полученного телом при бесконечно малом изменении его состояния, к изменению температуры dt называется удельной теплоемкостью тела в данном процессе:
(6.1)

Общее количество теплоты, полученное в данном процессе:
(6.2)
Поскольку количество теплоты зависит от характера процесса, то и теплоемкость системы сх также зависит от условий протекания процесса.
Одна и та же система в зависимости от характера процесса обладает различными теплоемкостями, численная величина которых может изменяться в пределах от — ∞ до + ∞.

Удельная (массовая) теплоемкость сх — величина, равная отношению теплоемкости однородного тела к его массе.
Единица удельной теплоемкости — джоуль на килограмм·Кельвин [Дж/(кг·К)], он равен удельной (массовой) теплоемкости вещества, имеющего при массе 1 кг теплоемкость 1 Дж/К.
Объемной теплоемкостью с'х называют отношение теплоемкости рабочего тела к его объему при нормальных физических условиях, т. е. при давлении 101 325 Па и температуре t = 0°С.
Единица объемной теплоемкости — джоуль на кубический метр · Кельвин [Дж/(м3·К)], он равен объемной теплоемкости рабочего тела, имеющего при объеме 1 м3 теплоемкость 1 Дж/К.

Молярной теплоемкостью сm называют величину, равную произведению удельной теплоемкости вещества на молярную массу этого вещества. Единицей молярной теплоемкости является джоуль на моль·Кельвин [Дж/(моль·К)], который равен молярной теплоемкости вещества, имеющего при количестве вещества 1 моль теплоемкость 1 Дж/К.
v0 — удельный объем при нормальных физических условиях; М — молярная масса

2. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ ТЕПЛОЕМКОСТЕЙ сv И сp
теплоемкость при постоянном объеме равная отношению количества теплоты δqv в процессе при постоянном объеме к изменению температуры dT тела:
(6.3)

теплоемкость при постоянном давлении равная отношению количества теплоты δqp в процессе при постоянном давлении к изменению температуры dТ тела:
(6.4)
При равновесном процессе нагревания тела элементарное количество теплоты определяем из уравнения (5.9):

Так как из уравнения (5.3):
(6.4’)
При v=const (dv=0):
(6.5)
- теплоемкость cv при v = const равна частной производной от внутренней энергии u (рассматриваемой как функция T и v) по температуре Т

Из уравнений (6.3) и (6.5) следует, что в процессе при v = const, в котором тело не совершает внешней работы, вся теплота, сообщаемая телу, идет на изменение его внутренней энергии:
(6.6)
Изменение внутренней энергии идеального газа равно произведению теплоемкости cv при постоянном объеме на разность температур тела в любом процессе

Для идеального газа, внутренняя энергия которого является функцией только температуры, частная производная:
Тогда, независимо от характера процесса:
или
Интегрируем уравнение (6.6) для идеального газа от 0 до t°C:
- средняя теплоемкость при v = const

Для любого конечного процесса изменения состояния идеального газа:
Подставляя значение в основное уравнение первого закона термодинамики (5.9), имеем в общем случае для обратимого процесса при бесконечно малом изменении состояния идеального газа:
(6.7)
Если в качестве независимых переменных принять Т и v, то из уравнения первого закона термодинамики получим:
(6.7’)

Отсюда при р = const :
или, поскольку
(6.8)
Применяя уравнение (6.5), получаем:
(6.9)
Уравнение (6.9) устанавливает в общем виде связь между теплоемкостями ср и cv

Для идеального газа, так как , а из
уравнения состояния
или
(6.10)
Для 1 моль:
Следовательно, для идеальных газов разность между сmр и cmv есть величина постоянная.
Дж/(моль·К)
Уравнение Майера:

Уравнение для теплоемкости ср можно получить, если в качестве независимых параметров взять давление р и температуру Т.
Согласно уравнению (5.13):
(6.11)
откуда следует, что р =const :
(6.12)
Теплоемкость тела ср при р = const равна частной производной от энтальпии h по температуре T и является функцией р и Т
или

Уравнение первого закона термодинамики:
Для идеального газа:
(6.13)
Первый закон термодинамики при независимых переменных v и Т представляется в виде:
Но
где
(6.14)
и

С помощью последнего уравнения можно найти зависимость между теплоемкостями ср и cv. Для изобарного процесса (при р = const) уравнение (6.14) принимает вид:
(6.15)
Разделим левую и правую части уравнения (6.15) на dTp:
принимая во внимание, что , получаем:
(6.16)
Если для реального газа известно уравнение состояния и ср, которая может быть определена из опыта, то формула (6.16) позволяет определить и cv, которую из опыта определить очень трудно.

Для реальных газов
Это неравенство объясняется тем, что при расширении реальных газов (при p = const) совершается не только внешняя, но и внутренняя работа, связанная с изменением внутренней потенциальной энергии тела, что и вызывает больший расход теплоты.

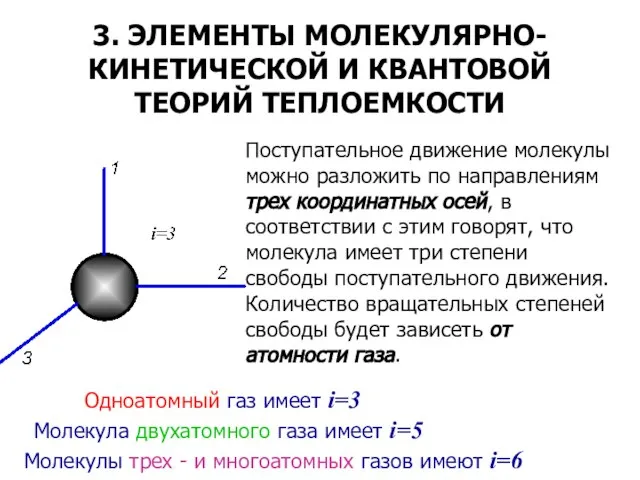
3. ЭЛЕМЕНТЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ И КВАНТОВОЙ ТЕОРИЙ ТЕПЛОЕМКОСТИ
Поступательное движение молекулы можно разложить по направлениям трех координатных осей, в соответствии с этим говорят, что молекула имеет три степени свободы поступательного движения. Количество вращательных степеней свободы будет зависеть от атомности газа.
Одноатомный газ имеет i=3
Молекула двухатомного газа имеет i=5
Молекулы трех - и многоатомных газов имеют i=6

Расчет доли внутренней энергии, приходящуюся на одну степень свободы одноатомного идеального газа:
(6.17)
Умножая обе части уравнения (6.17) на объем моля Vm, получим уравнение для 1 моль:
Произведение есть число атомов в 1 моль газа (число Авогадро):
где

Величина представляет собой среднюю кинетическую энергию поступательного движения одного атома газа, а так как общее число атомов равно N, то вся внутренняя энергия 1 моль одноатомного газа, равная кинетической энергии всех атомов, равна:
(6.18)
Заменяя pVm его значением из уравнения состояния, находим:
(6.19)

Так как Rm = 8,3142 Дж/(моль·К), то для одноатомного газа:
(6.20)
Взяв из уравнения (6.19) производную от внутренней энергии по температуре, имеем:
(6.21)
Из уравнения видно, что сmv не зависит от температуры. Следовательно, уравнение (6.19) выражает внутреннюю энергию одноатомного идеального газа, который подчиняется уравнению и у которого cmv=const.
Числовое значение мольной теплоемкости для одноатомного газа:
, Дж/(моль·К)

Отсюда на каждую степень свободы движения в одноатомном газе расходуется энергия — 12,5:3 = 4,16 Дж/(моль·К). Подставляя значение теплоемкости cmv из (6.21) в уравнение Майера, находим
(6.22)
или для одноатомного газа:
Для двухатомного газа:
, Дж/(моль·К)
, Дж/(моль·К)
, Дж/(моль·К)

Эйнштейн, пользуясь квантовой теорией Планка, получил следующее выражение для молярной теплоемкости, достаточно точное для температур, применяемых в теплотехнике:
(6.23)
где i1 — число степеней свободы поступательного и вращательного движений молекулы; i2 — число степеней свободы внутримолекулярных колебаний; θ — характеристическая температура колебательного движения, равная (h — постоянная Планка, k — постоянная Больцмана, ω — число колебаний в секунду); е — основание натуральных логарифмов; Т — абсолютная температура газа.

4. ИСТИННАЯ И СРЕДНЯЯ ТЕПЛОЕМКОСТИ
Теплоемкость, определяемая уравнениями (6.1), (6.3), (6.4) при данных значениях параметров состояния v и Т или р и Т (т. е. в данном состоянии тела), называют истинной теплоемкостью сх. Следовательно, истинной теплоемкостью называется отношение элементарного количества теплоты, сообщаемой термодинамической системе в каком-либо процессе, к бесконечно малой разности температур.

Первое слагаемое cx0 представляет собой теплоемкость данного газа в разреженном (идеально газовом) состоянии (при p→0 или v→∞) и зависит только от температуры.
Второе слагаемое Δсх определяет зависимость теплоемкости от давления или удельного объема и связано с изменением потенциальной составляющей внутренней энергии реального газа.

Средней теплоемкостью данного процесса в интервале температур от t1 до t2 называют отношение количества теплоты q1-2 к конечной разности температур t2 — t1:
(6.24)
Так как количество теплоты q1-2,x, полученное системой в процессе x = const, определяется уравнением (6.2), где сх — истинная теплоемкость в данном процессе, то
(6.25)

Если средние теплоемкости даны в таблице для интервала температур от 0 до t°С, то средняя теплоемкость может быть вычислена по формуле:
(6.26)
Величина средней теплоемкости есть высота прямоугольника 3456, площадь которого равновелика пл. 1234.

Таким образом, если в каком-либо процессе идеальный газ был нагрет от температуры t1 до t2, то количество теплоты, затраченное на нагревание, равно:
(6.27)

5. ОТНОШЕНИЕ ТЕПЛОЕМКОСТЕЙ ср И сv
Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме, обозначаемое обычно k:
Согласно классической кинетической теории газов, величина k определяется числом степеней свободы молекулы. Из уравнений (6.21) и (6.22) следует:
(6.28)

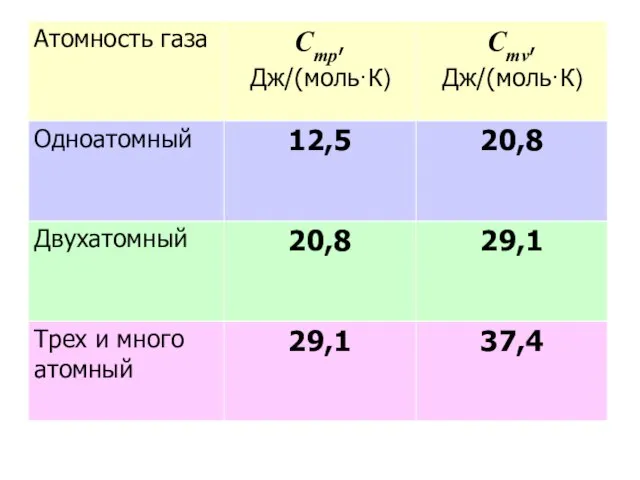
Если считать сx = const, то получаем:
для одноатомного газа k = 1,66;
для двухатомного газа k = 1,4;
для трех- и многоатомных газов k = 1,33.
При сх ≠ const для идеальных газов k зависит от температуры, что и видно из формулы:
(6.29)

6. ОПРЕДЕЛЕНИЕ qv И qp ДЛЯ ИДЕАЛЬНЫХ ГАЗОВ ПО ТАБЛИЦАМ ТЕПЛОЕМКОСТЕЙ
Следовательно, для определения теплоты qp и qv необходимо знать:
либо теплоемкости в интервале температур от 0 до t°C,
либо значения удельных энтальпий и внутренних энергий.
(6.30)
(6.31)

7. ТЕПЛОЕМКОСТЬ СМЕСЕЙ ИДЕАЛЬНЫХ ГАЗОВ
Если смесь газов задана массовыми долями, то удельная теплоемкость смеси определяется как сумма произведений массовых долей на удельную теплоемкость каждого газа:
(6.32)
(6.33)

Если смесь газов задана объемными долями, то объемная теплоемкость смеси равна сумме произведений объемных долей на объемную теплоемкость каждого газа:
(6.34)
(6.35)

Молярная теплоемкость смеси газов равна произведению объемных долей на молярные теплоемкости составляющих смесь газов:
Удельная теплоемкость смеси газов может быть определена, если известны плотность и удельный объем смеси газов при нормальных физических условиях:

8. ЭНТРОПИЯ. ВЫЧИСЛЕНИЕ ЭНТРОПИИ ИДЕАЛЬНОГО ГАЗА ДЛЯ ОБРАТИМЫХ И НЕОБРАТИМЫХ ПРОЦЕССОВ
(6.36)
Отсюда выражение δq/T при обратимом изменении состояния газа есть полный дифференциал некоторой функции переменных T и v (сv зависит только от температуры, а R — величина постоянная). Клаузиус назвал эту функцию энтропией и обозначил S. Выражается полная энтропия S в джоулях на градус (Дж/К), а удельная энтропия s - в джоулях на килограмм·градус [Дж/(кг·К)].

Дифференциал энтропии для обратимого изменения состояния определяется как
Удельная энтропия есть однозначная функция состояния газа, принимающая для каждого его состояния вполне определенное значение.
Является экстенсивным (зависит от массы вещества) параметром состояния, и изменение ее полностью определяется крайними состояниями тела и не зависит от пути процесса. В связи с этим энтропия газа, являясь параметром состояния, в процессах, 1-3-2, 1-4-2, 1-5-2, 1-6-2 (рис. 6.2) будет изменяться одинаково. Это свойство относятся как к обратимым, так и необратимым процессам.
(6.37)

Так как удельная энтропия обладает свойством аддитивности, то алгебраическая сумма изменений энтропии отдельных тел, составляющих термодинамическую систему, будет равна изменению энтропии всей термодинамической системы в целом. Причем изменения удельной энтропии отдельных тел в зависимости от процесса могут быть как положительными, так и отрицательными величинами.
Удельная энтропия может быть определена как функция основных параметров состояния:
Для получения изменения удельной энтропии как функции T и v соотношение (6.36) представим в следующем виде:
(6.38)

Интегрируя, при cv=const найдем для идеального газа:
(6.39)
Для получения изменения энтропии как функции Т и р следует из уравнения (6.38) исключить v. Из уравнения Клапейрона после дифференцирования получим:
Подставляя значение dv/v в уравнение (6.38), имеем:
Интегрируя, при cp=const находим:
(6.40)

Для получения изменения удельной энтропии как функции р и v следует из уравнения (6.38) исключить Т, Пользуясь тем же методом, получим:
(6.41)
Полученные уравнения (6.39), (6.40) и (6.41) применимы как для обратимых, так и для необратимых процессов.

Удельная теплоемкость сх любого процесса х равна произведению абсолютной температуры Т на частную производную удельной энтропии s по температуре Т при x = const:
(6.42)
Подставив в уравнения (5.9) и (5.13) значение δq из уравнения (6.37), получим:
(6.43)
(6.44)
Равенства (6.43) и (6.44) содержат только параметры состояния и их дифференциалы и носят название термодинамических тождеств; они относятся к обратимым процессам.

Если в термодинамической системе кроме работы изменения объема совершается работа δlv, не связанная с изменением объема тела, то термодинамические тождества имеют такой вид:
(6.45)
(6.46)
В термодинамике внутренняя энергия, энтальпия, энтропия, теплоемкости называются калорическими свойствами вещества, а удельный объем, абсолютное давление, температура — термическими свойствами.