Содержание
- 2. 5.1. ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ Первый закон термодинамики является частным случаем всеобщего закона сохранения и
- 3. К концу XVIII в. процесс превращения теплоты в работу был осуществлен, но без всяких теоретических расчетов
- 4. А — постоянная величина, называемая тепловым эквивалентом работы. Тепловой эквивалент единицы работы — величина размерная и
- 5. В 1843 г. англичанин Джоуль, а в 1844 г. русский академик Ленц установили соотношение между электрической
- 6. Таким образом, закон сохранения и превращения энергии, открытый М. В. Ломоносовым, но не получивший широкого развития
- 7. 5.2. ВНУТРЕННЯЯ ЭНЕРГИЯ Под внутренней энергией газа понимается вся энергия, заключенная в теле или системе тел:
- 8. Полную внутреннюю энергию тела принято обозначать U (Дж), а удельную внутреннюю энергию — u(Дж/кг) (5.2)
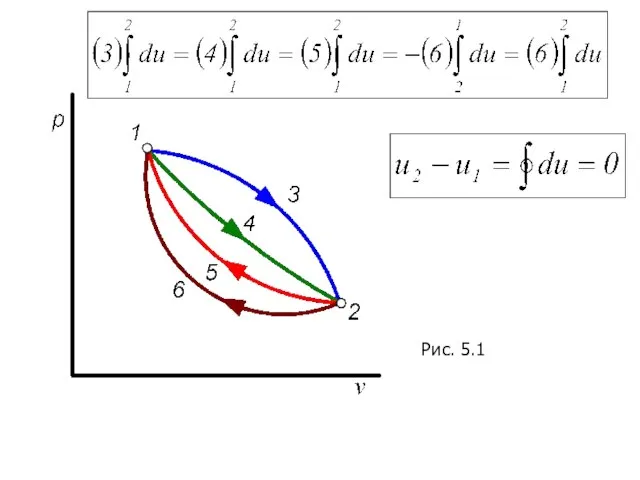
- 9. Рис. 5.1
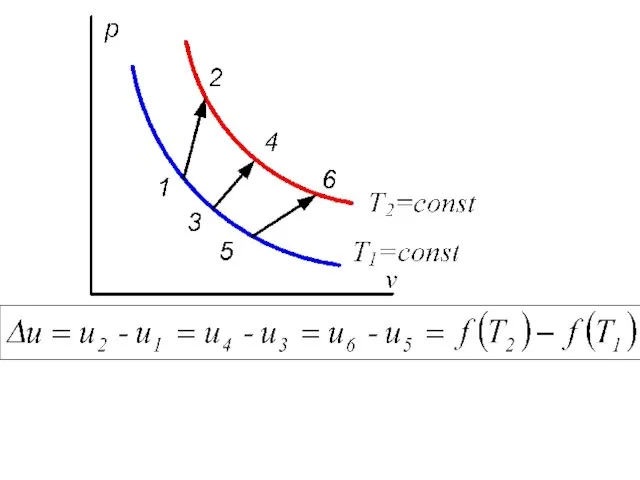
- 10. (5.3) Удельная внутренняя энергия идеального газа, в котором отсутствуют силы взаимодействия между молекулами, не зависит от
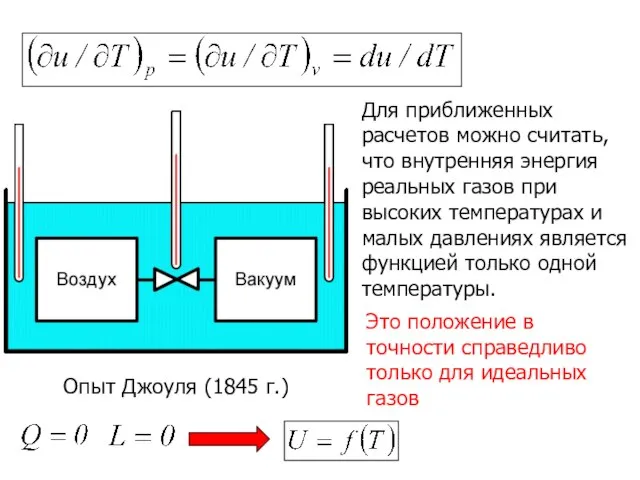
- 11. Для приближенных расчетов можно считать, что внутренняя энергия реальных газов при высоких температурах и малых давлениях
- 13. 5.3. АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ РАБОТЫ ПРОЦЕССА Передачу энергии от одного тела к другому, связанную с изменением объема
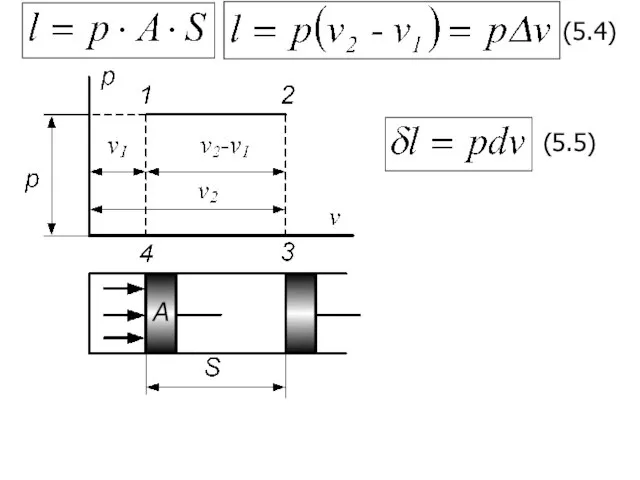
- 14. (5.4) (5.5)
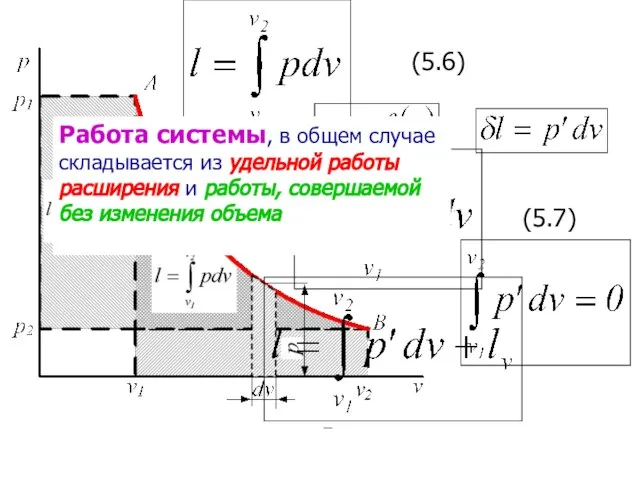
- 15. (5.6) (5.7) Работа системы, в общем случае складывается из удельной работы расширения и работы, совершаемой без
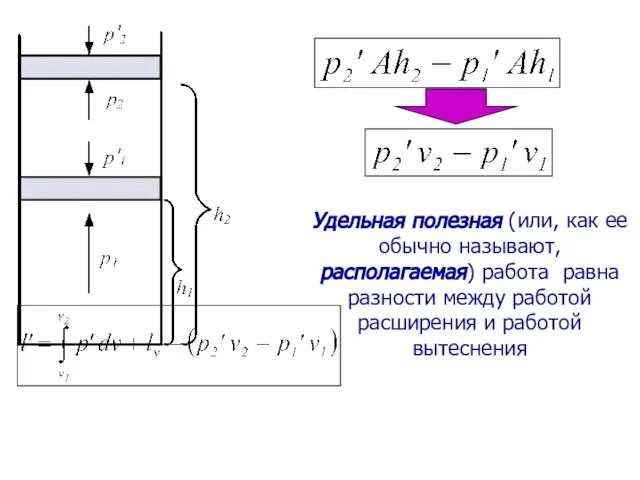
- 16. Удельная полезная (или, как ее обычно называют, располагаемая) работа равна разности между работой расширения и работой
- 17. Если v2 > v1 — газ расширяется, тогда Δv > 0 и dv > 0 —
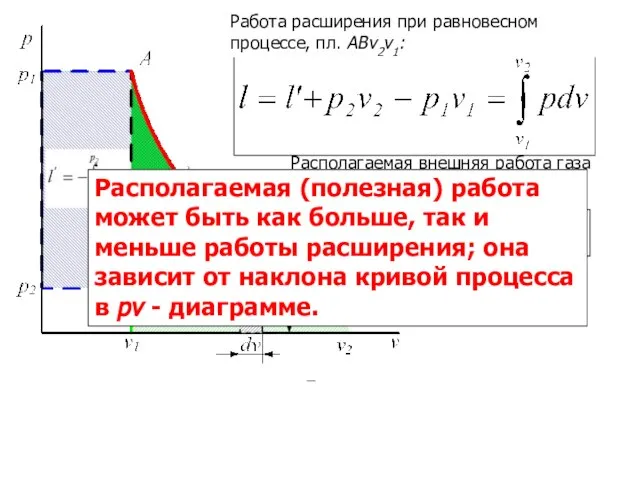
- 18. Работа расширения при равновесном процессе, пл. АВv2v1: Располагаемая внешняя работа газа (полезная), пл. АВр2p1: Располагаемая (полезная)
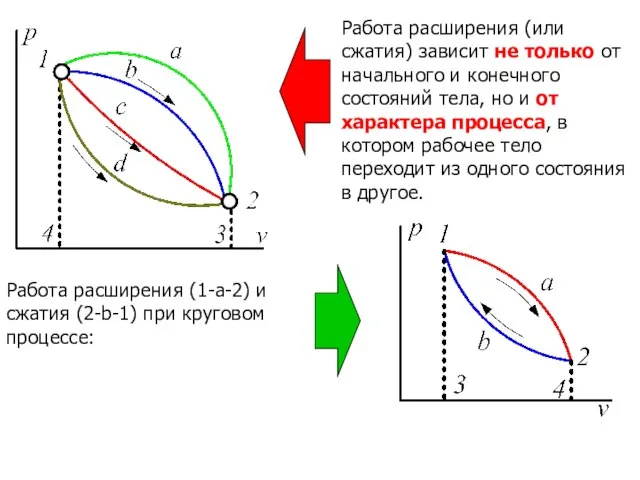
- 19. Работа расширения (или сжатия) зависит не только от начального и конечного состояний тела, но и от
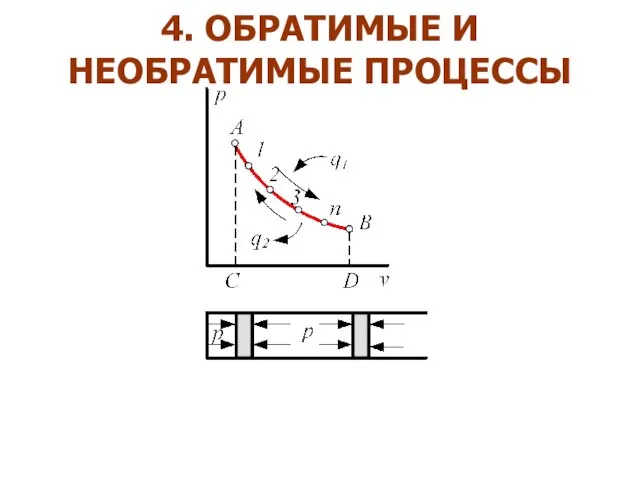
- 20. 4. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ
- 21. Процессы, протекающие в прямом и обратном направлениях без остаточных изменений, как в самом рабочем теле, так
- 22. Необратимыми термодинамическими процессами являются: процессы расширения и сжатия с конечными скоростями всякий процесс, сопровождающийся трением процессы,
- 23. При расширении газа всегда - При сжатии газа - Обратимый процесс представляет собой некоторый предельный случай
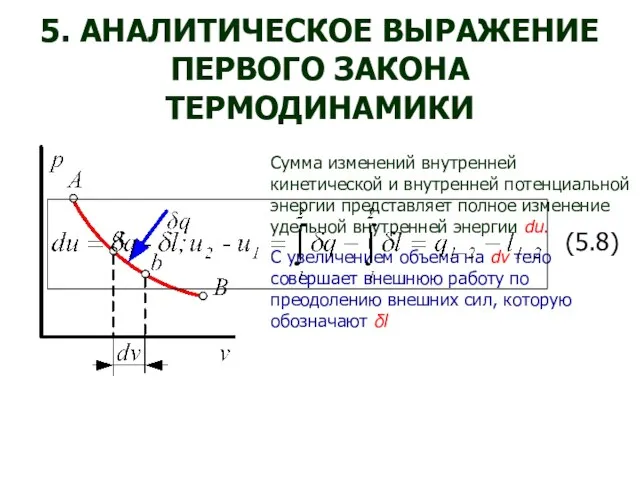
- 24. 5. АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ Сумма изменений внутренней кинетической и внутренней потенциальной энергии представляет полное
- 25. изменение удельной внутренней энергии термодинамической системы равно алгебраической сумме полученной системой энергии в форме удельной теплоты
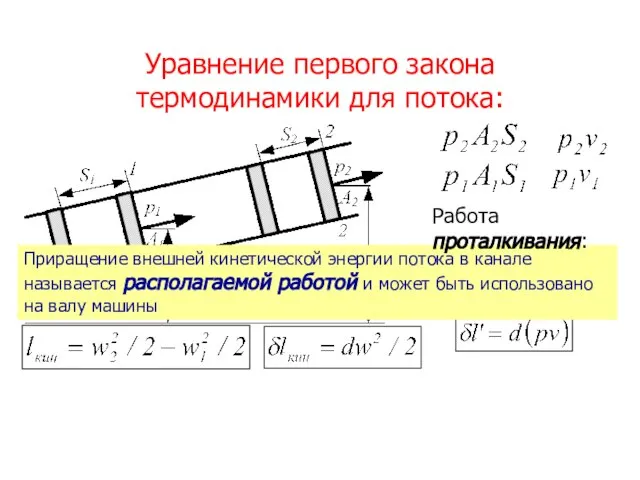
- 26. Уравнение первого закона термодинамики для потока: Приращение внешней кинетической энергии потока в канале называется располагаемой работой
- 27. Работа на изменение внешней потенциальной энергии потока в канале: В общем случае поток между сечениями канала
- 28. (5.10) Полученное уравнение первого закона термодинамики справедливо для любых рабочих тел и, в частности, для идеальных
- 29. (5.11) Уравнения (5.9) и (5.11) выражают первый закон термодинамики, а величину работы pdv можно приравнять правой
- 30. 6. ЭНТАЛЬПИЯ Удельная энтальпия, т.е. отношение энтальпии к массе тела, обозначается h и выражается в джоулях
- 31. (5.15) Удельная энтальпия системы определяется с точностью до некоторой аддитивной постоянной h0. Эту постоянную выбирают произвольно,
- 32. При p=const уравнение (5.13) превращается в (5.18) Дифференциал удельной энтальпии dh есть элементарное количество теплоты, участвующее
- 33. (5.21) Физический смысл энтальпии - удельная энтальпия h равна энергии расширенной системы — тела и окружающей
- 35. Скачать презентацию





















 Презентация на тему Очерк жизни и творчества
Презентация на тему Очерк жизни и творчества  TROS.2
TROS.2 Торговая Марка
Торговая Марка Урок 35. Придаточные предложения образа действия и степени.
Урок 35. Придаточные предложения образа действия и степени. В. Г. Распутин
В. Г. Распутин Сибирь, Алтайский край, Косихинский район. Именно здесь прошли детские и юношеские годы будущего космонавта 2 - Германа Степановича
Сибирь, Алтайский край, Косихинский район. Именно здесь прошли детские и юношеские годы будущего космонавта 2 - Германа Степановича Экономическое районирование России (9 класс)
Экономическое районирование России (9 класс) Чего ты хочешь…^3^
Чего ты хочешь…^3^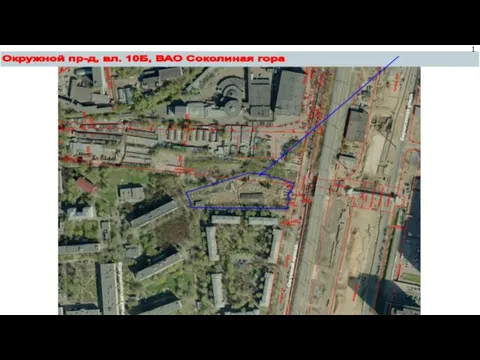 Окружной проезд, владение 10Б, ВАО Соколиная гора
Окружной проезд, владение 10Б, ВАО Соколиная гора Ярмарка домашней и фермерской продукции, авторских украшений, подарков и игрушек
Ярмарка домашней и фермерской продукции, авторских украшений, подарков и игрушек Задачи на расчет количества теплоты
Задачи на расчет количества теплоты Презентация на тему Производные предлоги
Презентация на тему Производные предлоги Дерматология: первичный прием.
Дерматология: первичный прием. Друзья Если плачет кто – то рядом, Если слезы льются градом, Подойдите вы к нему И спросите «Почему?» Это, дети, сделать надо – Плох
Друзья Если плачет кто – то рядом, Если слезы льются градом, Подойдите вы к нему И спросите «Почему?» Это, дети, сделать надо – Плох Батырлык дәресе “Кайнар йөрәк”
Батырлык дәресе “Кайнар йөрәк” Швейцарские банки
Швейцарские банки proektirovanie_bd_na_osnove_normalizatsii_teoria_polnaya
proektirovanie_bd_na_osnove_normalizatsii_teoria_polnaya Ребенок в школе
Ребенок в школе А.П Платонов «Никита»
А.П Платонов «Никита» Python 01_multi_new
Python 01_multi_new Экспериментальные модели артериальной гипертензии
Экспериментальные модели артериальной гипертензии В мастерской кондитера
В мастерской кондитера Конфликт
Конфликт Презентация на тему Африка растительный и животный мир
Презентация на тему Африка растительный и животный мир 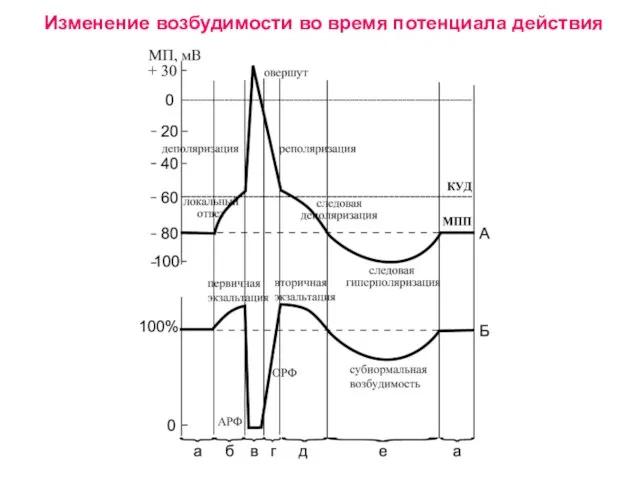 Изменение возбудимости во время потенциала действия
Изменение возбудимости во время потенциала действия Общение в Интернете
Общение в Интернете Внешнее строение листа
Внешнее строение листа Уважаемые родители!
Уважаемые родители!