Содержание
- 2. Мотивация Система знаний Психологическая готовность Результаты ЕГЭ
- 3. поиск разных способов решения этой задачи УРОК ОДНОЙ ЗАДАЧИ
- 4. Содержание задачи должно допускать вариативность решения. К уроку готовится общий для всех способов решения справочный материал.
- 5. 4. По окончании урока необходимо подвести итог, проанализировав какой из предложенных способов был наиболее рациональным, какой
- 6. Постановка проблемы. Мозговой штурм. Распределение на группы. Работа в группах. Представление решений. Рефлексия. Домашнее задание. Структура
- 7. Не все согласны, что важно научиться решать задачи несколькими способами, а как думаете вы? Отрытая проблема
- 8. 1.Геометрический способ (определение угла между плоскостями) 2.Аналитический способ (метод координат) 3.Геометрический способ (свойство ортогональной проекции) В
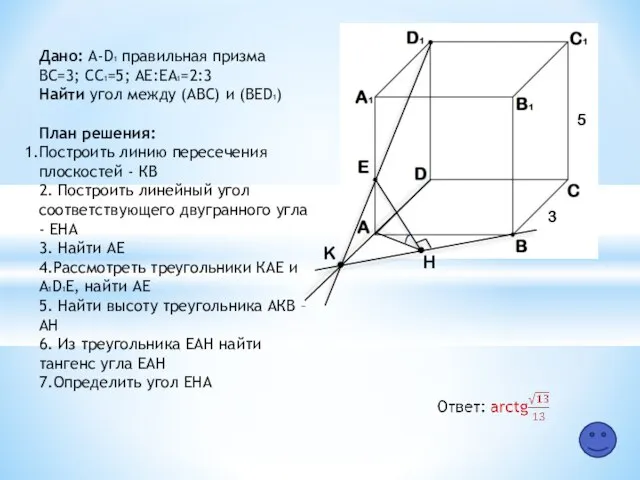
- 9. K H 5 3 Дано: A-D1 правильная призма ВС=3; СC1=5; АЕ:ЕA1=2:3 Найти угол между (АВС) и
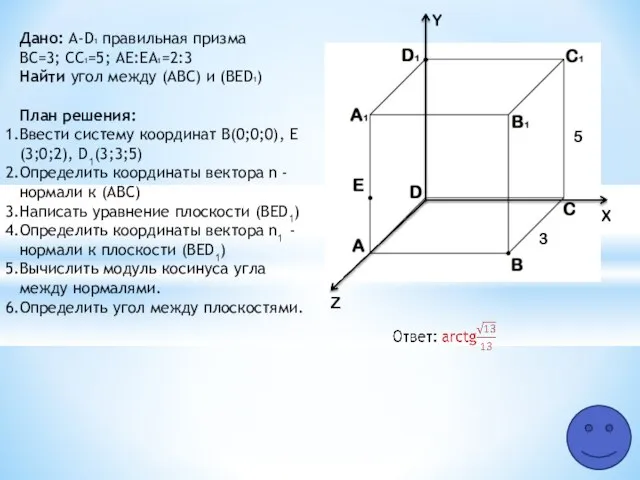
- 10. Z Y X 5 3 Дано: A-D1 правильная призма ВС=3; СC1=5; АЕ:ЕA1=2:3 Найти угол между (АВС)
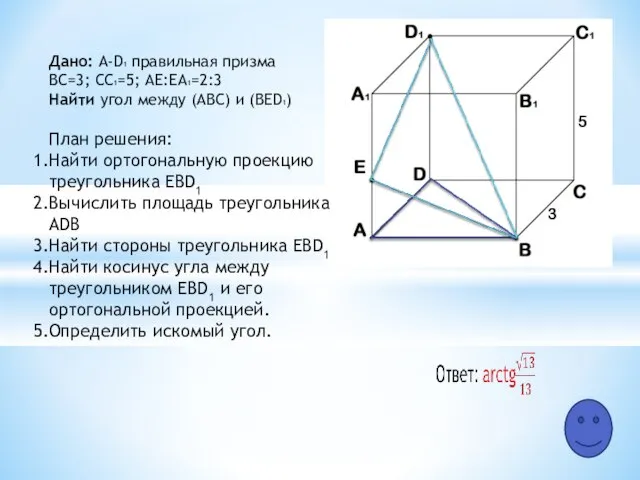
- 11. 5 3 Дано: A-D1 правильная призма ВС=3; СC1=5; АЕ:ЕA1=2:3 Найти угол между (АВС) и (ВЕD1) План
- 12. Отобрать необходимый теоретический материал (подсказка 1 уровня) Составить план решения задачи (подсказка 2 уровня) Оформить подробное
- 13. Какой из представленных путей решения вам показался наиболее рациональным, почему? Какой способ, по-вашему наиболее понятен? Какие
- 14. Обязательный уровень: Записать подробное решение задачи тремя способами Тренировочный уровень: Решить задачу несколькими способами: В правильной
- 16. Скачать презентацию










 Соленая рыба
Соленая рыба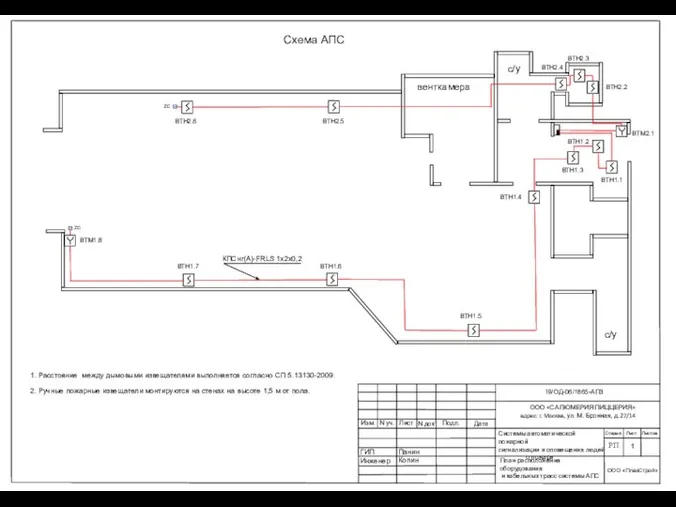 Схема АПС
Схема АПС Абсолютные и относительные статистические показатели
Абсолютные и относительные статистические показатели  Культура: понятие и сущность
Культура: понятие и сущность ИСПАРЕНИЕ ВЛАГИ ПОД ДЕЙСТВИЕМ СОЛНЦА
ИСПАРЕНИЕ ВЛАГИ ПОД ДЕЙСТВИЕМ СОЛНЦА МикротурбинаMTI 250
МикротурбинаMTI 250 Презентация на тему Двадцать четвёртое февраля
Презентация на тему Двадцать четвёртое февраля  Фотоальбом. От проекта до эксплуатации
Фотоальбом. От проекта до эксплуатации Запуск рекламы
Запуск рекламы Презентация команды АО МНИИТЭП
Презентация команды АО МНИИТЭП Особенности кожного покрова
Особенности кожного покрова презентация сайт
презентация сайт Новый человек в новых медиа
Новый человек в новых медиа Государственное управление в космической отрасли
Государственное управление в космической отрасли Презентация на тему Периметр и площадь прямоугольника
Презентация на тему Периметр и площадь прямоугольника  Играем и читаем
Играем и читаем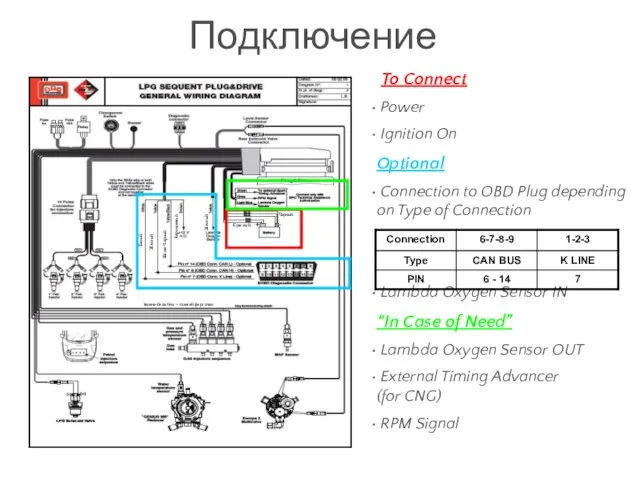 Подключение
Подключение Индивидуальное предпринимательство
Индивидуальное предпринимательство IP-система iPOLIS Samsung
IP-система iPOLIS Samsung Diagonal elements
Diagonal elements 1
1 Тиамин
Тиамин Основные фонды предприятия
Основные фонды предприятия Базовая сердечно-легочная реанимация
Базовая сердечно-легочная реанимация  Независимая оценка качества образования. Этапы формирования 1-х классов
Независимая оценка качества образования. Этапы формирования 1-х классов Использование параллелограмма в жизни
Использование параллелограмма в жизни координаты
координаты Регулирующая и надзорная деятельность банка России
Регулирующая и надзорная деятельность банка России