Содержание
- 2. Содержание: что такое функция история создания названия функции аналитический способ задания функции табличный способ задания функции
- 3. Что такое функция Две переменные величины Х и Y связаны функциональной зависимостью, если каждому значению, которое
- 4. Термин функция впервые появился в 1692 году у Лейбница и употреблялся в узком смысле (различные отрезки,
- 5. Аналитический способ задания функций Функция задается формулой, позволяющей получить значение зависимой переменной (Y),подставив конкретное числовое значение
- 6. Табличный способ задания функции При этом способе задания функции заполняется таблица, в верхней строке которой значения
- 7. Способ задания функции описанием Функцию можно задать описанием с помощью естественного языка. Например: «Каждому отрицательному числу
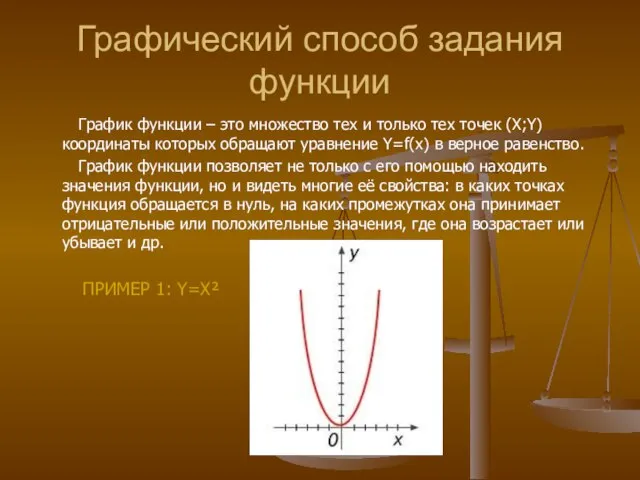
- 8. Графический способ задания функции График функции – это множество тех и только тех точек (X;Y) координаты
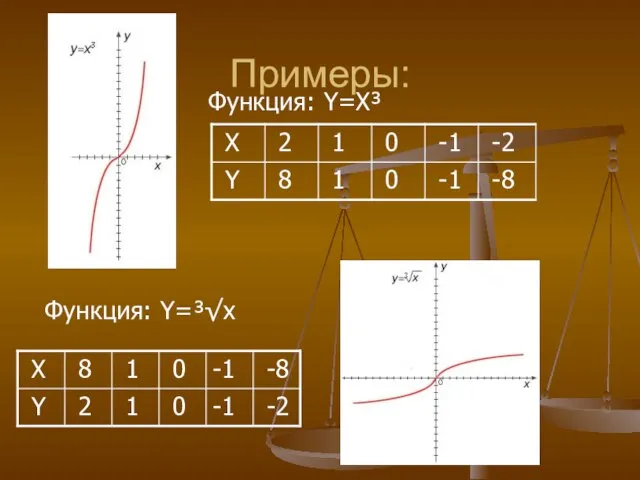
- 9. Примеры: Функция: Y=X³ Функция: Y=³√х
- 10. Область определения функции Область определения функции f(x) называется множество всех действительных значений независимой переменной х ,
- 11. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ Областью значений функции Y=f(x) называется множество всех действительных значений, которые принимает зависимая переменная
- 12. Примеры области определения и значения функции: Пример 1: Найдите область определения функции Y=2х/х-3. Решение: На нуль
- 13. Чётность, нечётность возрастание и убывание функции Функцию f называют чётной (соответственно нечётной), если её график симметричен
- 14. Примеры четности, нечетности, возрастания и убывания функции: Функция возрастает на промежутке (-∞;0) и убывает на промежутке
- 16. Скачать презентацию











 Искусство. Опрос. 4 класса
Искусство. Опрос. 4 класса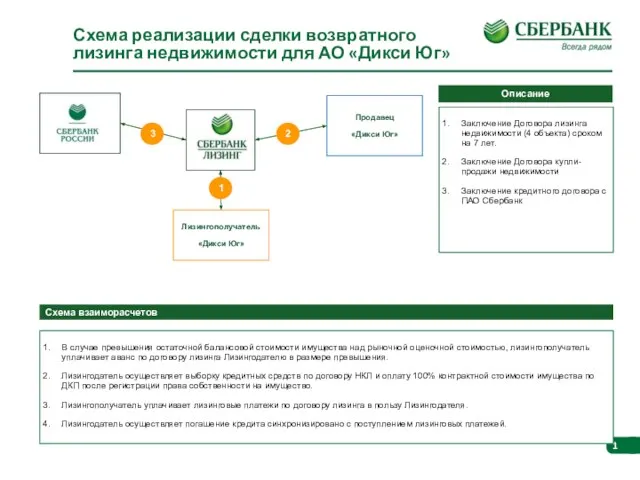 Схема реализации сделки возвратного лизинга недвижимости для АО Дикси Юг
Схема реализации сделки возвратного лизинга недвижимости для АО Дикси Юг Презентация на тему Оборона Сталинграда
Презентация на тему Оборона Сталинграда  Стиральные машины
Стиральные машины Эмоции и чувства. Занятие для первоклассников
Эмоции и чувства. Занятие для первоклассников Давление. Сила давления
Давление. Сила давления Зимние виды спорта
Зимние виды спорта Kursovoy_proekt_Kuzovkin_M_A_EE-19-3b (1)
Kursovoy_proekt_Kuzovkin_M_A_EE-19-3b (1) Практический экзамен по физической культуре в 9 классе
Практический экзамен по физической культуре в 9 классе Демонология романа "Мастер и Маргарита"
Демонология романа "Мастер и Маргарита" Киселевский художник - Селищев Михаил Григорьевич
Киселевский художник - Селищев Михаил Григорьевич Презентация на тему Профессия Экономист
Презентация на тему Профессия Экономист История Олимпийских игр
История Олимпийских игр Индустрия питания. Предприятия общественного питания
Индустрия питания. Предприятия общественного питания Уральское таможенное управление_
Уральское таможенное управление_ Сказкотерапия как инновационная технология духовно-нравственного воспитания средствами авторской сказки
Сказкотерапия как инновационная технология духовно-нравственного воспитания средствами авторской сказки Настурция
Настурция Бешбармак по-казахски
Бешбармак по-казахски Презентация на тему Сахалин
Презентация на тему Сахалин  Плавание и его воздействие на развитие системы опорно-двигательного аппарата
Плавание и его воздействие на развитие системы опорно-двигательного аппарата Образование. Приоритетность (преобладающее значение) образования
Образование. Приоритетность (преобладающее значение) образования Презентация на тему Объединение земель
Презентация на тему Объединение земель Явление радиоактивности
Явление радиоактивности Как дружить без ссоры
Как дружить без ссоры Выразительность произведений великих художников Ивана Айвазовского и Ореста Адамовича Кипрейского
Выразительность произведений великих художников Ивана Айвазовского и Ореста Адамовича Кипрейского ПРЕЗЕНТАЦИЯ 7 «б» классаНАШИ ДОСТИЖЕНИЯ
ПРЕЗЕНТАЦИЯ 7 «б» классаНАШИ ДОСТИЖЕНИЯ «Использование компьютерных презентаций на уроках иностранного языка»
«Использование компьютерных презентаций на уроках иностранного языка» Идеальная бровь
Идеальная бровь