Слайд 2Устойчивость дискретных систем
Необходимость. Предположим сначала, что условие
(13.1) не выполняется, то есть

.
Рассмотрим ограниченную последовательность, заданную значениями:
Так как выходные отсчеты сигнала равны свертке входных отсчетов и значений импульсной характеристики дискретной системы, то есть
то при отклик системы равен:
Слайд 3Устойчивость дискретных систем
Достаточность. Предположим, что условие (13.1) выполняется, а на вход поступает

ограниченная последовательность отсчетов сигнала . Из формулы свертки входного сигнала и импульсной характеристики получаем:
Если , то
и система – устойчива.
Слайд 4Устойчивость дискретных систем
Устойчивость нерекурсивных дискретных систем. Как ранее отмечалось, в нерекурсивных дискретных

системах для вычисления очередного отсчета выходного сигнала используются только отсчеты входного сигнала
. Поэтому алгоритм работы такой системы имеет вид:
Системная (передаточная) функция такой системы является рациональной функцией, то есть полиномом степени комплексного аргумента :
Слайд 5Устойчивость дискретных систем
Нерекурсивные стационарные линейные фильтры обладают замечательной особенностью: их импульсные характеристики

имеют конечное число ненулевых отсчетов, причем эти отсчеты равны коэффициентам алгоритма фильтрации.
Действительно
Отсюда следует, что
Таким образом, импульсная характеристика нерекурсивного стационарного линейного фильтра имеет конечное число отличных от нуля отсчетов, и в соответствии с (13.1) такой фильтр всегда устойчив.
Слайд 6Устойчивость дискретных систем
Устойчивость рекурсивных дискретных систем. Для рекурсивных дискретных систем использовать критерий

устойчивости в форме (13.1) затруднительно, поскольку необходимо суммировать бесконечный ряд модулей отсчетов импульсной характеристики. Выразим критерий (13.1) в другой форме, удобной для исследования рекурсивных фильтров.
Рассмотрим физически реализуемый фильтр порядка с системной функцией и для простоты предположим, что все полюсы простые. Отметим, что для физически реализуемых фильтров степень полинома в числителе не превышает степень полинома в знаменателе.
Слайд 7Устойчивость дискретных систем
Импульсная характеристика такого фильтра определяется соотношением:
Для имеем:
а при имеем следующее

выражение:
Слайд 8Устойчивость дискретных систем
Представляя полюсы в виде: , полагая при
этом что ,

можно записать следующее соотношение:
Из анализа этого соотношения следует:
Так как по условию , то ряд в правой части соотношения сходится и
Слайд 9Устойчивость дискретных систем
Итак, если полюса функции лежат внутри круга единичного радиуса Z-плоскости,

то такой фильтр устойчив. Если хотя бы один полюс расположен на единичной окружности или во внешней части круга единичного радиуса, то такая представляет неустойчивый фильтр. Заметим, что положение нулей системной функции не влияет на устойчивость фильтра.
Недостатки полюсного критерия устойчивости обусловлены необходимостью определения корней характеристического уравнения, являющихся полюсами системной функции. Аналитических методов решения алгебраических уравнений, порядок которых выше четвертого, не существует. Поэтому нахождение полюсов высокого порядка возможно лишь численными методами.
Слайд 10Устойчивость дискретных систем
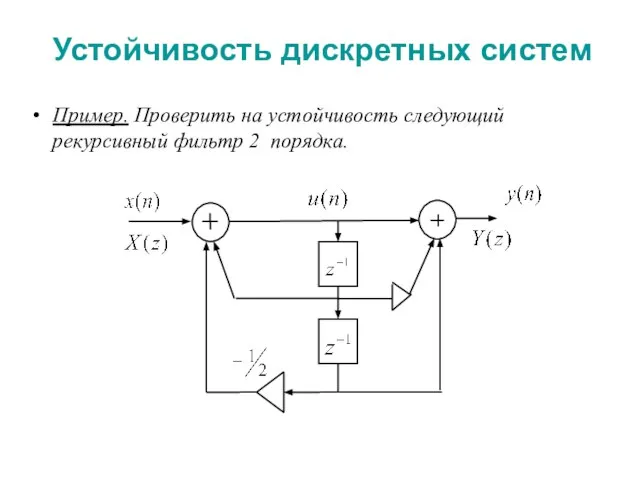
Пример. Проверить на устойчивость следующий рекурсивный фильтр 2 порядка.









 Отдельные виды договорных отношений в жилищном праве
Отдельные виды договорных отношений в жилищном праве Организация велостоянки для гимназии №1
Организация велостоянки для гимназии №1 О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го
О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го Урок русского языка в 6 классе по теме: «Правописание сложных существительных»
Урок русского языка в 6 классе по теме: «Правописание сложных существительных» Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании
Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании Невидимые нити в весеннем лесу (2 класс)
Невидимые нити в весеннем лесу (2 класс) Игрушки из носочков своими руками №7
Игрушки из носочков своими руками №7 Введение в специальность
Введение в специальность Герцог Ами
Герцог Ами Трение. Вредно или полезно
Трение. Вредно или полезно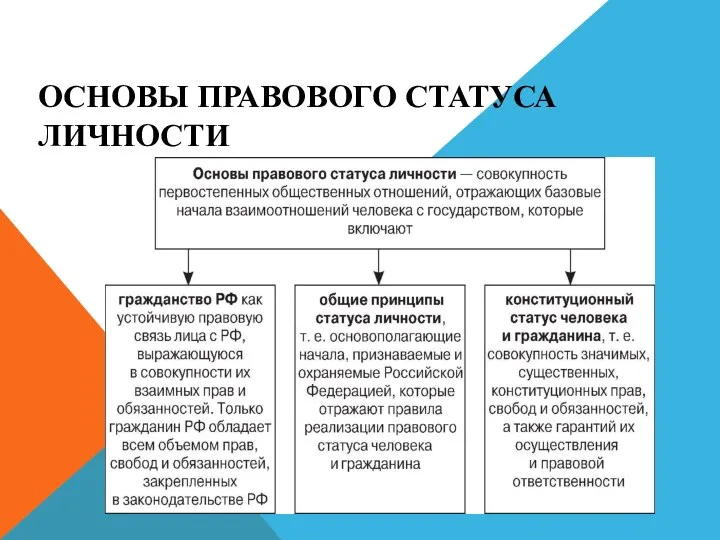 Правовой статус личности. Гражданство РФ
Правовой статус личности. Гражданство РФ Социальная психология
Социальная психология Презентация на тему АФАНАСИЙ НИКИТИН
Презентация на тему АФАНАСИЙ НИКИТИН  Теория обучения
Теория обучения Презентация на тему Our Environment (Наша окружающая среда)
Презентация на тему Our Environment (Наша окружающая среда) Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС)
Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС) Презентация по информатике на тему: «Устройства вывода информации, монитор.»
Презентация по информатике на тему: «Устройства вывода информации, монитор.» Круглопольское сельское поселение
Круглопольское сельское поселение Прайс косметологических услуг салона Забота о вас
Прайс косметологических услуг салона Забота о вас Патрон грязеуловителя
Патрон грязеуловителя Назначение изделия и его описание
Назначение изделия и его описание Планирование и организация процесса закупок материальных ресурсов промышленного предприятия
Планирование и организация процесса закупок материальных ресурсов промышленного предприятия Распространение объектно-ориентированного подхода на информационную безопасность
Распространение объектно-ориентированного подхода на информационную безопасность Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк.
Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк. Пейзаж в графике
Пейзаж в графике Рогожка. Коллекция однотонных штор
Рогожка. Коллекция однотонных штор _Презентация. Предоставление
_Презентация. Предоставление Презентация
Презентация