Содержание
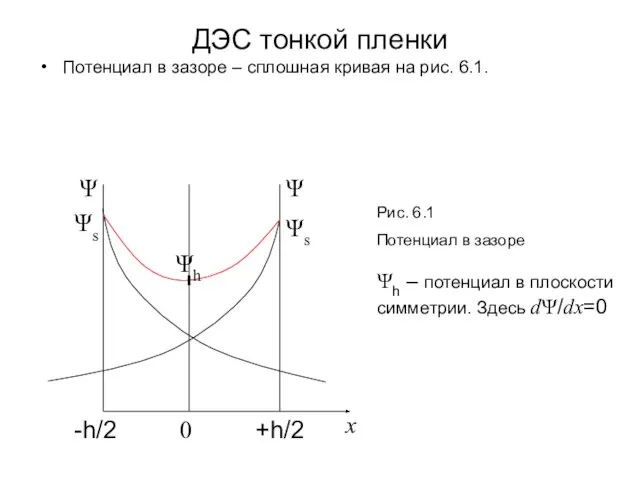
- 2. ДЭС тонкой пленки Потенциал в зазоре – сплошная кривая на рис. 6.1. Ψh – потенциал в
- 3. U(h) = 2[σ(h) - σ(∞)] (6.1) σ(∞) = - (1/2)qsΨs , где qs=εε0æΨs, Ψ= A1 exp(-æx)
- 4. Ψs = Ψhch(æh/2) , то Ψh = Ψs/ch(æh/2), Ψ = Ψsch(æx) / ch(æh/2) (6.3) qs= -
- 5. Производная: dΨ/dx = æΨssh(æx) / ch(æh/2) При x= - h/2 (dΨ/dx)s = - æΨssh(æh/2) / ch(æh/2),
- 6. Молекулярное притяжение Принцип аддитивности молекулярных взаимодействий: Потенциальная энергия U1 взаимодействия двух молекул U1= - A1/r6 (6.7)
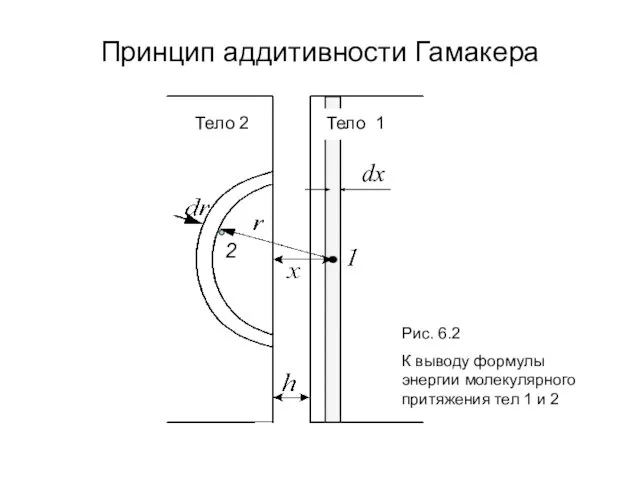
- 7. Принцип аддитивности Гамакера Тело 2 Рис. 6.2 К выводу формулы энергии молекулярного притяжения тел 1 и
- 8. dUм=Ua (NA/Vm)dx. интегрирование выражения (π/6)(NA/Vm)2A1dx / x3 в пределах от x=h до x= ∞ дает Uм=
- 10. Скачать презентацию
![U(h) = 2[σ(h) - σ(∞)] (6.1) σ(∞) = - (1/2)qsΨs , где](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/462609/slide-2.jpg)
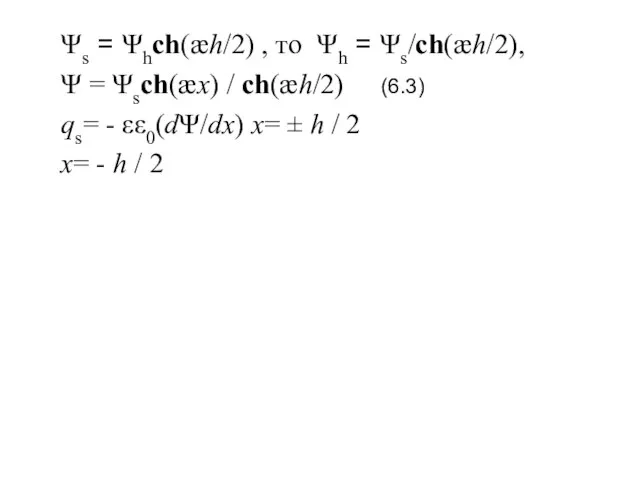



 Индекс массы тела. Показатель пропорциональности физического развития
Индекс массы тела. Показатель пропорциональности физического развития История, предмет, методология и структура современной психологии
История, предмет, методология и структура современной психологии Дадыкина Петр 1
Дадыкина Петр 1 Колодки и диски UBS
Колодки и диски UBS Гипер и супер маркеты
Гипер и супер маркеты Маркетинг общий
Маркетинг общий Аппарат «Астер»
Аппарат «Астер» Антивирусы TrustPort
Антивирусы TrustPort Арматура
Арматура Наводнения (7 класс)
Наводнения (7 класс) Интернет - урок
Интернет - урок Уникальность Продукции с торговой маркой
Уникальность Продукции с торговой маркой Совершенствование таможенного администрирования
Совершенствование таможенного администрирования Психология делового общения
Психология делового общения Агрохолдинг Московский. Тоиаты. Опыт выращивания
Агрохолдинг Московский. Тоиаты. Опыт выращивания Профориентация в русле ФГОС нового поколения
Профориентация в русле ФГОС нового поколения СТРАТЕГИЯ РАЗВИТИЯ ГОСУДАРСТВЕННОЙ НАЛОГОВОЙ СЛУЖБЫ ПРИ ПРАВИТЕЛЬСТВЕ КР на 2012-2014 гг.
СТРАТЕГИЯ РАЗВИТИЯ ГОСУДАРСТВЕННОЙ НАЛОГОВОЙ СЛУЖБЫ ПРИ ПРАВИТЕЛЬСТВЕ КР на 2012-2014 гг. Обучение (1) (1) (1)
Обучение (1) (1) (1) Цена, рынок, конкуренция
Цена, рынок, конкуренция Энергетические и освежающие напитки, лимонады, столовая вода
Энергетические и освежающие напитки, лимонады, столовая вода Всероссийский творческий фестиваль Верим в село! Гордимся Россией!
Всероссийский творческий фестиваль Верим в село! Гордимся Россией! Пейзаж и его роль в романе М.Ю.Лермонтова «Герой нашего времени»
Пейзаж и его роль в романе М.Ю.Лермонтова «Герой нашего времени» Фасад здания
Фасад здания Народный костюм
Народный костюм Связь ономастики с профессией судоводителя
Связь ономастики с профессией судоводителя Batel. Сетевой маркетинг
Batel. Сетевой маркетинг Обязанности судей перед игрой
Обязанности судей перед игрой Вторичное использование газет и журналов
Вторичное использование газет и журналов