Векторы на плоскости

СОДЕРЖАНИЕ
Векторные величины
Вектор
Построение вектора
Абсолютная величина. Равные векторы
Нулевой вектор
Коллинеарные векторы
Сонаправленные векторы, противоположно направленные векторы
Свойство коллинеарных векторов

Векторные величины
Величины, которые характеризуются не только числом, но и еще и направлением, называются векторными величинами или просто векторами.
Скорость
Ускорение
Сила

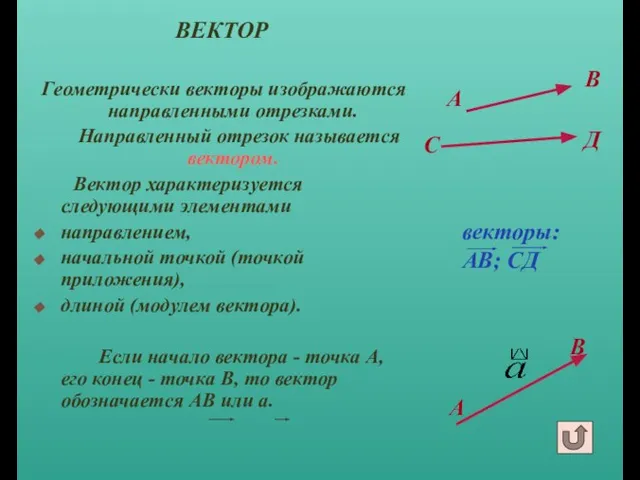
А
ВЕКТОР
Геометрически векторы изображаются направленными отрезками.
Направленный отрезок называется вектором.
Вектор характеризуется следующими элементами
направлением,
начальной точкой (точкой приложения),
длиной (модулем вектора).
Если начало вектора - точка А, его конец - точка В, то вектор обозначается АВ или а.
С
Д
В
векторы:
АВ; СД
А
В

От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
MN =
.
.
.

Абсолютная величина. Равные векторы.
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.
Абсолютная величина вектора а обозначается | а | .
Два вектора называются равными, если они совмещаются параллельным переносом.
АВСD – параллелограмм, АВ=DС

Нулевой вектор.
Нулевой вектор - точка в пространстве.
Начало и конец нулевого вектора совпадают, и он не имеет направления.
Длина нулевого вектора равна нулю.
Обозначается |О|.

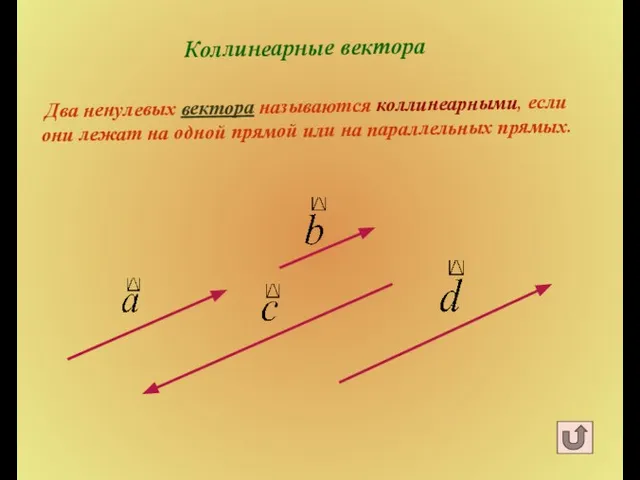
Коллинеарные вектора
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Сонаправленные и противоположно направленные вектора
Если векторы а и в коллинеарны и их лучи сонаправлены, то векторы а и в называются сонаправленными.
Обозначаются а в.
Если векторы а и d коллинеарны, а их лучи не являются сонаправленными, то векторы а и d называются противоположно направленными.
Обозначаются а d.
Нулевой вектор условились считать сонаправленным с любым вектором.