Содержание
- 2. Различие силы тяжести и веса На любое тело, находящееся на поверхности Земли (кроме полюса) действует центробежная
- 3. Момент инерции МТ относительно оси вращения Величина угловой скорости При вращении по окружности момент импульса МТ
- 4. Уравнение моментов для материальной точки Как уже говорилось момент импульса МТ, двигающейся по окружности: Производная по
- 5. Абсолютно твердое тело Под твердым телом будем подразумевать абсолютно твердое тело, в котором расстояния между любыми
- 6. Момент инерции твердого тела Твердое тело можно представить как систему МТ, удерживаемых внутренними силами на неизменных
- 7. Уравнением моментов Заменив в выражении для кинетической энергии массу на момент инерции I, а скорость v
- 8. Фигуристка на льду и Торнадо: Что общего? Сохранение кинетической энергии? Приблизительно ! Торнадо – увеличивается масса
- 9. Условия равновесия твердого тела В общем случае для равновесия абсолютно твердого тела необходимо выполнение двух условий.
- 10. Момент инерции в природе Самолеты убирают шасси во время полета, а, например, пчелы, напротив, вытягивают вперед
- 11. Механика поступательного и вращательно движения относительно неподвижной оси Все выражения для МТ и для твердого тела
- 12. Момент инерции полого цилиндра Найдем момент инерции полого цилиндра относительно его оси симметрии ОО. где m
- 13. Момент инерции сложных тел Для полного определения момента инерции более сложных тел выражение следует уточнить, устремив
- 14. Момент инерции сплошного цилиндра и однородного шара Момент инерции сплошного однородного цилиндра относительно оси симметрии ОО
- 15. Теорема Штейнера Зная момент инерции тела относительно оси, проходящей через центр масс, момент инерции относительно произвольной
- 17. Скачать презентацию














 Характеристика стран восточной Европы
Характеристика стран восточной Европы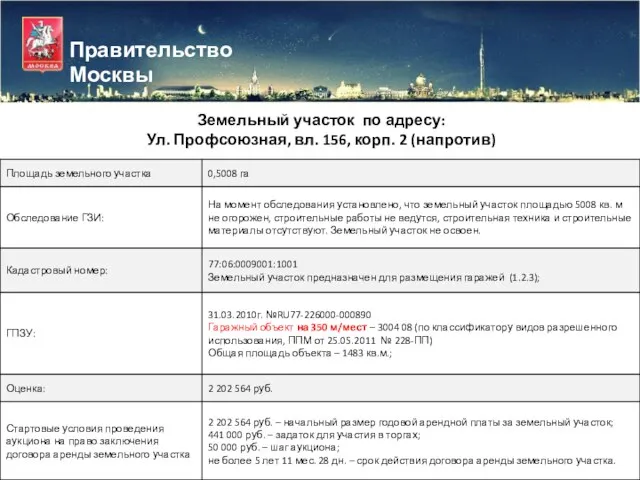 Правительство Москвы
Правительство Москвы Психолого – педагогическая служба в образовательном процессе
Психолого – педагогическая служба в образовательном процессе Стандарты кредитной надежности
Стандарты кредитной надежности Методика оценки командной эффективности. Социальные драйверы командной эффективности
Методика оценки командной эффективности. Социальные драйверы командной эффективности T-fest
T-fest Студенты-гуманитарии и вытеснение “систематического” мышления “поисковым”:к постановке проблемы
Студенты-гуманитарии и вытеснение “систематического” мышления “поисковым”:к постановке проблемы Презентация на тему Страны Африки. Ливия
Презентация на тему Страны Африки. Ливия  Проведение недель профессионального мастерства как форма коллективной методической работы
Проведение недель профессионального мастерства как форма коллективной методической работы  OpenOffice.org Writer
OpenOffice.org Writer GK120产品保养调整介绍
GK120产品保养调整介绍 Таргетированная реклама
Таргетированная реклама Musical Crossword
Musical Crossword Работа с контурной картой возраст гор
Работа с контурной картой возраст гор Учимся рисовать гуашью букет подсолнухов
Учимся рисовать гуашью букет подсолнухов ВИДЫ ТЕПЛОПЕРЕДАЧИ
ВИДЫ ТЕПЛОПЕРЕДАЧИ 23 февраля День защитника Отечества
23 февраля День защитника Отечества Растения Красной книги
Растения Красной книги Интегрированный урок в начальной школе
Интегрированный урок в начальной школе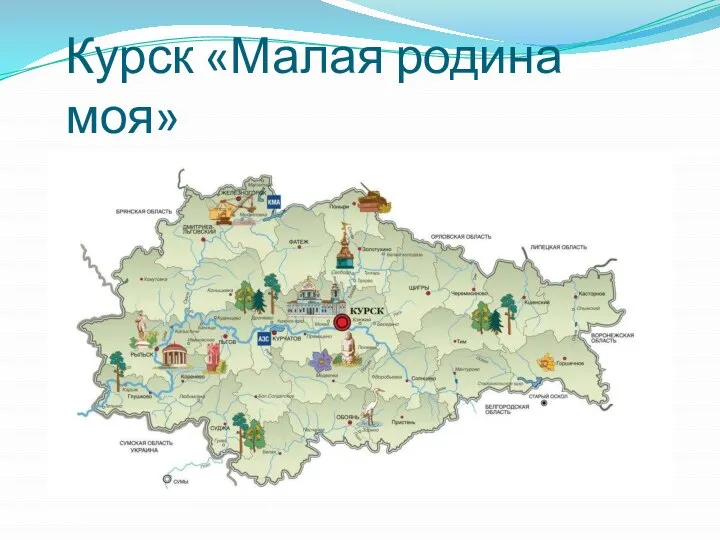 Курск Малая родина моя
Курск Малая родина моя Organic therapy
Organic therapy Приходи в Диснейленд
Приходи в Диснейленд אנחנו רוצים מחברות חדשות
אנחנו רוצים מחברות חדשות Христианская семья
Христианская семья Изготовление ящика для инструментов
Изготовление ящика для инструментов Воспитательный потенциал семьи
Воспитательный потенциал семьи Приходи на ФПММ — у нас интересно!
Приходи на ФПММ — у нас интересно! Биография Ф. И. Тютчева
Биография Ф. И. Тютчева