условия…
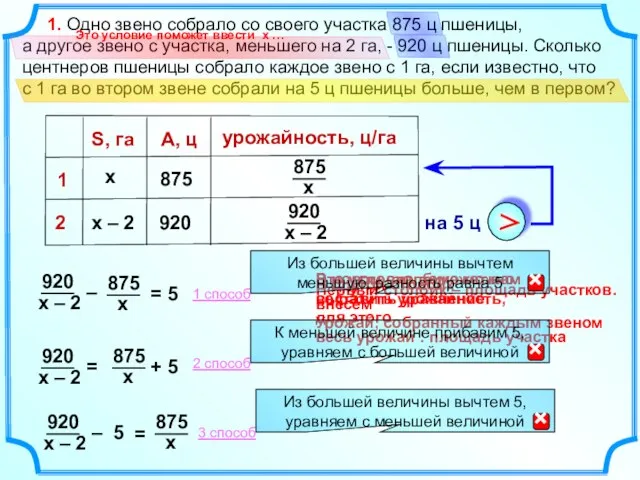
Одно звено собрало со своего участка 875 ц пшеницы,
а другое звено с участка, меньшего на 2 га, - 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что
с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом?
Это условие помогло ввести х …
А можно начать «раскручивать» задачу с другого условия. Введем х иначе…
Одно звено собрало со своего участка 875 ц пшеницы,
а другое звено с участка, меньшего на 2 га, - 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что
с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом?
Это условие поможет ввести х …
Посмотрим, что получится? В этом случае мы «выйдем» сразу на ответ, ведь за х будет обозначена искомая величина.








 Техники эффективного обучения
Техники эффективного обучения История успеха HYAMATRIX
История успеха HYAMATRIX Эпоха возрождения
Эпоха возрождения Реклама - двигатель торговли
Реклама - двигатель торговли ВОЙНОВА АНАСТАСИЯ группа МЭ082
ВОЙНОВА АНАСТАСИЯ группа МЭ082 Виртуальная экскурсия «Школьный мемориальный музей «памяти О.Е.Филипповой»»
Виртуальная экскурсия «Школьный мемориальный музей «памяти О.Е.Филипповой»» Баскетбол
Баскетбол 3f1245a5185fb3888a173f44c6e85193
3f1245a5185fb3888a173f44c6e85193 Семья – глаза в глаза
Семья – глаза в глаза Шестнадцатеричная_система_счисления
Шестнадцатеричная_система_счисления Базовой курс информатики
Базовой курс информатики Презентация на тему Сложение скоростей
Презентация на тему Сложение скоростей Запорожье
Запорожье Архитектура ЭВМ. Логические основы ЭВМ
Архитектура ЭВМ. Логические основы ЭВМ Урок-практикум.Обобщение изученного материала. Подготовка к ЕГЭ.«Это непростое простое повторение?!...» 11 класс.
Урок-практикум.Обобщение изученного материала. Подготовка к ЕГЭ.«Это непростое простое повторение?!...» 11 класс. МОСКВА 2012
МОСКВА 2012 Итоги проведения областной олимпиады и конкурса профессионального мастерства 2021г
Итоги проведения областной олимпиады и конкурса профессионального мастерства 2021г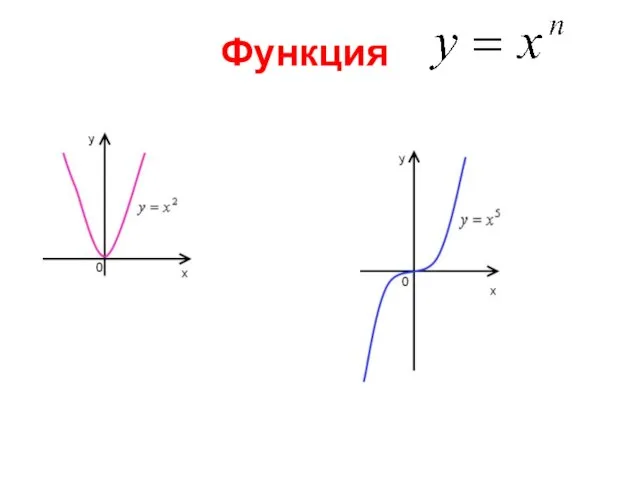 Функция
Функция Презентация на тему Загрязнение вод
Презентация на тему Загрязнение вод  3 причины освоить скорочтение
3 причины освоить скорочтение Презентация на тему Общение как понимание урок 10 класс
Презентация на тему Общение как понимание урок 10 класс Сім_я
Сім_я "Б У С Ы"
"Б У С Ы" Влияние курения на центральную нервную систему в подростковом периоде. Выполнила: Пименова Анастасия,
Влияние курения на центральную нервную систему в подростковом периоде. Выполнила: Пименова Анастасия,  Оценка временной стоимости денег в общественном секторе экономики
Оценка временной стоимости денег в общественном секторе экономики Жирные кислоты
Жирные кислоты Найти обстоятельства
Найти обстоятельства Пасхальные традиции в России
Пасхальные традиции в России