The game “Towers of Hanoi”

Recursion
procedure Solve(n: integer; a,b,c: Char);
begin
if n > 0 then
begin
Solve(n-1, a, c, b);
Writeln(‘transfer', a, ‘to rod',b);
Solve(n-1, c, b, a);
end;
end;
begin
Solve(4, '1','2','3');
end.

Mathematical induction method
14 + 24 + … + n4 = ?

Mathematical induction in geometry
1. Several straight lines were drawn on the plane. Prove that it is possible to color the plane in two colors so that the two areas that have a common part of the border have a different color. Areas that have only one common vertex may be of the same color.
2. Prove that a square can be cut into any number of squares, starting with 6.
3. Prove that for every N > 2 exists N–gon with three acute angles.
4. Prove that the square 2N х 2N, from which one cell was cut can be cut into “corners” of three cells.

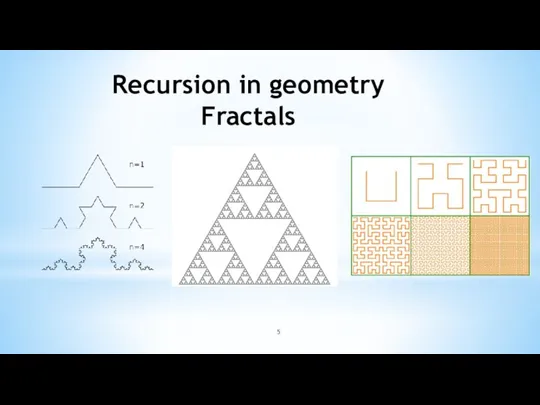
Recursion in geometry
Fractals

1. In the company of 2n + 1 people for any n people there is a different person from them who is familiar with each of them. Prove that in this company there is a person who knows everyone.
From n to (n +1)
2. Among the participants of the conference, everyone has at least one friend. Prove that the participants can be distributed in two rooms so that each participant has a friend in the other room.
We can reduce the problem for example with a tree

Calculation of the determinants + verifiation

Calculation of the determinants + verifiation
Solve the equation

Optimization

Inverse matrix
Solve the equation

Interpolation and verification
Lagrange interpolation polynomial