Задачи небесной механики

Задачи небесной механики (4h).
Закон всемирного тяготения.
Законы Кеплера. Орбиты планет и комет.
Понятие о задаче трёх тел.
Устойчивость планетной системы.
Поверхность и предел Роша.

Закон всемирного тяготения

Законы Кеплера.
Орбиты планет и комет

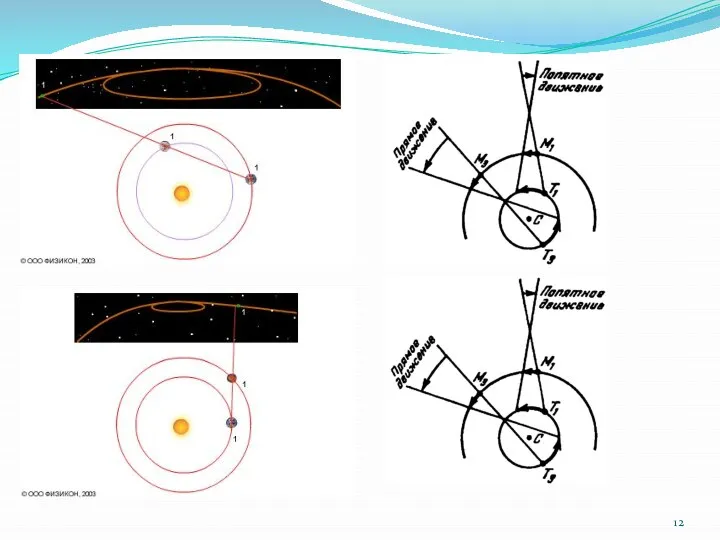
Видимое движение планет
Прямое движение – с запада на восток
Обратное движение – с востока на запад

Конфигурация нижних планет
У нижних планет и других небесных тел, чьи орбиты расположены внутри земной орбиты, различают:
соединения с Солнцем при которых планета и Солнце имеют одинаковую эклиптическую долготу (или одинаковое прямое восхождение)
верхнее соединение (Солнце находится между планетой и Землей)
нижнее соединение (планета находится между Солнцем и Землей)
наибольшие элонгации, соответствующие наибольшему видимому угловому расстоянию планеты от Солнца:
наибольшую восточную элонгацию
наибольшую западную элонгацию.
Вблизи верхнего соединения нижние планеты недоступны для наблюдения, так как находятся за Солнцем, скрываясь в его лучах. Непосредственно перед нижним соединением и после него нижние планеты видны в виде узкого серпа. Во время нижнего соединения возможно прохождение Меркурия или Венеры по диску Солнца, однако из-за относительного наклона планетарных орбит фактическое прохождение происходит достаточно редко, обычно при нижнем соединении нижняя планета находится выше или ниже Солнца по эклиптической широте. В элонгациях нижние планеты имеют вид светлого полудиска.

Конфигурация верхних планет и Луны
У Луны, верхних планет, а также других тел Солнечной системы, чья орбита лежит полностью вне земной орбиты, различают:
соединения с Солнцем, при которых планета и Солнце имеют одинаковую эклиптическую долготу (или одинаковое прямое восхождение);
противостояния, при которых эклиптические долготы (прямое восхождение) планеты и Солнца отличаются на 180°;
восточные и
западные квадратуры.
Вблизи соединений верхние планеты находятся за Солнцем и не видны.

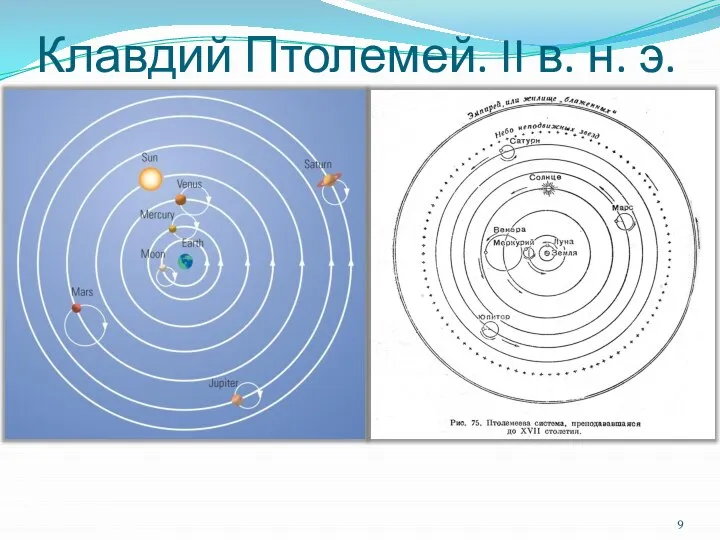
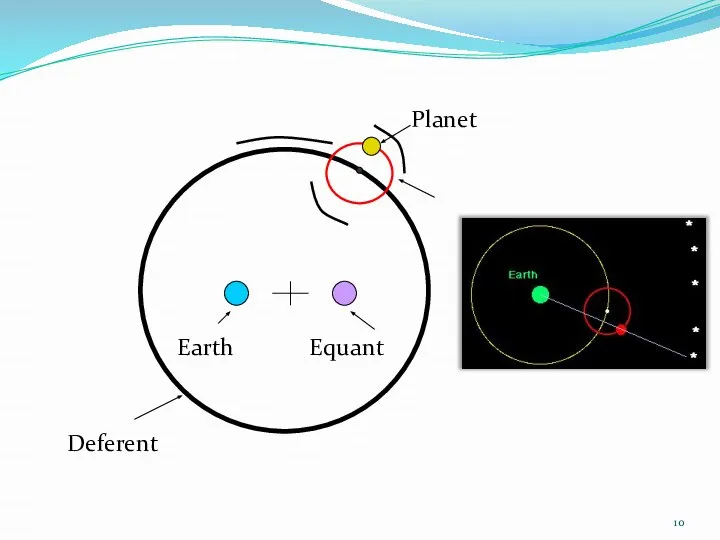
Клавдий Птолемей. II в. н. э.

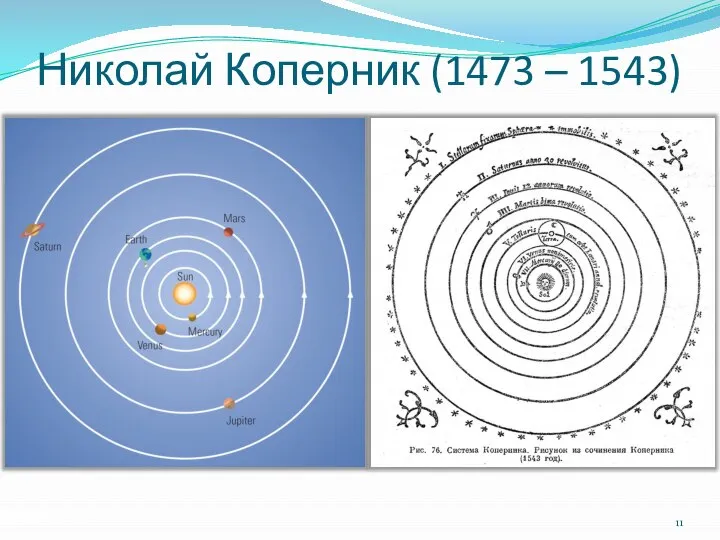
Николай Коперник (1473 – 1543)

Синодический и сидерический периоды обращения планет

Законы Кеплера
Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.
Радиус-вектор планеты в равные промежутки времени описывает равновеликие площади.
Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.
Законы получены как обобщение данных наблюдений

I закон Кеплера
a – большая полуось;
b – малая полуось;
с – фокальный радиус (полурасстояние между фокусами);
p – фокальный параметр;
rp – перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
ra – апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);
Первый закон Кеплера. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.
Современная формулировка первого закона: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола.

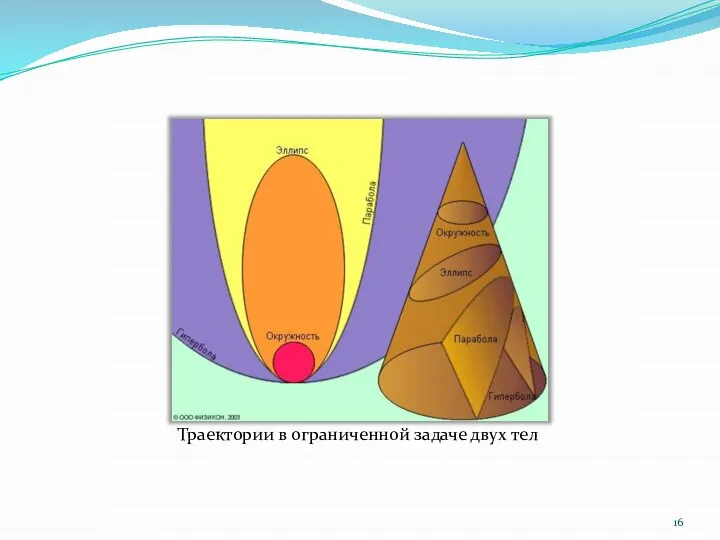
Траектории в ограниченной задаче двух тел

II закон Кеплера
Второй закон Кеплера (закон равных площадей). Радиус-вектор планеты за равные промежутки времени описывает равновеликие площади. Другая формулировка этого закона: секториальная скорость планеты постоянна.

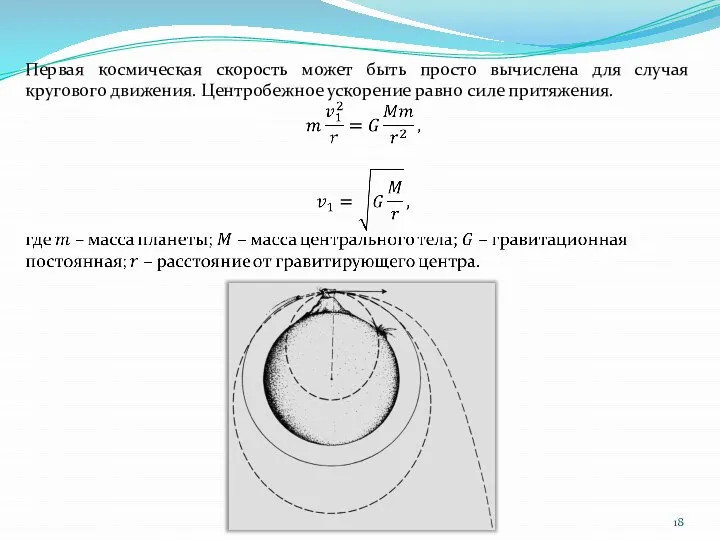
Первая космическая скорость может быть просто вычислена для случая кругового движения. Центробежное ускорение равно силе притяжения.

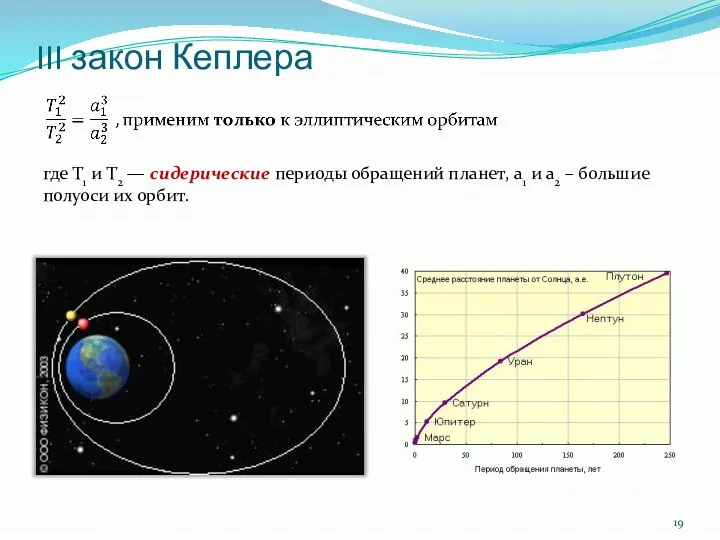
III закон Кеплера
где Т1 и T2 — сидерические периоды обращений планет, a1 и a2 – большие полуоси их орбит.

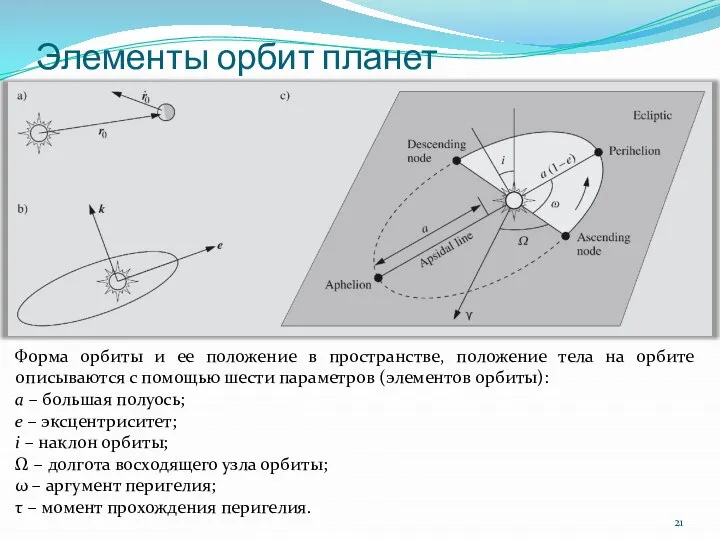
Элементы орбит планет
Форма орбиты и ее положение в пространстве, положение тела на орбите описываются с помощью шести параметров (элементов орбиты):
a – большая полуось;
e – эксцентриситет;
i – наклон орбиты;
Ω – долгота восходящего узла орбиты;
ω – аргумент перигелия;
τ – момент прохождения перигелия.

Положение тела на орбите

Определив эксцентрическую аномалию можно вычислить истинную аномалию и, тем самым, полностью описать движение тела по реальной орбите.

Понятие о задаче трех тел

Частные решения ограниченной задачи трех тел
Лагранж показал, что если третье тело находится в одной из этих пяти точек и обладает определенным значением начальной скорости, то конфигурация, которую образуют все три тела, всегда остается подобной самой себе, а движение всех тел происходит по коническим сечениям одинакового вида.
Три тела расположены на одной прямой и обращаются, оставаясь на ней, вокруг общего центра масс. Конфигурация неустойчива по отношению к малым возмущениям.
Три тела расположены в вершинах равностороннего треугольника и обращаются вокруг общего центра масс так, что треугольник остается все время равносторонним.

Устойчивость планетной системы.
Возмущенное движение
Невозмущенное движение = задача двух тел.
В задаче n тел орбиты перестают быть истинно кеплеровыми = возмущенное движение.
Зависимость элементов орбиты тела от времени вследствие притяжения его другими телами, помимо центрального, называется возмущениями или неравенствами элементов.
Возмущения описываются суммой линейной и множества периодических функций с различными значениями периодов. Линейные члены называются вековыми возмущениями, а остальные слагаемые – периодическими возмущениями.
Коэффициенты в функциях, представляющих возмущения, как правило, весьма малы, однако за достаточно большой промежуток времени вековые возмущения могут стать сколь угодно большими.
Наибольший интерес представляют вековые возмущения больших полуосей, эксцентриситетов и углов наклона орбит планет, поскольку именно они определяют характер устойчивости Солнечной системы.
Как следует из теории движения планет, вековые возмущения элементов орбит а, е и i чрезвычайно малы, и есть основания полагать, что Солнечная система устойчива по крайней мере в течение весьма длительных промежутков времени, возможно достигающих даже нескольких миллиардов лет.
Из остальных элементов орбиты – долгота восходящего узла Ω, и аргумент перигелия ω – подвержены значительным вековым возмущениям, которые в силу малости эксцентриситетов и наклонений орбит планет практически не изменяют общую конфигурацию Солнечной системы.

Дальнейшее уточнение теории движения планет приводит к появлению квадратичных и кубических по времени возмущений элементов орбит. Согласно теории, вполне возможно, что сумма таких возмущений может представлять собой начальные члены разложения в степенной ряд некоторой периодической функции. В этом случае изменение всех элементов будет ограниченным.
Вопрос об устойчивости Солнечной системы на неограниченном интервале времени пока остается открытым.

Ускорения w' и w" составляют ускорение возмущающей силы и обусловливают отклонения в движении планеты Р1 от законов Кеплера. Возмущающая сила, следовательно, состоит из двух сил: из силы действия планеты Р2 на планету Р1 и из силы действия планеты Р2 на Солнце. Так как ускорение w" откладывается в сторону, противоположную w2, то ускорение от возмущения есть разность векторов ускорений, вызываемых возмущающим телом на планете и на Солнце.
Возмущающая сила (возмущающее ускорение) в общем случае не направлена к возмущающему телу, т. е. к планете Р2. Возмущающая сила будет направлена точно к возмущающему телу Р2 только в том случае, если тела P1 и Р2 находятся на одной прямой с Солнцем, и притом оба по одну сторону от него (в порядке СР1Р2 или СР2Р1). Если же тела Р1 и Р2 находятся на одной прямой с Солнцем, но по разные стороны от него (Р1СР2), то возмущающая сила направлена от возмущающего тела. Величина и направление возмущающей силы вследствие движения тел непрерывно меняются.

Поверхность и предел Роша