Законы Кеплера

Иоганн Кеплер (1571-1630). Выдающийся немецкий астроном и математик, открывший законы движения планет вокруг Солнца. Кеплер был активным сторонником учения Коперника и своими работами способствовал его утверждению и развитию.

Заслуга открытия законов движения планет принадлежит выдающемуся немецкому ученому Иоганну Кеплеру (1571-1630).Заслуга открытия законов движения планет принадлежит выдающемуся немецкому ученому Иоганну (1571-1630). Кеплеру (1571-1630). В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.

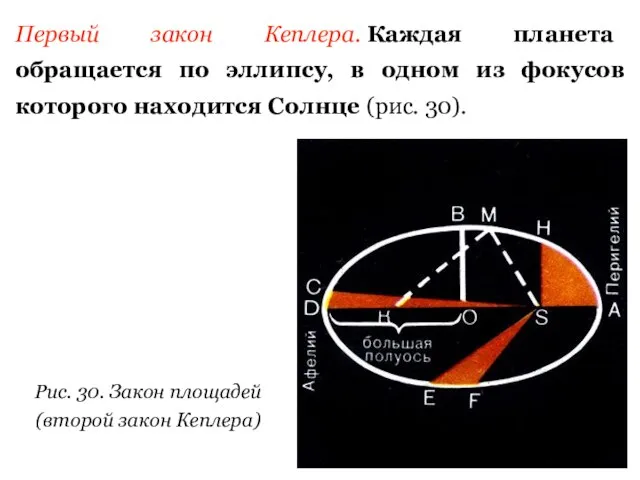
Первый закон Кеплера. Каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце (рис. 30).
Рис. 30. Закон площадей (второй закон Кеплера)

Эллипсом (см. рис. 30) называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний каждой ее точки от двух точек, называемых фокусами, остается постоянной. Эта сумма расстояний равна длине большой оси DA эллипса. Точка О - центр эллипса, К и S - фокусы. Солнце находится в данном случае в фокусе S. DO=OA=a - большая полуось эллипса. Большая полуось является средним расстоянием планеты от Солнца:

Ближайшая к Солнцу точка орбиты А называется перигелием, а самая далекая от него точка D - афелием.
Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет равен отношению расстояния фокуса от центра (OK=OS) к длине большой полуоси а, т. е.
При совпадении фокусов с центром (е=0) эллипс превращается в окружность.

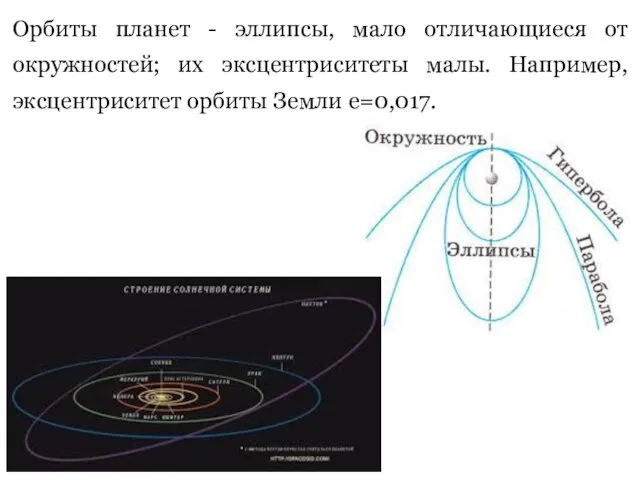
Орбиты планет - эллипсы, мало отличающиеся от окружностей; их эксцентриситеты малы. Например, эксцентриситет орбиты Земли е=0,017.

Второй закон Кеплера (закон площадей). Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади, т. е. площади SAH и SCD равны (см. рис. 30), если дуги
иописаны планетой за одинаковые промежутки времени. Но длины этих дуг, ограничивающих равные площади, различны:>. Следовательно, линейная скорость движения планеты неодинакова в разных точках ее орбиты.

Рисунок 30

Скорость планеты при движении ее по орбите тем больше, чем ближе она к Солнцу. В перигелии скорость планеты наибольшая, в афелии наименьшая. Таким образом, второй закон Кеплера количественно определяет изменение скорости движения планеты по эллипсу.

Третий закон Кеплера. Квадраты звездных периодов обращения планет относятся как кубы больших полуосей их орбит.
Если большую полуось орбиты и звездный период обращения одной планеты обозначить через a1,T1, а другой планеты - через а1, Т2, то формула третьего закона будет такова:

Этот закон Кеплера связывает средние расстояния планет от Солнца с их звездными периодами и позволяет установить относительные расстояния планет, от Солнца, поскольку звездные периоды планет уже были вычислены, исходя из синодических периодов, иначе говоря, позволяет выразить большие полуоси всех планетных орбит в единицах большой полуоси земной орбиты.
Большая полуось земной орбиты принята за астрономическую единицу расстояний (а=1 а. е.). Ее значение в километрах было определено позднее, лишь в XVIII в.

Пример решения задачи
Задача. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?

Упражнение 8
1. Марс дальше от Солнца, чем Земля, в 1,5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.
2.Определите период обращения искусственного спутника Земли, если наивысшая точка его орбиты над Землей 5000 км, а наинизшая 300 км. Землю считать шаром радиусом 6370 км. Сравните движение спутника с обращением Луны.

3. Синодический период планеты 500 сут. Определите большую полуось ее орбита и звездный период обращения.

Определение расстояний
и размеров тел
в Солнечной системе

1. Определение расстояний
Среднее расстояние всех планет от Солнца в астрономических единицах можно вычислить, используя третий закон Кеплера. Определив среднее расстояние Земли от Солнца (т. е. значение 1 а. е.) в километрах, можно найти в этих единицах расстояния до всех планет Солнечной системы.
С 40-х годов ХХ века радиотехника позволила определять расстояния до небесных тел посредством радиолокации, о которой вы знаете из курса физики. Советские и американские ученые уточнили радиолокацией расстояния до Меркурия, Венеры, Марса и Юпитера.

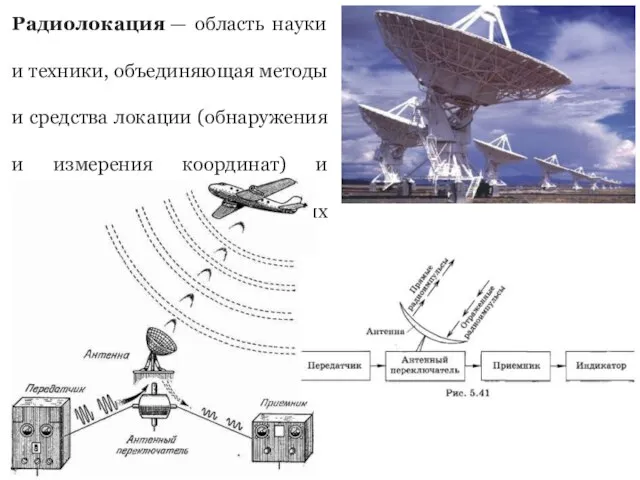
Радиолокация — область науки и техники, объединяющая методы и средства локации (обнаружения и измерения координат) и определения свойств различных объектов с помощью радиоволн.

Вспомните, как по времени прохождения радиолокационного сигнала можно определить расстояние до объекта.

Классическим способом определения расстояний был и остается угломерный геометрический способ. Им определяют расстояния и до далеких звезд, к которым метод радиолокации неприменим. Геометрический способ основан на явлении параллактического смещения.
Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя (рис. 31).

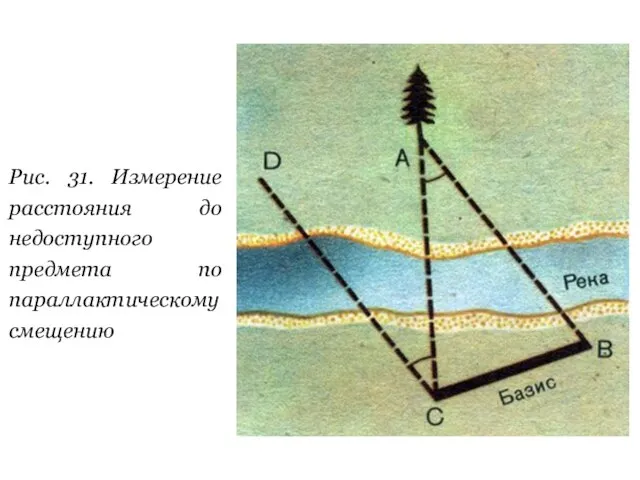
Рис. 31. Измерение расстояния до недоступного предмета по параллактическому смещению

Посмотрите на вертикально поставленный карандаш сначала одним глазом, затем другим. Вы увидите, как он при этом переменил положение на фоне далеких предметов, направление на него изменилось. Чем дальше вы отодвинете карандаш, тем меньше будет параллактическое смещение. Но чем дальше отстоят друг от друга точки наблюдения, т. е. чем больше базис, тем больше параллактическое смещение при той же удаленности предмета. В нашем примере базисом было расстояние между глазами.

Для измерения расстояний до тел Солнечной системы за базис удобно взять радиус Земли. Наблюдают положения светила, например Луны, на фоне далеких звезд одновременно из двух различных пунктов. Расстояние между ними должно быть как можно больше, а соединяющий их отрезок должен составлять с направлением на светило угол, по возможности близкий к прямому, чтобы параллактическое смещение было максимальным. Определив из двух точек А и В (рис. 32) направления на наблюдаемый объект, несложно вычислить угол р, под которым с этого объекта был бы виден отрезок, равный радиусу Земли. Следовательно, чтобы определить расстояния до небесных тел, нужно знать значение базиса - радиуса нашей планеты.

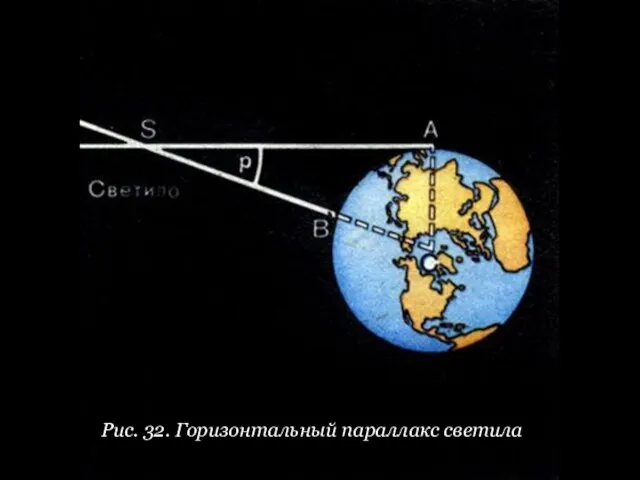
Рис. 32. Горизонтальный параллакс светила

2. Размер и форма Земли
На фотоснимках, сделанных из космоса, Земля выглядит как шар, освещенный Солнцем, и показывает такие же фазы, как Луна (см. рис. 42 и 43).
Рис. 42. Земля над горизонтом Луны

Рис. 43. Фотография Земли, сделанная из космоса

Точный ответ о форме и размере Земли дают градусные измерения, т. е. измерения в километрах длины дуги в 1° в разных местах на поверхности Земли. Этот способ еще в III в, до н. э. применял живший в Египте греческий ученый Эратосфен. Теперь этот способ используется в геодезии - науке о форме Земли и об измерениях на Земле с учетом ее кривизны.
Эратосфен Киренский

На ровной местности выбирают два пункта, лежащие на одном меридиане, и определяют длину дуги между ними в градусах и километрах. Затем вычисляют, скольким километрам соответствует длина дуги, равная 1°. Ясно, что длина дуги меридиана между выбранными точками в градусах равна разности географических широт этих точек: Δφ= = φ1 - φ2. Если длина этой дуги, измеренная в километрах, равна l, то при шарообразности Земли одному градусу (1°) дуги будет соответствовать длина в километрах: Тогда длина окружности земного меридиана L, выраженная в километрах, равна L = 360°n. Разделив ее на 2π, получим радиус Земли.

Одна из наибольших дуг меридиана от Ледовитого океана до Черного моря была измерена в России и в Скандинавии в середине XIX в. под руководством В. Я. Струве (1793-1864), директора Пулковской обсерватории. Большие геодезические измерения в нашей стране выполнены после Великой Октябрьской социалистической революции.
В.Я. Струве

Градусные измерения показали, что длина 1° дуги меридиана в километрах в полярной области наибольшая (111,7 км), а на экваторе наименьшая (110,6 км). Следовательно, на экваторе кривизна поверхности Земли больше, чем у полюсов, а это говорит о том, что Земля не является шаром. Экваториальный радиус Земли больше полярного на 21,4 км. Поэтому Земля (как и другие планеты) вследствие вращения сжата у полюсов.
Шар, равновеликий нашей планете, имеет радиус, равный 6370 км. Это значение принято считать радиусом Земли.

Упражнение 9
Если астрономы могут определять географическую широту с точность до 0,1", то какой максимальной ошибке в километрах вдоль меридиана это соответствует?
Вычислите в километрах длину морской мили, которая равна длине V дуги экватора.

3. Параллакс. Значение астрономической единицы
Угол, под которым со светила виден радиус Земли, перпендикулярный к лучу зрения, называется горизонтальным параллаксом.
Чем больше расстояние до светила, тем меньше угол ρ. Этот угол равен параллактическому смещению светила для наблюдателей, находящихся в точках А и В (см. рис. 32), точно так же как ∠CAB для наблюдателей в точках С и В (см. рис. 31). ∠CAB удобно определять по равному ему ∠DCA, а равны они как углы при параллельных прямых (DCAB по построению).

Расстояние (см. рис. 31-32)
где R - радиус Земли. Приняв R за единицу, можно выразить расстояние до светила в земных радиусах.

Горизонтальный параллакс Луны составляет 57'. Все планеты и Солнце гораздо дальше, и их параллаксы составляют секунды дуги. Параллакс Солнца, например, ρ= 8,8". Параллаксу Солнца соответствует среднее расстояние Земли от Солнца, примерно равное 150 000 000 км. Это расстояние принимается за одну астрономическую единицу (1 а. е.). В астрономических единицах часто измеряют расстояния между телами Солнечной системы.

При малых углах sinρ≈ρ, если угол ρ выражен в радианах. Если ρ выражен в секундах дуги, то вводится множитель где 206265 - число секунд в одном радиане.
Тогда .
Знание этих соотношений упрощает вычисление расстояния по известному параллаксу:

Пример решения задачи
Задача. На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9"?

Упражнение 10
Чему равен горизонтальный параллакс Юпитера, наблюдаемого с Земли в противостоянии, если Юпитер в 5 раз дальше от Солнца, чем Земля?
2. Расстояние Луны от Земли в ближайшей к Земле точке орбиты (перигее) 363 000 км, а в наиболее удаленной точке (апогее) 405 000 км. Определите горизонтальный параллакс Луны в этих положениях.

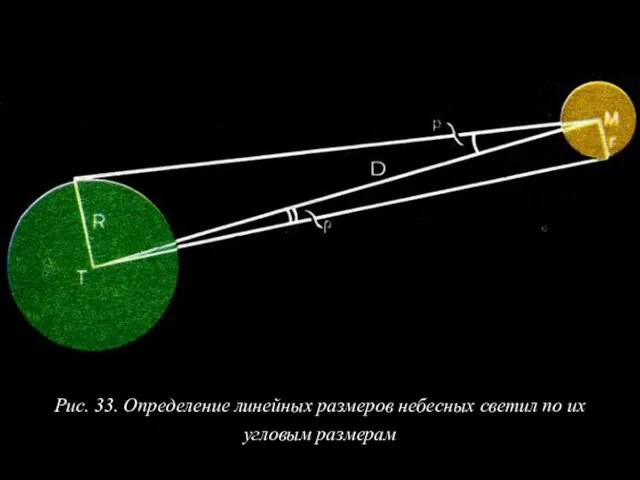
4. Определение размеров светил
На рисунке 33 Т - центр Земли, М - центр светила линейного радиуса r. По определению горизонтального параллакса радиус Земли R виден со светила под углом ρ. Радиус же светила r виден с Земли под углом .Шар, равновеликий нашей планете, имеет радиус, равный 6370 км. Это значение принято считать радиусом Земли.

Рис. 33. Определение линейных размеров небесных светил по их угловым размерам

Поскольку
Если углы и ρ малы, то синусы пропорциональны углам, и можно написать:
Этот способ определения размеров светил применим только тогда, когда виден диск светила. Зная расстояние D до светила и измерив его угловой радиус , можно вычислить его линейный радиус r: r=Dsin или r=D, если угол выражен в радианах.

Пример решения задачи
Задача. Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 0,5°?

Упражнение 11
1. Во сколько раз Солнце больше, чем Луна, если их угловые диаметры одинаковы, а горизонтальные параллаксы соответственно равны 8,8" и 57'?
2. Чему равен угловой диаметр Солнца, видимого с Плутона?
3. Во сколько раз больше получает энергии от Солнца каждый квадратный метр поверхности Меркурия, чем Марса? Нужные данные возьмите из приложений.

5. В каком отношении численно меняется видимый с Земли и с Марса угловой диаметр Солнца от перигелия к афелию, если эксцентриситеты их орбит соответственно равны 0,017 и 0,093?
4. В каких точках небосвода земной наблюдатель видит светило, находясь в точках B и A (рис. 32)?

Задание 5
1. Измерьте транспортиром ∠DCA (рис. 31) и ∠ASC (рис. 32), линейкой - длину базисов. Вычислите по ним соответственно расстояния СА и SC и проверьте результат прямым измерением по рисункам.
2. Измерьте на рисунке 33 транспортиром углы р и И определите по полученным данным отношение диаметров изображенных тел.
3. Определите периоды обращения искусственных спутников, двигающихся по эллиптическим орбитам, изображенным на рисунке 34, измерив их большие оси линейкой и приняв радиус Земли равным 6370 км.