Содержание
- 2. Что такое модель? Модель, в широком смысле любой образ, аналог (мысленный или условный: изображение, описание, схема,
- 3. Что такое моделирование? Моделирование - исследование каких-либо явлений, процессов или систем объектов путем построения и изучения
- 4. Для чего нужна модель? Для понимания строения изучаемого объекта: его структуры, основных свойств, законов развития и
- 5. Приемы и способы моделирования Моделирование Материальное (предметное) Способы моделирования, при которых исследование ведется на основе модели,
- 6. При разработке любой модели необходимо определить объект моделирования, цель моделирования и средства моделирования. В соответствии с
- 7. непрерывные - используют аппарат непрерывной математики, дифференциальных, интегро-дифференциальных уравнений стохастические -основаны на применении вероятностных методов логические
- 8. Процесс построения моделей Формируются основные вопросы о поведении системы, ответы на которые планируется получить с помощью
- 9. Фундаментальная проблема наук о жизни Одной из центральных проблем постгеномной молекулярной биологии и генетики является исследование
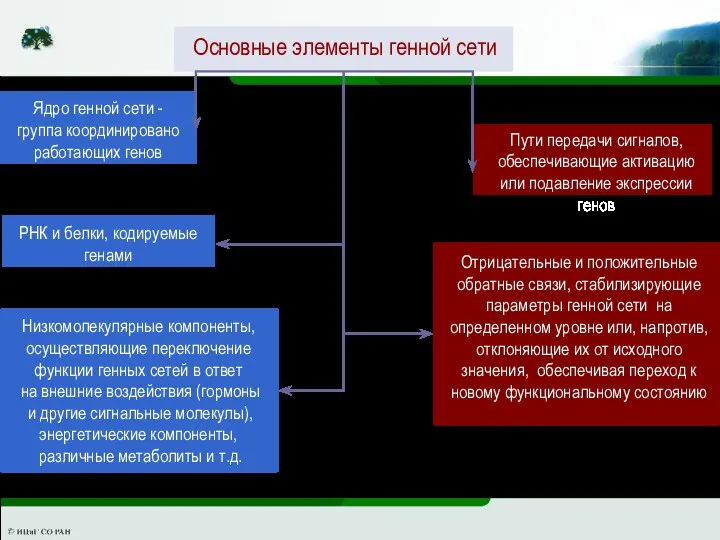
- 10. Генные сети как объект исследования Генная сеть – группа координировано функционирующих генов, контролирующих физиологические, биохимические, молекулярные
- 12. Специфика объекта моделирования Типичные генетические системы состоят из большого количества компонентов различной природы и структурно-функциональной организации,
- 13. Специфика объекта моделирования Биологические системы является самовоспроизводящимися динамическими системами. Особенностью функционирования биологических систем во времени является
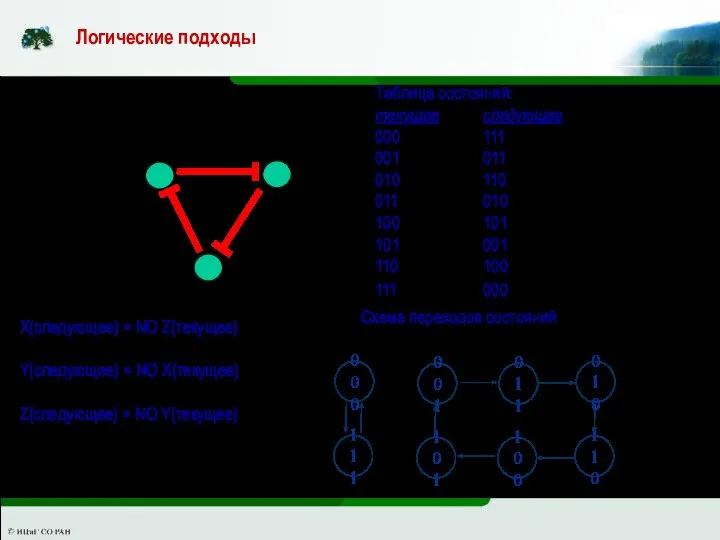
- 14. Логические подходы Логические подходы основаны на применении для описания механизмов в терминах логики и дискретной математики.
- 15. Логические подходы X Z Y X(следующее) = NO Z(текущее) Y(следующее) = NO X(текущее) Z(следующее) = NO
- 16. Стохастическое моделирование В стохастических моделях молекулярные события описываются как случайные процессы. В них каждое элементарное событие
- 17. Стохастическое моделирование В стохастическом подходе с непрерывным временем считается, что система из текущего момента времени переходит
- 18. Непрерывные подходы к описанию биологических систем Динамика молекулярно-генетических систем в непрерывных моделях формально описывается системами дифференциальных
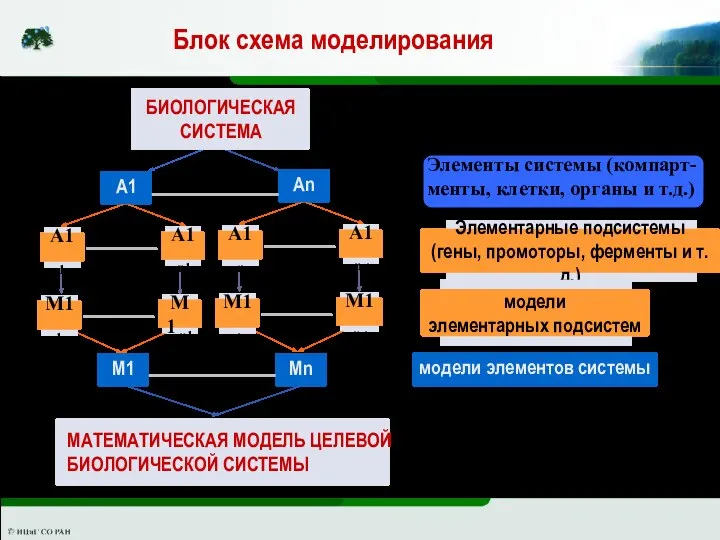
- 19. Иерархический метод моделирования ИММ использует в качестве основного подхода принцип иерархической декомпозиции целевой биологической системы до
- 20. Элементы системы (компарт- менты, клетки, органы и т.д.) Блок схема моделирования
- 21. Какие подсистемы считаются элементарными? Элементарной подсистемой моделируемой системы считается подсистема, которая может быть рассмотрена автономно, вне
- 22. Примерный список элементарных подсистем генных сетей. При этом следует помнить, что обычно элементарные подсистемы с биохимической
- 23. В таблице мы привели примерный список элементарных подсистем. Список не претендует на полноту. Не все приведенные
- 24. Общий вид элементарных моделей X - вектор управляемых переменных, Y - вектор управляющих переменных, K –
- 25. Методы реконструкции моделей элементарных подсистем
- 26. Биохимическая природа молекулярно-генетических процессов - основа для вывода функции V Фундаментальной основой для вывода функции V
- 27. Кинетический закон действующих масс выводится на основе теории соударений. Пусть имеется биохимическая реакция A + B
- 28. Если имеется конкретная биохимическая схема реакций вида (1), то мгновенная скорость изменения концентрации любого вещества равняется
- 29. Теорема Корзухина – теоретическая основа для применения химико-кинетического подхода к моделированию молекулярно-генетических систем (не строгая формулировка)
- 30. Значение теоремы Корзухина. При использовании химико-кинетическиого подхода V является полиномом степени не выше двух. Однако на
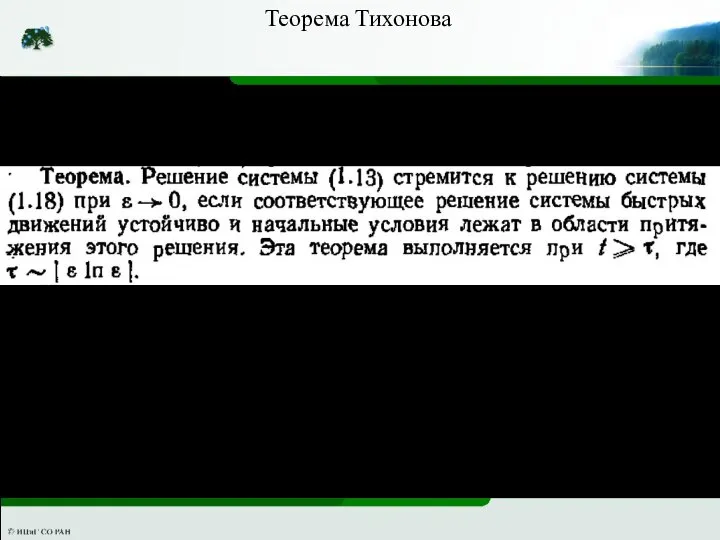
- 31. Теорема Тихонова Пусть дана система дифференциальных автономных уравнений
- 32. Теорема Тихонова
- 33. Теорема Тихонова позволяет понижать порядок системы дифференциальных уравнений. Для того чтобы применить этот метод к биохимической
- 34. Формула Михаэлиса-Ментен Простейшие преобразования и переход к исходным обозначениям дает знаменитую формулу Пример применения теоремы Тихонова
- 35. Разделение процессов на быстрые и медленные. Как уже говорилось, общего алгоритма разделения переменных на быстрые и
- 36. Квазистационарный метод исключения переменных (метод Кинга-Альтмана)
- 37. Важный частный случай применения принципа квазистационарности для исследования механизмов ферментативных реакций Основу принципа квазистационарности составляет рассмотрение
- 38. Пусть имеется фермент E, который может пребывать в n состояниях: ei, i=1,…,n. Пусть из i-го состояния
- 39. Метод Кинга-Альтмана
- 40. Метод Кинга-Альтмана
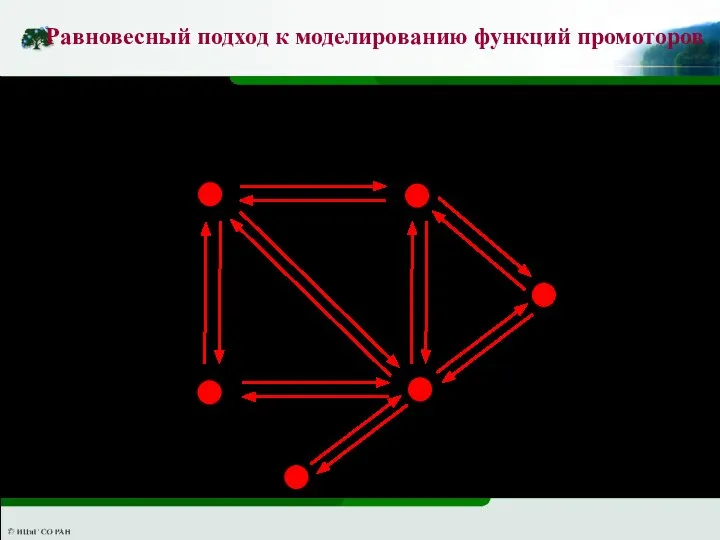
- 41. Равновесный подход к моделированию функций промоторов
- 42. Равновесный подход к моделированию функций промоторов g gA gP gR gAR gAP
- 43. Приравняем к нулю правую часть системы и учтем уравнение баланса Равновесный подход к моделированию функций промоторов
- 44. Итоговые формулы элементарной модели функционирования гипотетического промотора Равновесный подход к моделированию функций промоторов
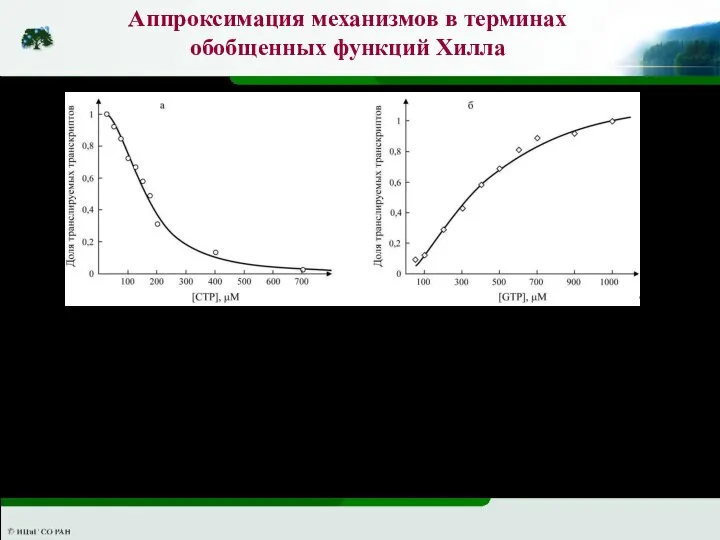
- 45. Аппроксимация механизмов в терминах обобщенных функций Хилла Теперь перейдем к рассмотрению подхода, который используется для моделирования
- 46. Аппроксимация механизмов в терминах обобщенных функций Хилла ОФХ являются естественным расширением класса рациональных полиномов, которые возникают
- 47. Аппроксимация механизмов в терминах обобщенных функций Хилла Регуляция экспрессии гена pyrC в клетке E.coli Экспрессия гена,
- 48. Аппроксимация механизмов в терминах обобщенных функций Хилла Регуляция экспрессии гена pyrC в клетке E.coli Таким образом,
- 49. Аппроксимация механизмов в терминах обобщенных функций Хилла
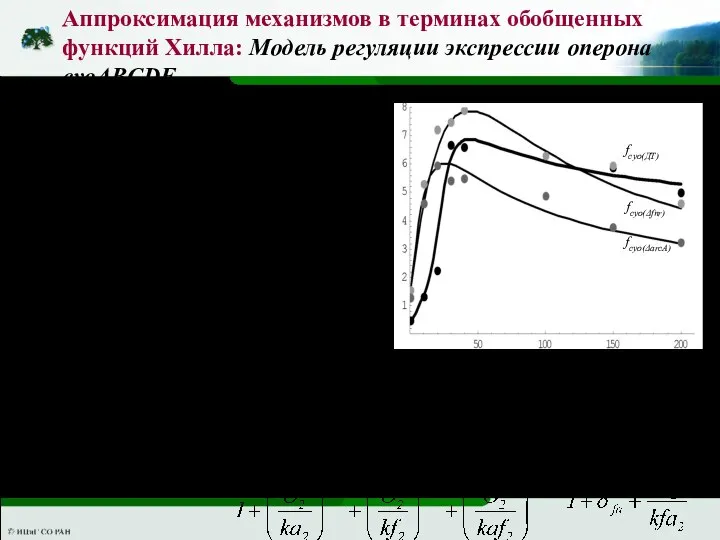
- 50. Аппроксимация механизмов в терминах обобщенных функций Хилла Модель регуляции экспрессии оперона cyoABCDE Структура промотора оперона cyoABCDE,
- 51. Аппроксимация механизмов в терминах обобщенных функций Хилла Регуляция экспрессии гена pyrC в клетке E.coli
- 52. Аппроксимация механизмов в терминах обобщенных функций Хилла: Модель регуляции экспрессии оперона cyoABCDE Зависимость уровня транскрипции оперона
- 53. Аппроксимация механизмов в терминах обобщенных функций Хилла Сделаем несколько комментариев к рассмотренной модели экспрессии оперона cydAB.
- 54. 1. Рациональный полином 3. Функция, которая может быть получена из ОФХ, путем подстановки в нее вместо
- 55. A ⎯→ B, a = [A], b = [B] k -da/db = db/dt = ka e=[E],
- 56. Закон суммирования локальных скоростей элементарных подсистем
- 57. Закон суммирования локальных скоростей элементарных подсистем
- 59. Скачать презентацию












































![A ⎯→ B, a = [A], b = [B] k -da/db =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/950867/slide-54.jpg)


 Строение и функции листа
Строение и функции листа Бионеорганическая химия. Особенности биохимический процессов. (Лекция 1)
Бионеорганическая химия. Особенности биохимический процессов. (Лекция 1) Презентация на тему Какие разные – братья наши меньшие! 6 класс
Презентация на тему Какие разные – братья наши меньшие! 6 класс 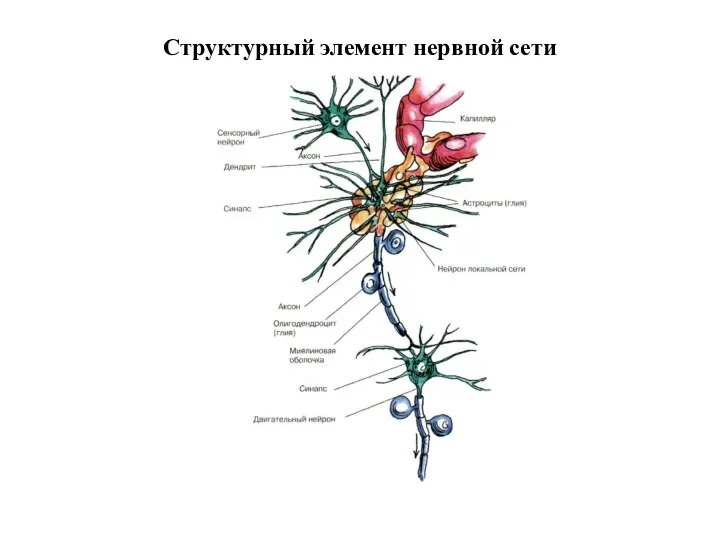 Структурный элемент нервной сети
Структурный элемент нервной сети Презентация на тему Эволюция млекопитающих
Презентация на тему Эволюция млекопитающих  Лимфатическая система человека. (Лекция 7)
Лимфатическая система человека. (Лекция 7) Покриви тіла тварин
Покриви тіла тварин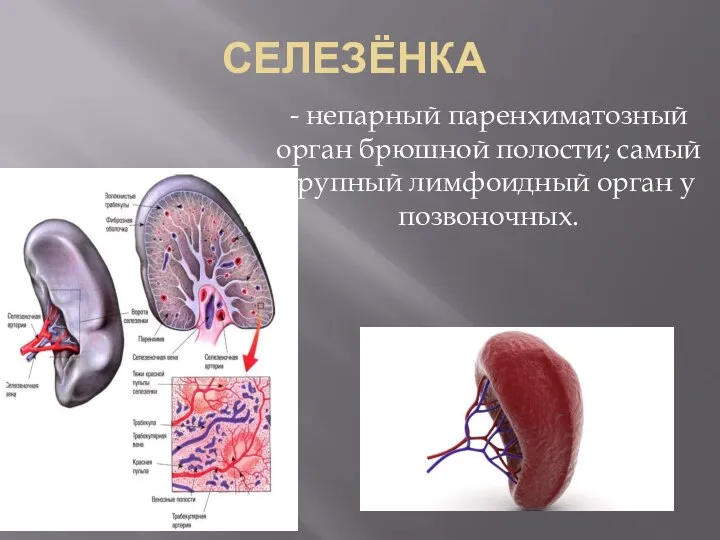 Селезёнка
Селезёнка Регуляция клеточного цикла
Регуляция клеточного цикла Регуляция дыхания. ФУС поддержания постоянства газов в крови
Регуляция дыхания. ФУС поддержания постоянства газов в крови Živočíchy - vylučovanie
Živočíchy - vylučovanie День тигра
День тигра Потомок больших голубых котов – вислоухий британец Луксор
Потомок больших голубых котов – вислоухий британец Луксор Неандерталец. Антропогенез. Эволюция человека. Часть 7
Неандерталец. Антропогенез. Эволюция человека. Часть 7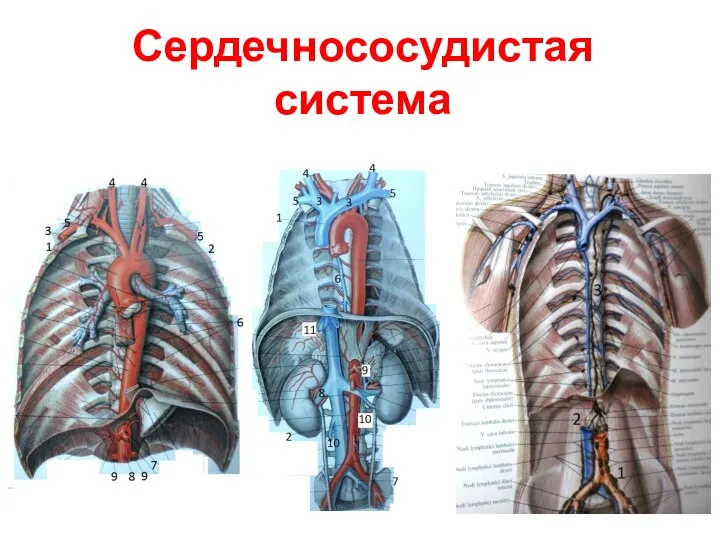 Сердечно-сосудистая система человека. (Лекция 4)
Сердечно-сосудистая система человека. (Лекция 4) Способы деления клеток: амитоз, митоз и мейоз
Способы деления клеток: амитоз, митоз и мейоз Разнообразие животных. Беспозвоночные животные
Разнообразие животных. Беспозвоночные животные Подцарство Многоклеточные, общие признаки. Происхождение
Подцарство Многоклеточные, общие признаки. Происхождение Пищеварение в желудке и кишечнике
Пищеварение в желудке и кишечнике Основы морфологии бактерий
Основы морфологии бактерий Возрастные особенности человека
Возрастные особенности человека Презентация на тему Круглые черви
Презентация на тему Круглые черви  10 кл.Белки
10 кл.Белки Нейрофизиология высших отделов ЦНС. Лекция 1
Нейрофизиология высших отделов ЦНС. Лекция 1 2_Kletochnaya_teoria
2_Kletochnaya_teoria Фитоиммунология. Пассивный и активный иммунитет
Фитоиммунология. Пассивный и активный иммунитет Самое прекрасное создание природы!
Самое прекрасное создание природы! Введение в нейроанатомию. Развитие спинного и головного мозга. Классификация нервной системы: центральная и периферическая части
Введение в нейроанатомию. Развитие спинного и головного мозга. Классификация нервной системы: центральная и периферическая части