Механические свойства грунта

Схема испытания грунта на срез (сдвиг):
а – начало испытания, б – окончание испытания; 1 – грунт, 2 и 3 – соответственно верхнее подвижное и нижнее неподвижное кольца, 4 – диск, передающий вертикальную нагрузку (штампик)

Деформативностью грунта называют его способность деформироваться под нагрузкой без разрушения (без образования в нем поверхностей скольжения). Зависимость деформаций ε от напряжений σ в грунте криволинейна, но при небольших напряжениях ее можно считать линейной. Расчеты деформаций основания производятся, как правило, только для первой фазы, когда деформации можно считать линейными. На это ориентированы нормативные документы по расчету оснований.
Деформативность грунта в этой фазе оценивается харакдвумя теристиками. Это модуль деформации Е, характеризующий связь деформаций ε с напряжениями σ, и коэффициент поперечной деформации (коэффициент Пуассона) ν, характеризующий отношение поперечных деформаций εпоп к продольным εпрод.

За рубежом большинство специалистов считает статическое зондирование чисто эмпирическим методом, т.е. методом, не имеющим теоретической основы. Такая точка зрения возникла из-за многочисленных неудач получения теоретического решения задачи о проникании зонда в идеализированную среду, моделирующую реальный грунт. Всякий раз при решении таких задач исследователи сталкивались с исключительными математическими трудностями, которые удавалось преодолеть за счет упрощения исходных данных и многочисленных допущений.
В качестве модели грунта принималась линейно-деформирующаяся среда или идеально сыпучая среда, но ничего полезного это не давало.
В ХХ веке были опубликованы десятки теоретических статей на эту тему, но все получаемые результаты оказывались далекими от реальности. Реальность отображали только эмпирические зависимости, причем по-разному в разных регионах

При использовании в качестве модели грунта сыпучей среды получались зависимости типа qc =f (φ, c), при модели линейно-деформируемой среды –зависимости qc =f (Е), где φ, c, Е – соответственно угол внутреннего трения, удельное сцепление, модуль деформации грунта. В реальных условиях эти зависимости подтверждались плохо, причем фактическая связь qc со свойствами грунта была различной в каждом генетическом типе грунта. Таким образом, в теоретическом направлении образовался тупик.
Выход был найден в нашей стране в 60-е годы ХХ века. В качестве модели грунта была принята упруго-пластическая среда, способная деформироваться линейно (по закону Гука) и разрушаться в соответствии с законом Кулона. Задача о проникании зонда в такую среду была математически неразрешимой, но выходом оказалось использование идеи, высказанной К. Терцаги 20-е годы ХХ века. Он заметил, что напряженное состояние грунта вокруг зонда почти такое же, как и вокруг расширяющейся цилиндрической скважины от радиуса r = 0 до r = ro (где ro – радиус зонда). Такая задача (о расширяющейся скважине) была решена еще вначале ХХ века, в связи с чем в описанной постановке задача сводилась к использованию уже известных решений, перестроенных на новые условия – погружение зонда.

Схема проникания зонда в упруго-пластическую среду:
а – горизонтальное сечение грунта, окружающего зонд (ro – радиус наконечника зонда, ρ – радиус области предельного равновесия); б – схема сил, действующих на конус (qт и qn – части общего удельного сопротивления грунта, отражающие соответственно трение на поверхности конуса и деформации окружающего грунта)

Решение рассматриваемой задачи было получено в 60-х годах, тогда же и опубликовано. Это была «смешанная задача» теории упругости и теории предельного равновесия. Решение было сложным и очень громоздким (как все решения в этих областях механики). В обобщенном виде оно имело следующий вид:

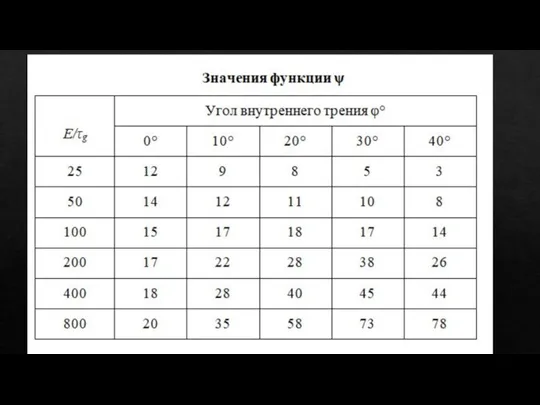
Угол внутреннего трения грунта φ при высоких нормальных напряжениях близких к qс; для глин, суглинков, супесей может приниматься равным нулю, для песков, гравия он не снижается. По этой причине величина β в формуле (3а) у глинистых грунтов будет равна 1, для песчаных вычисляется по формуле (3 а) в зависимости от φ или принимается по табл. 2;