Содержание
- 2. Использование ЭВМ для оптимизации процессов биосинтеза продуктов метаболизма на основе моделей их кинетики является самой распространенной
- 3. Два важных направления использования математической модели в ходе оперативного управления микробиологическим процессом: Модель и ее константы
- 4. Модель используют для расчета оптимальных условий всех параметров, входящих в нее. Если же часть параметров модели
- 5. Математическое моделирование микробиологических процессов показывает, что наиболее приемлемые для использования относительно простые математические модели характеризуются «константами»,
- 6. Второе направление управления процессом: ЭВМ не просто рассчитывает оптимальные режимы, но и на основе текущей информации
- 7. Наиболее важные управляемые параметры процесса: Концентрации лимитирующего субстрата; величина рН Другие параметры процесса: Концентрация биомассы; концентрация
- 8. Таким образом, возможность корректировки математической модели в ходе процесса существенно ограничена объемом информации, которую можно получить
- 9. Адаптивное управление режимом аэрации – перемешивания Алгоритм перемешивания на основе математической модели процесса ферментации основан на
- 10. В качестве математической модели процесса используется зависимость интенсивности дыхания от концентрации растворенного кислорода на основе механизма
- 11. r - размер (радиус) агломерата («жидкой частицы»); N – мощность, определяется как сумма мощностей, затрачиваемых на
- 12. Уравнение 6, 7, 8, 9 К-коэффициент мощности, ŋ -коэффициент снижения мощности, потребляемой мешалкой в аэрируемой жидкости
- 13. С - концентрацию растворенного кислорода; С* - равновесная концентрация кислорода (принята пропорциональной парциальному давлению кислорода во
- 14. Пусть G=const, скорость вращения мешалки n – единственное управляющее воздействие. Решение задачи оценки оптимального значения скорости
- 15. Уравнение 13 Коэффициенты A и α находятся из системы уравнений типа (10): А коэффициенты Qm и
- 16. Величина nопт определяется путем подстановки величины Q в уравнение (12) с учетом уравнений (1), (5) и
- 17. Алгоритм решения данной задачи на ЭВМ включает следующие этапы. Расчет интенсивности дыхания Qi по текущей информации.
- 18. Найденная величина сравнивается со значением Q, до нанесения возмущения ∆n. Если относительная разность не превышает величины
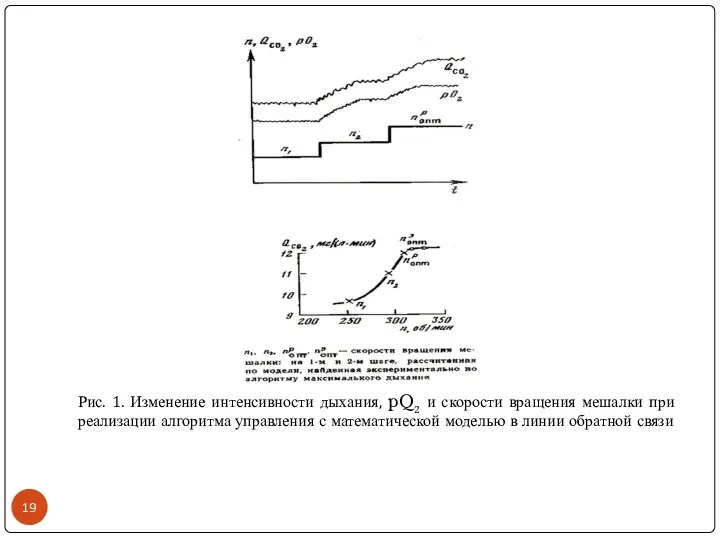
- 19. Рис. 1. Изменение интенсивности дыхания, pQ2 и скорости вращения мешалки при реализации алгоритма управления с математической
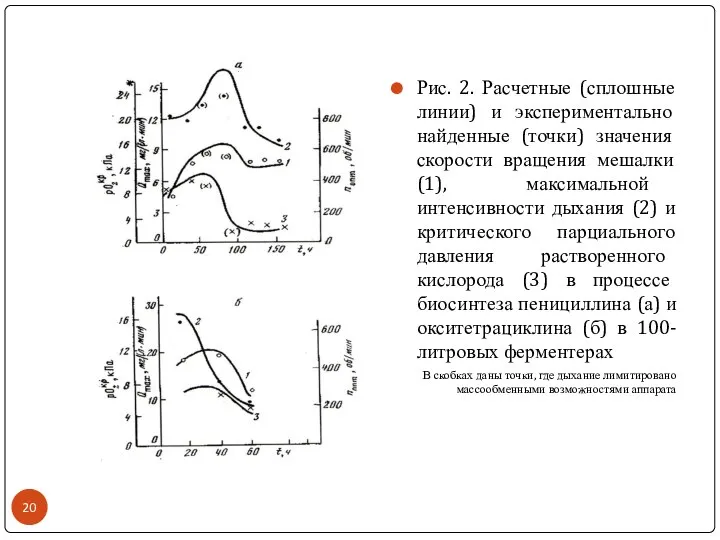
- 20. Рис. 2. Расчетные (сплошные линии) и экспериментально найденные (точки) значения скорости вращения мешалки (1), максимальной интенсивности
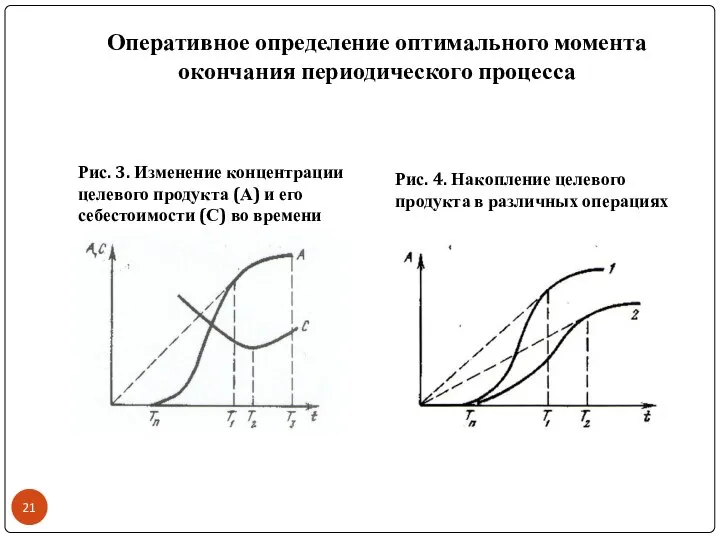
- 21. Оперативное определение оптимального момента окончания периодического процесса Рис. 3. Изменение концентрации целевого продукта (А) и его
- 23. Скачать презентацию

















 Птицы Рязанской области
Птицы Рязанской области Презентация на тему ВСТРЕЧА ЕВРОПЫ И АМЕРИКИ
Презентация на тему ВСТРЕЧА ЕВРОПЫ И АМЕРИКИ  Ткани расстений
Ткани расстений Витамин D (кальциферол)
Витамин D (кальциферол) Море и морские обитатели
Море и морские обитатели Презентация на тему Надотряд Скаты
Презентация на тему Надотряд Скаты 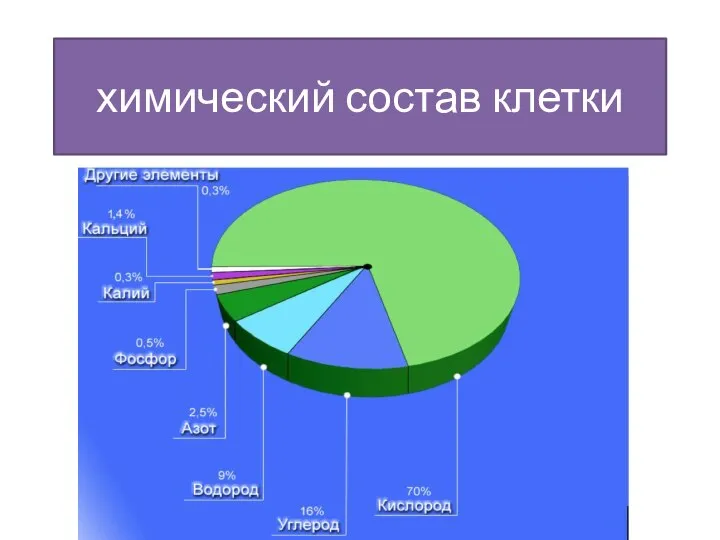 Химический состав клетки
Химический состав клетки Жизненная емкость легких
Жизненная емкость легких Живые организмы как среда обитания
Живые организмы как среда обитания Предпосылки возникновения учения Ч. Дарвина
Предпосылки возникновения учения Ч. Дарвина Грибы съедобные и несъедобные
Грибы съедобные и несъедобные Урок чистой воды. Российский водный пирог
Урок чистой воды. Российский водный пирог Эволюция нервной системы
Эволюция нервной системы Генетико-прогностическое описание систем
Генетико-прогностическое описание систем Вакуоль в растительной клетке
Вакуоль в растительной клетке Систематика и классификация микроорганизмов
Систематика и классификация микроорганизмов Цитология растений. Вегетативные органы растений
Цитология растений. Вегетативные органы растений Контрольные задания по биологии
Контрольные задания по биологии Количество хромосом и молекул ДНК в разные фазы митоза и мейоза
Количество хромосом и молекул ДНК в разные фазы митоза и мейоза Ліпіди
Ліпіди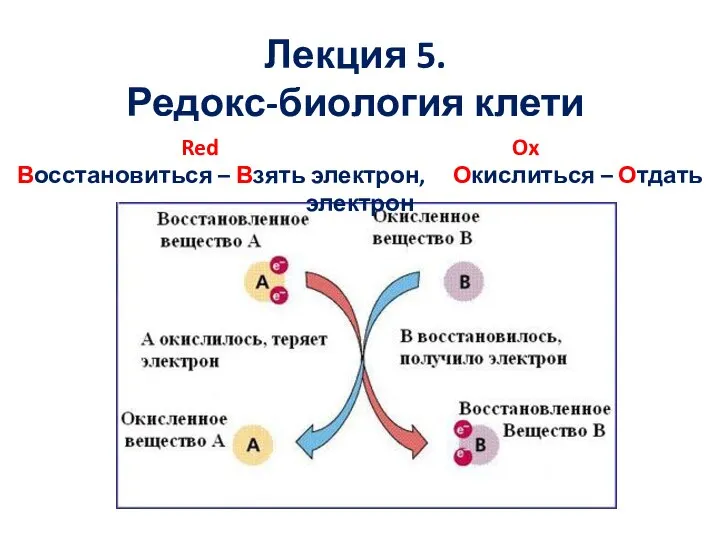 Редокс биология клетки
Редокс биология клетки Возрастные особенности человека
Возрастные особенности человека Отруйні гриби
Отруйні гриби Биосфера
Биосфера Развитие мышечной системы в онтогенезе
Развитие мышечной системы в онтогенезе Особенности, многообразие и классификация животных. 7 класс
Особенности, многообразие и классификация животных. 7 класс Выращивание тропических фруктов из косточки
Выращивание тропических фруктов из косточки Витамин В6
Витамин В6