Закономерности роста и размножения клеток. Скорость растущей биомассы клеток и даваемый ею прирост

СКОРОСТЬ РОСТА КЛЕТОК
При исследовании ростовых процессов нужно различать растущую биомассу клеток и даваемой ею прирост.
Иногда прирост сразу же отделяется от клетки и биомасса последней не увеличивается.
Примером может служить процесс отшнуровывания покоящихся спор (конидий) на конце особой цилиндрической клетки (стеригмы) у грибов-пенициллов (рисунок 1,2).

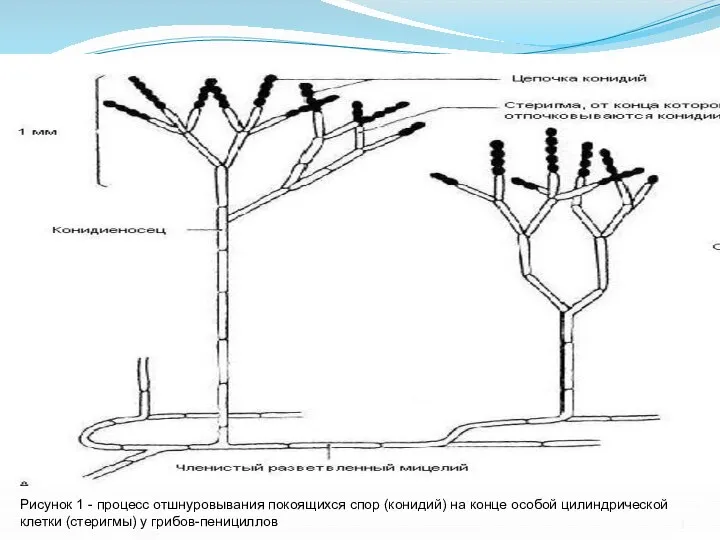
Рисунок 1 - процесс отшнуровывания покоящихся спор (конидий) на конце особой цилиндрической клетки (стеригмы) у грибов-пенициллов

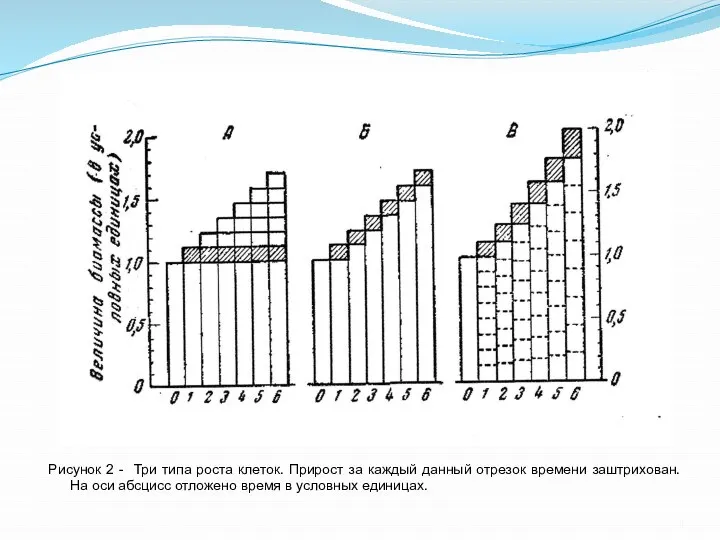
Рисунок 2 - Три типа роста клеток. Прирост за каждый данный отрезок времени заштрихован. На оси абсцисс отложено время в условных единицах.

Для количественной характеристики ростовых процессов пользуются двумя показателями:
1) абсолютной (валовой) и
2) относительной (удельной) скоростью роста.
Валовая (общая) скорость роста (v) характеризуется абсолютным приростом биомассы за единицу времени (обычно – за 1 час). В дифференциальной форма она выражается уравнением:
где dm обозначает приращение микробной биомассы за бесконечно малый отрезок времени dt.

Средняя удельная скорость роста (μср) за какой-либо период времени
t1 - t0 равна:

Относительная скорость роста характеризуется увеличением натуральных логарифмов биомассы за единицу времени.
Этим она отличается от валовой скорости роста, которая изменяется приростом абсолютных величин биомассы.
С течением времени роста может оставаться постоянной, увеличиваться или убывать. Соответственно этому ростовой процесс может иметь равномерный, ускоряющий или затухающий характер.

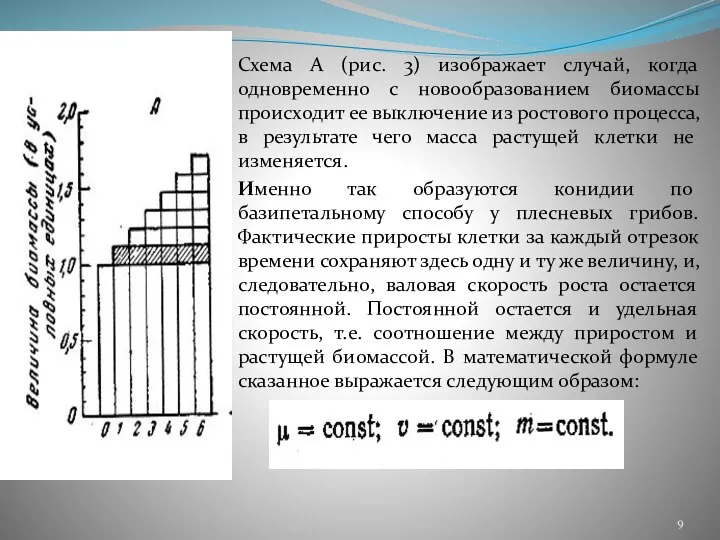
Схема А (рис. 3) изображает случай, когда одновременно с новообразованием биомассы происходит ее выключение из ростового процесса, в результате чего масса растущей клетки не изменяется.
Именно так образуются конидии по базипетальному способу у плесневых грибов. Фактические приросты клетки за каждый отрезок времени сохраняют здесь одну и ту же величину, и, следовательно, валовая скорость роста остается постоянной. Постоянной остается и удельная скорость, т.е. соотношение между приростом и растущей биомассой. В математической формуле сказанное выражается следующим образом:

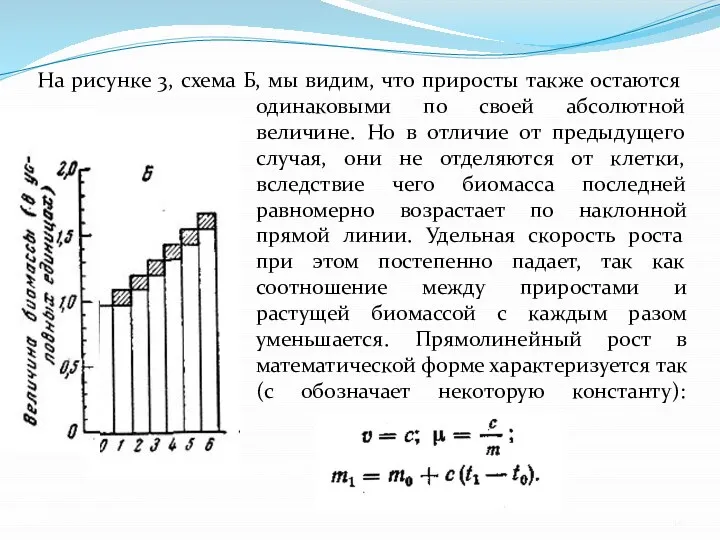
На рисунке 3, схема Б, мы видим, что приросты также остаются одинаковыми по своей абсолютной величине. Но в отличие от предыдущего случая, они не отделяются от клетки, вследствие чего биомасса последней равномерно возрастает по наклонной прямой линии. Удельная скорость роста при этом постепенно падает, так как соотношение между приростами и растущей биомассой с каждым разом уменьшается. Прямолинейный рост в математической форме характеризуется так (с обозначает некоторую константу):

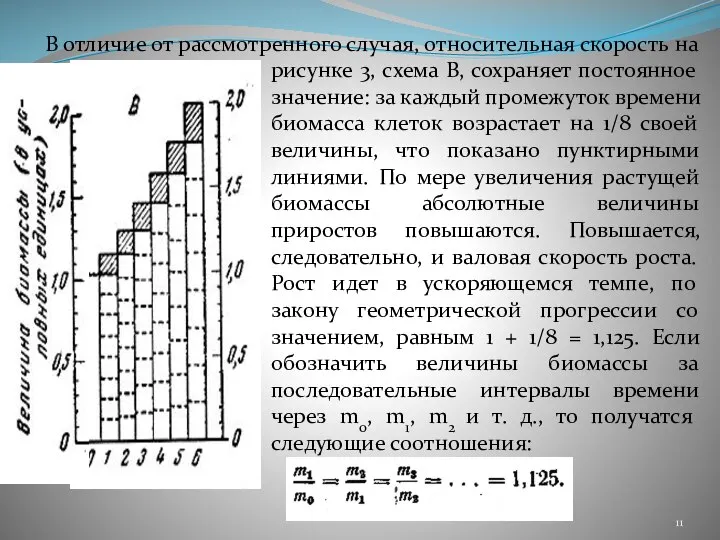
В отличие от рассмотренного случая, относительная скорость на рисунке 3, схема В, сохраняет постоянное значение: за каждый промежуток времени биомасса клеток возрастает на 1/8 своей величины, что показано пунктирными линиями. По мере увеличения растущей биомассы абсолютные величины приростов повышаются. Повышается, следовательно, и валовая скорость роста. Рост идет в ускоряющемся темпе, по закону геометрической прогрессии со значением, равным 1 + 1/8 = 1,125. Если обозначить величины биомассы за последовательные интервалы времени через m0, m1, m2 и т. д., то получатся следующие соотношения:

Рост с постоянной удельной скоростью в общей форме характеризуется так:
Здесь с – некоторый постоянный коэффициент, а е = 2,714… - основание натуральных логарифмов.
Такой рост называют «экспоненциальным», поскольку независимая переменная (время) стоит в экспоненте (показателе степени).
Уравнение роста после логарифмирования превратится в уравнение прямой:
Откладывая на графике логарифмы биомассы, мы получим прямую наклонную линию.

Необходимо подчеркнуть, что не всякий ускоряющийся рост подчиняется закону геометрической прогрессии.
Это бывает только в том частном случае, когда удельная скорость роста сохраняет строго постоянное значение.
При повышающейся, равно как и при слегка убывающей удельной скорости, рост также идет в ускоряющемся темпе, по изогнутой кверху кривой, однако формула геометрической прогрессии в этих случаях непригодна.
Например, при переходе клетки от состояния физиологического покоя к активной жизнедеятельности (в частности, при прорастании бактериальных спор) удельная скорость роста постепенно увеличивается, в связи с чем, кривая нарастания клеточной биомассы очень круто изгибается вверх.

Бактериальная клетка в физиологически активном состоянии растет всей массой своего тела (в этом состоит ее отличие от мицелиальных организмов).
Поэтому можно было бы ожидать, что по мере увеличения размеров клетки ее приросты будут повышаться в геометрической прогрессии, согласно вышеуказанному экспоненциальному закону.
Это в действительности и наблюдается у палочковидных бактерий, клетки которых увеличиваются только в длину, поперечник же их в процессе роста, остается постоянным, в связи с чем, соотношение между поверхностью и объемом клетки почти не меняется.

Иное наблюдается у шаровидных бактерий. На скорость их роста существенное влияние оказывает изменяющееся соотношение между поверхностью клетки, через которую последняя получает питательные вещества, и ее объемом. Поверхность возрастает пропорционально квадратной степени радиуса, а объем – пропорционально его кубу. Поэтому по мере увеличения поперечника растущей клетки соотношение между поверхностью и объемом падает. Это ведет к ухудшению условий обмена веществ и затуханию скорости роста.

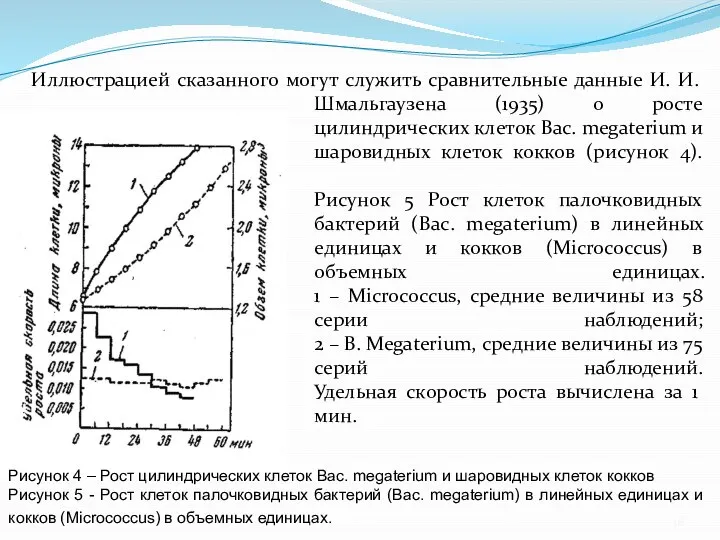
Иллюстрацией сказанного могут служить сравнительные данные И. И. Шмальгаузена (1935) о росте цилиндрических клеток Вac. megaterium и шаровидных клеток кокков (рисунок 4).
Рисунок 5 Рост клеток палочковидных бактерий (Bac. megaterium) в линейных единицах и кокков (Micrococcus) в объемных единицах.
1 – Micrococcus, средние величины из 58 серии наблюдений; 2 – В. Megaterium, средние величины из 75 серий наблюдений. Удельная скорость роста вычислена за 1 мин.
Рисунок 4 – Рост цилиндрических клеток Вac. megaterium и шаровидных клеток кокков
Рисунок 5 - Рост клеток палочковидных бактерий (Bac. megaterium) в линейных единицах и кокков (Micrococcus) в объемных единицах.

Рост клеток протозоа и водорослей обычно имеет такой же затухающий характер, как и у кокковых бактерий.
Но в данном случае решающую роль играет не столько соотношение между поверхностью и объемом, сколько цикл ядерных превращений.
Сразу после обособления клетки происходит быстрое нарастание ее цитоплазмы.
Затем наступает вторая фаза развития, в течение которой протекает деление клеточного ядра. В эту фазу рост клетки резко тормозится.

В случае постепенного падения удельной скорости роста в ростовом процессе может иметь замедляющийся, равномерный или даже слегка ускоряющийся характер. При постоянной или повышающейся удельной скорости он имеет всегда только ускоряющийся характер.

СКОРОСТЬ РАЗМНОЖЕНИЯ КЛЕТОК
О скорости размножения одноклеточных организмов судят по тому, как часто они делятся или почкуются.
Отрезок времени, в течение которого обособившаяся молодая клетка вырастает до максимальной величины и приступает в свою очередь к делению (или, соответственно, почкованию) называется «продолжительностью генерации».
Надо заметить, что сроки повторения актов деления и почкования довольно постоянны.
Как показывают прямые микроскопические наблюдения, они заметно различаются не только у соседних клеток, но и у потомков одной и той же клетки.
Поэтому на практике обычно приходится иметь дело со средней продолжительностью генерации (g)

Предположим, что вначале было N0 клеток. За каждую генерацию численность их повышается в 2 раза, а за n генераций она возрастает в 2n раз и достигает величины N1:
Прологарифмировав это уравнение и сделав надлежащие перестановки, получим формулу, необходимую для вычисления количества клеток поколений, сменившихся за данный период времени t1 - t0:
Скорость размножения (v) характеризуется средним числом делений или почкований каждой клетки за единицу времени. С этой целью общее количество поколений (n) делят на время (t1 - t0):
Коэффициент размножения (v) не всегда бывает целым числом. Когда, например, продолжительность генерации выходит за пределы 1 часа, он выражается дробью меньше единицы.

Если, как было сказано выше, за отрезок времени t1 - t0, сменяется n клеточных поколений. То продолжительность одного поколения (генерации) в среднем составляет:
Подставив сюда вместо v предыдущее выражение, получим формулу для вычисления средней продолжительности генерации:
В процессе своего индивидуального развития клетка значительно увеличивается в размерах, однако после каждого очередного деления или почкования она возвращается в исходное состояние. Благодаря этому размеры клеток регулярно колеблются вокруг некоторого среднего уровня, не выходя за пределы известных границ.

В популяциях, где одновременно присутствуют клетки, находящиеся на разных ступенях индивидуального развития, средний вес одной клетки остается постоянным (конечно, лишь до тех пор, пока не изменится состав окружающей среды, что повлечет за собой измельчение или, наоборот, укрупнение клеток). Поэтому суммарный вес биомассы культуры бывает прямо пропорционален численности клеток: m = a – N (где a – средний вес одной клетки).

На этом основании величины N1 и N0 можно заменить, соответственно, на m1 и m0 (коэффициент а при этом сокращается):
Подобную же замену можно произвести в уравнении, характеризующем скорость размножения клеток:
Таким образом, для вычисления продолжительности генерации и скорости размножения клеток необязательно определять их численность – иногда можно ограничиться измерением суммарной биомассы культуры.

О скорости роста микроорганизмов принято судить по продолжительности генерации.
Указанный прием достаточно обоснован, поскольку удельная скорость роста и время генерации находятся между собой в обратной пропорциональной зависимости. Следует, однако, предостеречь против излишнего увлечения понятием «продолжительность генерации».
Это понятие, безусловно, приложимо только к одноклеточным организмам, размножающимся путем деления или почкования. По отношению же к мицелиальным организмам (например, актиномицетам) оно лишено реального смысла.
Вопрос о том, за какой срок длина гиф удваивается, представляет не больший интерес, чем вопрос о времени их удлинения, скажем, в полтора или три раза.

Кроме того, нужно учитывать, что удвоение биомассы на протяжении одной генерации вовсе не означает, что ее относительный прирост за это время равен единице.
Расчеты, построенные на таком допущении, ведут к серьезным ошибкам. Скорость размножения только пропорциональна, но не равна относительной скорости роста. Если, например, клетка делится 1 раз за час (v=1), то μ=0,693 и, следовательно, относительный прирост исходной биомассы за 1 час составляет только 0,693.
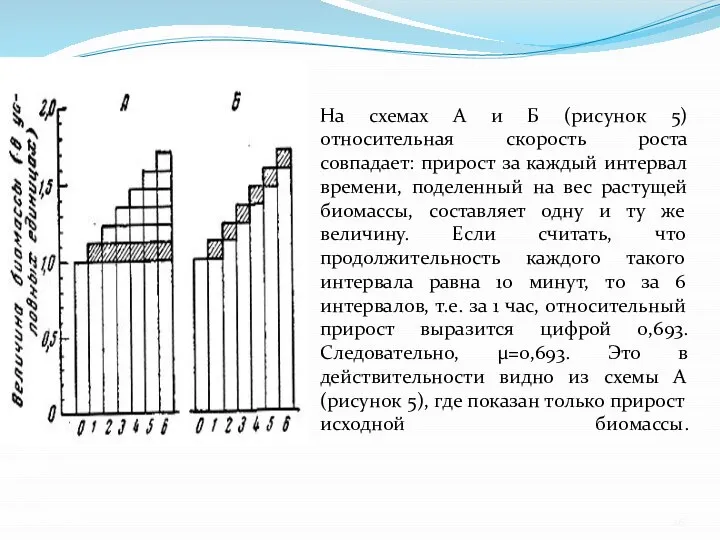
Если клетка делится дважды в течение часа (v=2), то относительная скорость роста биомассы составляет 1,386.

На схемах А и Б (рисунок 5) относительная скорость роста совпадает: прирост за каждый интервал времени, поделенный на вес растущей биомассы, составляет одну и ту же величину. Если считать, что продолжительность каждого такого интервала равна 10 минут, то за 6 интервалов, т.е. за 1 час, относительный прирост выразится цифрой 0,693. Следовательно, μ=0,693. Это в действительности видно из схемы А (рисунок 5), где показан только прирост исходной биомассы.

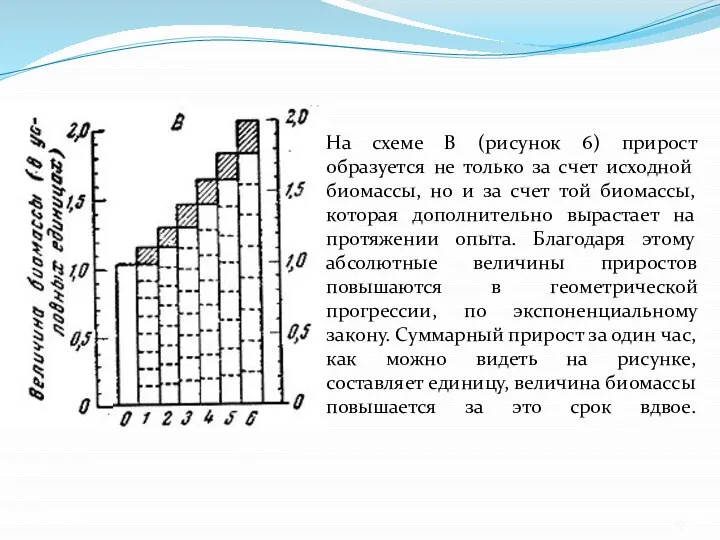
На схеме В (рисунок 6) прирост образуется не только за счет исходной биомассы, но и за счет той биомассы, которая дополнительно вырастает на протяжении опыта. Благодаря этому абсолютные величины приростов повышаются в геометрической прогрессии, по экспоненциальному закону. Суммарный прирост за один час, как можно видеть на рисунке, составляет единицу, величина биомассы повышается за это срок вдвое.