Содержание
- 2. (7.1) Наилучшая линейная процедура получения оценок параметров уравнения (7.1) и условия, при которых эта процедура дает
- 3. Карл Фридрих Гаусс Время жизни 30.04.1777 - 23.02.1855 Научная сфера – математика, физика, астрономия Андрей Андреевич
- 4. Постановка задачи: Имеем случайную выборку наблюдений за поведением экономического объекта объемом n Выборка наблюдений за переменными
- 5. Сформируем вектора и матрицу коэффициентов на основе системы (7.2) Y – вектор выборочных значений эндогенной переменной
- 6. По данным выборки найти: Ã, Cov(ÃÃ), σu, σ(ỹ(z)) Теорема (Гаусса – Маркова) Если матрица Х неколлинеарна
- 7. Тогда наилучшей линейной процедурой оценки параметров модели (7.1) является: (7.3) которая удовлетворяет методу наименьших квадратов При
- 8. Доказательство Воспользуемся методом наименьших квадратов где (7.4) (7.5) Подставив (7.5) в (7.4) получим (7.6)
- 9. Для получения необходимого условия экстремума дифференцируем (7.6) по вектору параметров Откуда система нормальных уравнений для определения
- 10. Докажем несмещенность оценок (7.3) Несмещенность оценки (7.3) доказана Вычислим ковариационную матрицу оценок (7.3) В результате получено
- 11. Пример 1. Пусть имеем выборку из n наблюдений за случайной величиной Y Найти наилучшие оценки среднего
- 12. Решение 1. Вычисляем (XTX)-1 2. Вычисляем (XTY) 3. Вычисляем оценку параметра а0 4. Находим дисперсию среднего
- 13. Пример 2. Уравнение парной регрессии Построить модель типа Y=a0+a1x +u, по данным вы-борки наблюдений за переменными
- 14. 2. Вычисляем XTY 3. Вычисляем оценку вектора параметров а
- 15. Вычислим дисперсии (ковариационную матрицу) параметров модели Следовательно:
- 16. Расчет дисперсии прогнозирования Прогноз осуществляется в точке Z={1,z}Т
- 17. Процедура «ЛИНЕЙН» в приложении EXCEL Алгоритм использования процедуры: Подготовка таблицы исходных данных 2. Вызов процедуры «ЛИНЕЙН»
- 19. Скачать презентацию
















 Совершенствование работы автотранспортного предприятия ОАО Транссервис
Совершенствование работы автотранспортного предприятия ОАО Транссервис Импорт и экспорт Южной Кореи и стран лидеров (1970-2013 г.г.)
Импорт и экспорт Южной Кореи и стран лидеров (1970-2013 г.г.) Экономическое развитие России в XVII в
Экономическое развитие России в XVII в Российские новости в экономике
Российские новости в экономике Спрос и предложение
Спрос и предложение Мировая экономика в ХІХ веке
Мировая экономика в ХІХ веке Собственность. Рынок
Собственность. Рынок Ринок здорового хліба на Дніпропетровщині
Ринок здорового хліба на Дніпропетровщині Принципы разработки и реализации региональной экономической политики. Воспроизводство региональной экономики
Принципы разработки и реализации региональной экономической политики. Воспроизводство региональной экономики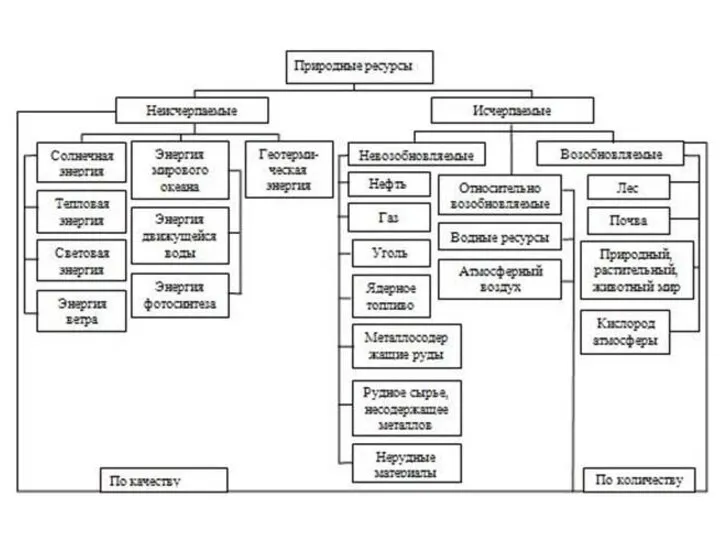 Нефтяной запас России
Нефтяной запас России Международная интеграция как объективное явление общественной жизни
Международная интеграция как объективное явление общественной жизни Спрос на потребительском рынке
Спрос на потребительском рынке Рынок как форма
Рынок как форма Инвестиционный проект предприятия автосервиса, созданный в программе Project Expert
Инвестиционный проект предприятия автосервиса, созданный в программе Project Expert Рынок. Структура рыночной экономики
Рынок. Структура рыночной экономики Пути совершенствования управления туристическим предприятием (на примере ООО Полярис, туристическое агентство Нуай Вояж)
Пути совершенствования управления туристическим предприятием (на примере ООО Полярис, туристическое агентство Нуай Вояж) Занятость и безработица
Занятость и безработица Введение в экономику
Введение в экономику Бюджетные ограничения (не все)
Бюджетные ограничения (не все) Життєвий шлях економiста Пола Ентонi Самуельсона
Життєвий шлях економiста Пола Ентонi Самуельсона Рынок труда. Безработица
Рынок труда. Безработица Макроэкономика: предмет, метод, основные понятия, показатели
Макроэкономика: предмет, метод, основные понятия, показатели Структура мировой экономики
Структура мировой экономики Нормативно-правове забезпечення облікового процесу та облікова політика підприємства (Лекція №2)
Нормативно-правове забезпечення облікового процесу та облікова політика підприємства (Лекція №2) Национальный человеческий капитал в экономическом пространстве 2030
Национальный человеческий капитал в экономическом пространстве 2030 Экономические системы
Экономические системы Совокупное предложение и спрос. Тема 2
Совокупное предложение и спрос. Тема 2 Удосконалення відносин власності у перехідній економіці
Удосконалення відносин власності у перехідній економіці