Поведение потребителя

Полезность семи конфет равна 40, а полезность восьми конфет равна 44. определите предельную полезность седьмой, восьмой и девятой конфеты

Первое яблоко доставляет Ивану удовлетворение, равное 8. Каждое следующее яблоко доставляет добавочное удовлетворение, на 2 меньше предыдущего. Начиная с какого яблока суммарное удовлетворение от потребления яблок будет уменьшаться?

Равновесный объем продуктов состоит из нескольких стаканов молока и нескольких кусков хлеба. Если в него добавить один стакан молока, то полезность набора увеличится на 12 единциц, а если добавить один кусок хлеба, то на 8 единиц. Цена стакана молока равна 9 руб. Найдите цену куска хлеба

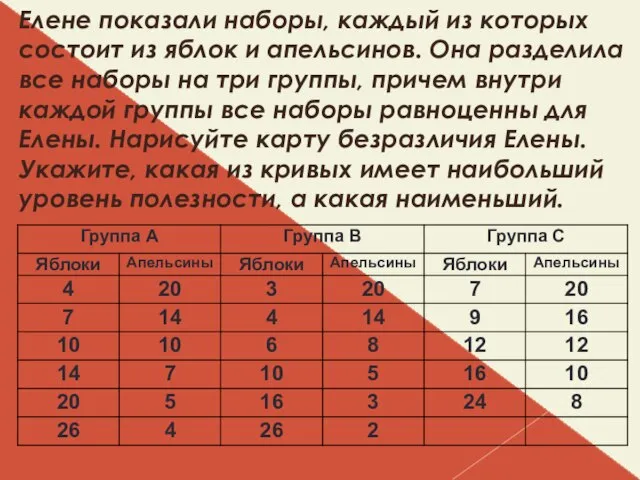
Елене показали наборы, каждый из которых состоит из яблок и апельсинов. Она разделила все наборы на три группы, причем внутри каждой группы все наборы равноценны для Елены. Нарисуйте карту безразличия Елены. Укажите, какая из кривых имеет наибольший уровень полезности, а какая наименьший.

Доход 200 руб. в неделю индивид тратит на покупку двух товаров по ценам Рх = 5 руб. и Ру = 10 руб. Нарисуйте бюджетную линию. Как изменится бюджетная линия при росте доходов до 240 руб.? Как пройдет бюджетная линия при доходе 200 и ценах Рх = 2,5 руб. и Ру = 4 руб.?

Бюджетное ограничение задано формулой 8х+6у=20. Найдите максимально возможный объем потребления продукта Х.

Студент еженедельно получает от родителей 800 рублей на карманные расходы. Начертите бюджетную линию студента для каждой из ситуаций, обозначив продукты питания по оси ординат, а развлечения – по оси абсцисс:
1) цена продуктов питания Рп = 20 рублей за единицу; цена развлечений Рр = 20 рублей за единицу; 2) Рп = 20 рублей за единицу; Рр = 40 рублей за единицу; 3) Рп = 40 рублей за единицу; Рр = 20 рублей за единицу; 4) Рп = 16 рублей за единицу; Рр = 16 рублей за единицу; 5) Рп = 20 рублей за единицу; Рр = 20 рублей за единицу, но доходы студента увеличиваются до 1000 рублей в неделю. Прокомментируйте бюджетные линии 4) и 5) и сравните их с бюджетной линией 1).

Индивид тратит весь доход либо на 8 единиц блага Х и 18 единиц блага У, либо на 12 единиц блага Х и 10 единиц У. Сколько единиц У сможет он купить, если вообще откажется от блага Х?

Иван обычно на свой доход покупал 300 единиц товара Х и 150 единиц товара У при ценах Рх = 6 и Ру = 12. Если цены изменятся до уровня Рх = 15 и Ру =24, то на сколько должен возрасти доход, чтобы он мог позволить себе тот же набор?

У всех покупателей на рынке стамесок наблюдается одинаковая функция индивидуального спроса Q = 8 – 0,5P. Определите функцию рыночного спроса, если покупателей на рынке 20 человек.

Петр покупает 30 роз в месяц по цене, меньшей 40 руб., и не покупает вовсе при больших ценах. Иван покупает 40 роз в месяц при цене, меньшей 30 руб., и не покупает вовсе при больших ценах. Постройте график суммарного спроса на розы.

Функция спроса Ивана Q = 6 – 3P, функция спроса Марии Q = 4 – 0,5P. Постройте кривую суммарного спроса.

Индивидуальный спрос трех покупателей: Алексея, Виктора и Сергея на шурупы задан следующими функциями:
QА = 24 – 6Р; QВ = 32 – 8Р;
QС = 44 – 11 Р.
Определите рыночный спрос трех покупателей и представьте его графически.

Известны коэффициенты эластичности спроса на товар Х: по цене самого товара Ех = – 2, по цене товара-конкурента Еху =+1,5, по доходу ЕI = +2. Как изменится в процентном отношении спрос на товар при 1) увеличении цены самого товара на 5%, 2) уменьшении цены товара-конкурента на 6%, 3) увеличении дохода потребителя на 3%?

При увеличении цены масла на 2% спрос на него сократился на 3%, а спрос на финское масло увеличился на 2,5%. Найдите эластичность спроса на масло и перекрестную эластичность спроса на маргарин.

В результате повышения цены с 5 до 6 рублей объем спроса сократился с 9 до 7 млн. штук в год. Определите коэффициент прямой эластичности.