Содержание
- 2. Ключевые вопросы 1. Как измерить риск? 2. Как соотносится риск с ожидаемой доходностью?
- 3. Риск вероятность неблагоприятного исхода; вероятность отклонения фактического результата от ожидаемого; возможная потеря, вызванная наступлением случайных неблагоприятных
- 4. Финансовый риск – увеличение неуверенности в достижении поставленной цели в связи с привлечением заемных средств. Случайная
- 5. Одними из основных показателей риска являются среднеквадратичное отклонение, коэффициент вариации относительное недостижение цели.
- 6. Изучение поведения интересующей нас случайной величины А можно начать с составления на основе имеющейся информации вероятностного
- 7. Среднее квадратическое отклонение 1.При одинаковой ожидаемой доходности выбираем проект с наименьшим СКО. 2.При равных значениях СКО
- 8. Коэффициент вариации Мера риска не единицу доходности
- 9. Если нашей целью является достижение случайной величиной А значения а*, то есть то математическое ожидание абсолютного
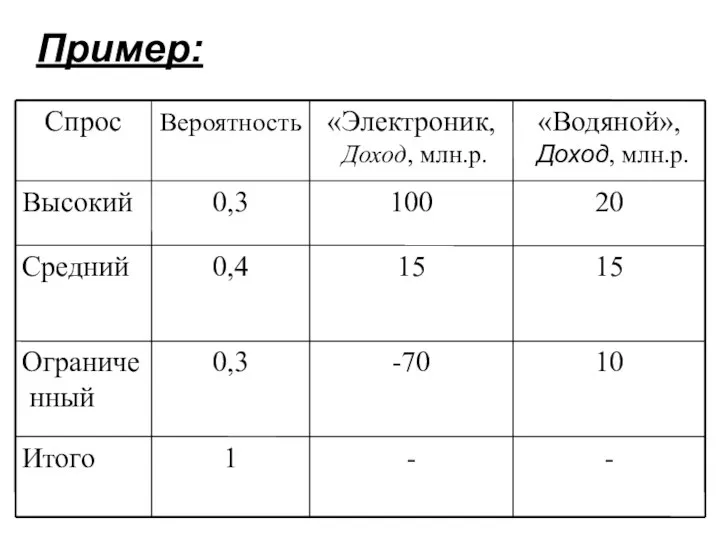
- 10. Пример:
- 11. Ожидаемая доходность проекта (EP) EP «Электроник» = 0,3*100+0,4*15+0,3*(-70) = 15 EP «Водяной» = 0,3*20+0,4*15+0,3*10 = 15
- 12. Среднее квадратическое отклонение доходности «Электроник» σ = 65,84 млн. р. «Водяной» σ = 3,87 млн. р.
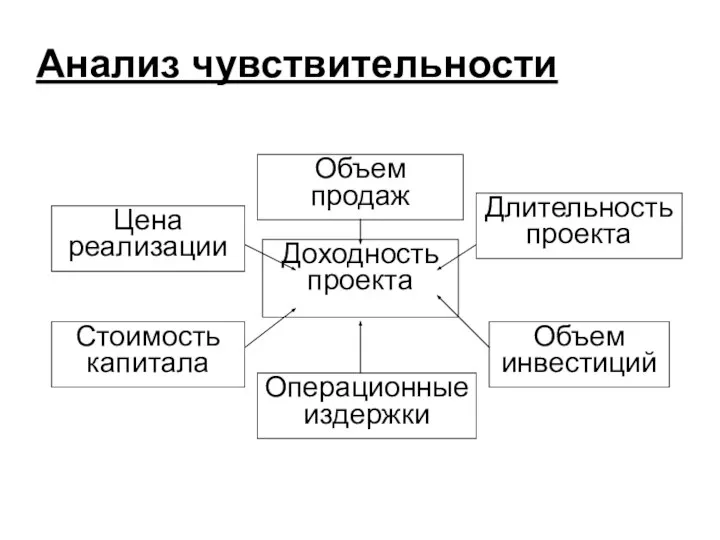
- 13. Анализ чувствительности Насколько доходность проекта может меняться в ответ на изменение одного из параметров что, если
- 14. Анализ чувствительности Доходность проекта Объем инвестиций Стоимость капитала Операционные издержки Цена реализации Объем продаж Длительность проекта
- 15. Анализ чувствительности Определение «запаса прочности» по каждому параметру проекта Анализ сценариев Оптимистический; Пессимистический; Наиболее реалистичный.
- 16. МОДЕЛЬ ХАУСТОНА позволяет определить эффективность страхования финансовых рисков организации. Это сравнительная оценка стоимости организации на конец
- 17. Стоимость активов организации на конец страхового периода при передаче финансового риска страховщику Стоимость активов организации на
- 18. Задача: Стоимость активов предприятия на начало страхового периода 200 000 руб. Сумма страховой премии составляет 12
- 19. Стоимость активов организации на конец страхового периода при передаче финансового риска страховщику Стоимость активов организации на
- 21. Скачать презентацию















 Наклонная линия. Правила построения
Наклонная линия. Правила построения Национальные интересы РФ
Национальные интересы РФ Теория организации как наука
Теория организации как наука Национальное богатство
Национальное богатство Обмен, торговля, реклама
Обмен, торговля, реклама Дисциплинарные картины мира. Экономика, как наука
Дисциплинарные картины мира. Экономика, как наука Валюта иена
Валюта иена Экономика предприятия
Экономика предприятия Статистика системы национальных счетов. Тема 1. Понятие системы национальных счетов, категории и группировки
Статистика системы национальных счетов. Тема 1. Понятие системы национальных счетов, категории и группировки Экономика Челябинской области
Экономика Челябинской области Производство - основа экономики
Производство - основа экономики Закон самосохранения организации
Закон самосохранения организации Факторы производства, разделение труда, специализация и обмен
Факторы производства, разделение труда, специализация и обмен Организационные формы предприятий
Организационные формы предприятий Нобелевские лауреаты области экономических исследований и современные направления экономической науки
Нобелевские лауреаты области экономических исследований и современные направления экономической науки Сбережения и инвестиции
Сбережения и инвестиции Διδακτική Ενότητα Γ: Πιθανότητες
Διδακτική Ενότητα Γ: Πιθανότητες Структура смертности населения Павловского района
Структура смертности населения Павловского района Экономическая теория. Для студентов заочной формы обучения
Экономическая теория. Для студентов заочной формы обучения Сетевая экономика РФ и США
Сетевая экономика РФ и США Процесс производства и его факторы. Практическое занятие 2
Процесс производства и его факторы. Практическое занятие 2 Мировая экономика и современные тенденции ее развития
Мировая экономика и современные тенденции ее развития Всемирный экономический форум
Всемирный экономический форум Реформы по улучшению позиции Казахстана по индикаторам рейтинга Doing business
Реформы по улучшению позиции Казахстана по индикаторам рейтинга Doing business Предприятие в системе общественного разделения труда. Типизация предприятий. (Тема 2)
Предприятие в системе общественного разделения труда. Типизация предприятий. (Тема 2) Макроэкономические показатели. Решение задач
Макроэкономические показатели. Решение задач Экономика Тихого Океана
Экономика Тихого Океана Логистика управления запасами
Логистика управления запасами