Содержание
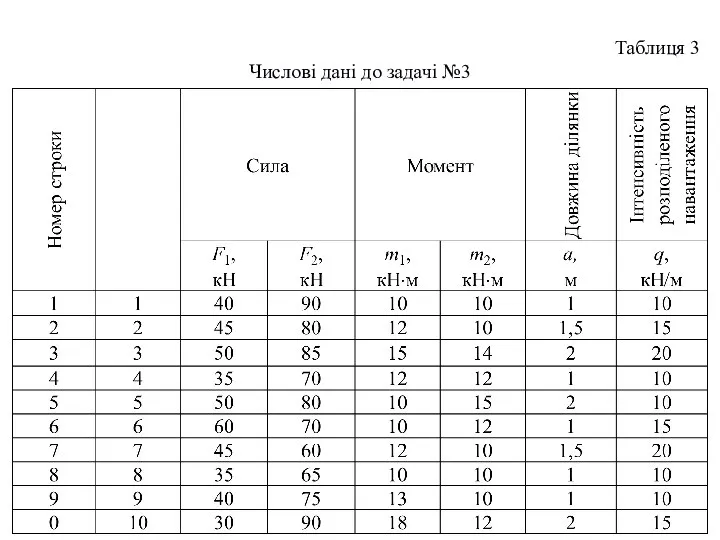
- 2. Таблиця 3 Числові дані до задачі №3
- 3. Рис.6 Розрахункові схеми балок до задачі № 3.
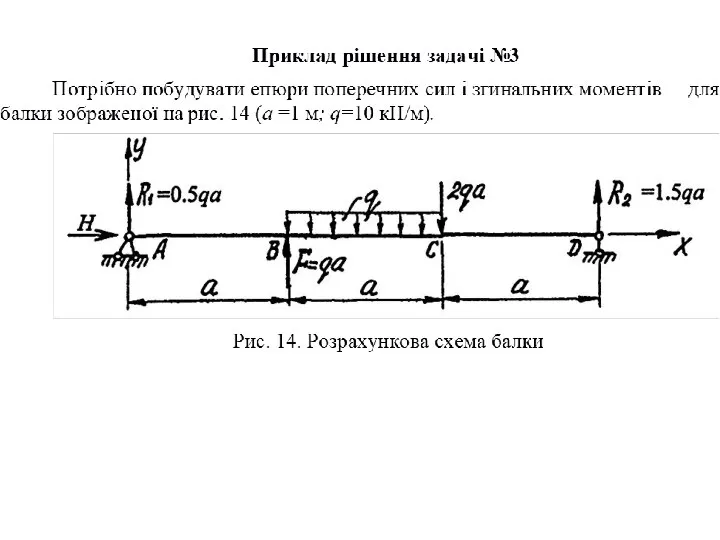
- 4. Методичні вказівки до рішення задачі № 3 Основні теоретичні відомості та розрахункові формули При згинанні в
- 5. Рис. 7. Правило знаків для поперечної сили Рис. 8. Правило знаків для згинального моменту Розв’язок задач,
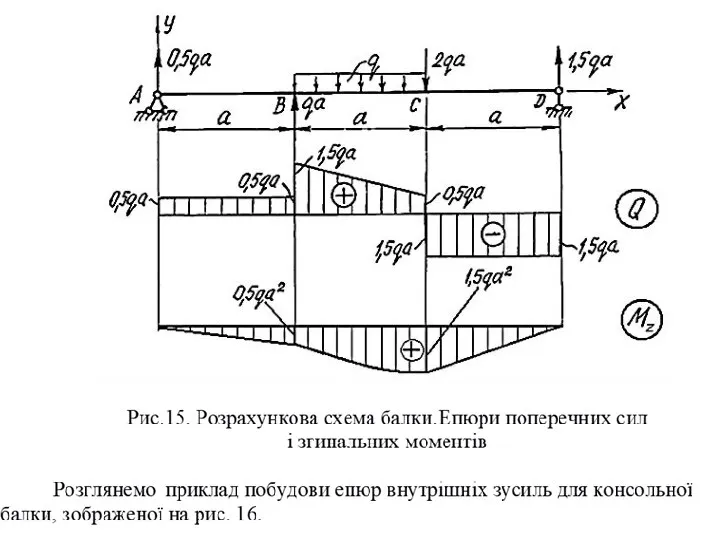
- 6. Залежності (3.1) дозволяють встановити такі характерні особливості епюр поперечних сил і згинальних моментів: На ділянках, де
- 7. Рис. 9 Рис. 10
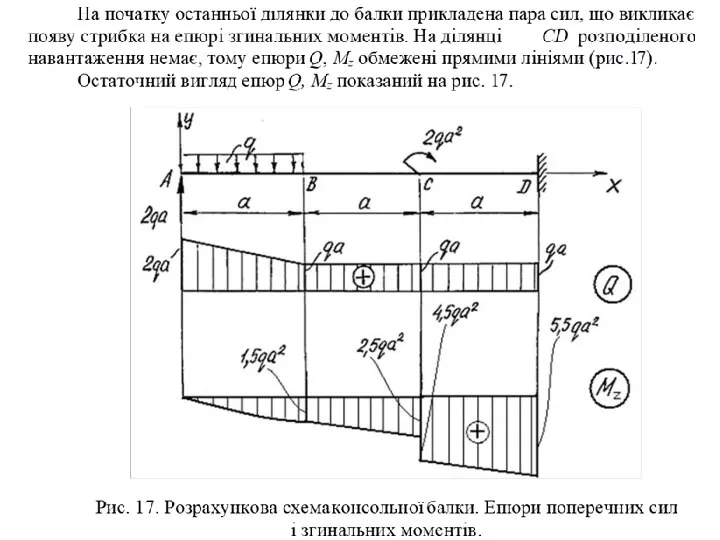
- 8. У перерізах, де до балки прикладені зосереджені сили, на епюрі Q будуть скачки на величину прикладених
- 9. Якщо на кінці консолі або в кінцевій опорі до балки прикладений зосереджений момент, то в цьому
- 22. Скачать презентацию
Слайд 3Рис.6 Розрахункові схеми балок до задачі № 3.
Рис.6 Розрахункові схеми балок до задачі № 3.

Слайд 4Методичні вказівки до рішення задачі № 3
Основні теоретичні відомості та розрахункові формули
При
Методичні вказівки до рішення задачі № 3
Основні теоретичні відомості та розрахункові формули
При

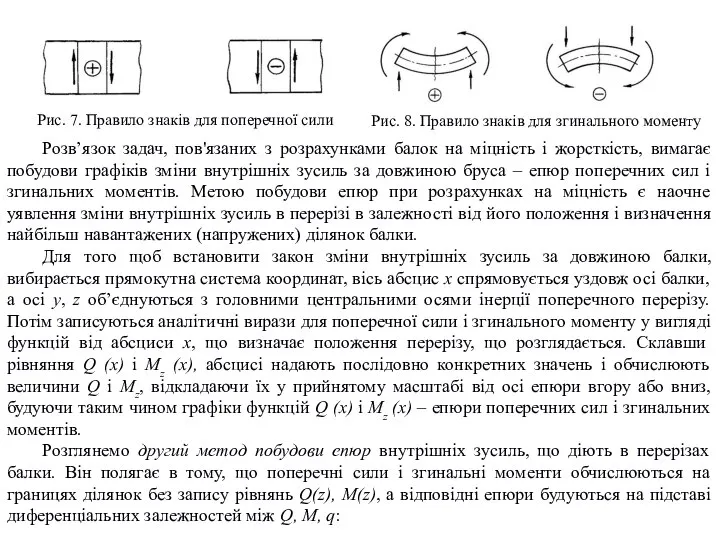
Поперечною силою в перерізі називається внутрішнє зусилля, чисельно рівне алгебраїчній сумі проекцій всіх сил, що діють на балку з одного боку від перерізу, на нормаль до осі балки. Поперечна сила вважається додатною, якщо вона прагне обертати нескінченно малий елемент балки за ходом годинникової стрілки. Зворотний напрямок обертання відповідає від’ємній поперечної силі (рис. 7).
Згинальним моментом в перерізі балки називається внутрішнє зусилля, чисельно рівне алгебраїчній сумі моментів зовнішніх сил, що діють на балку з одного боку від перерізу, відносно її центра ваги. Згинальний момент додатний, якщо під його впливом балка згинається опуклістю вниз; при вигині опуклістю вгору згинальний момент вважається від’ємним (рис. 8). Епюра згинальних моментів будується з боку розтягненого волокна балки, яке знаходиться з випуклої частини балки. Додатні значення згинального моменту відкладаються вниз від осі епюри, від’ємні – вгору.
Слайд 5Рис. 7. Правило знаків для поперечної сили
Рис. 8. Правило знаків для згинального
Рис. 7. Правило знаків для поперечної сили
Рис. 8. Правило знаків для згинального
Розв’язок задач, пов'язаних з розрахунками балок на міцність і жорсткість, вимагає побудови графіків зміни внутрішніх зусиль за довжиною бруса – епюр поперечних сил і згинальних моментів. Метою побудови епюр при розрахунках на міцність є наочне уявлення зміни внутрішніх зусиль в перерізі в залежності від його положення і визначення найбільш навантажених (напружених) ділянок балки.
Для того щоб встановити закон зміни внутрішніх зусиль за довжиною балки, вибирається прямокутна система координат, вісь абсцис x спрямовується уздовж осі балки, а осі y, z об’єднуються з головними центральними осями інерції поперечного перерізу. Потім записуються аналітичні вирази для поперечної сили і згинального моменту у вигляді функцій від абсциси x, що визначає положення перерізу, що розглядається. Склавши рівняння Q (x) і Mz (x), абсцисі надають послідовно конкретних значень і обчислюють величини Q і Mz, відкладаючи їх у прийнятому масштабі від осі епюри вгору або вниз, будуючи таким чином графіки функцій Q (x) і Mz (x) – епюри поперечних сил і згинальних моментів.
Розглянемо другий метод побудови епюр внутрішніх зусиль, що діють в перерізах балки. Він полягає в тому, що поперечні сили і згинальні моменти обчислюються на границях ділянок без запису рівнянь Q(z), M(z), а відповідні епюри будуються на підставі диференціальних залежностей між Q, M, q:
Слайд 6Залежності (3.1) дозволяють встановити такі характерні особливості епюр поперечних сил і згинальних
Залежності (3.1) дозволяють встановити такі характерні особливості епюр поперечних сил і згинальних

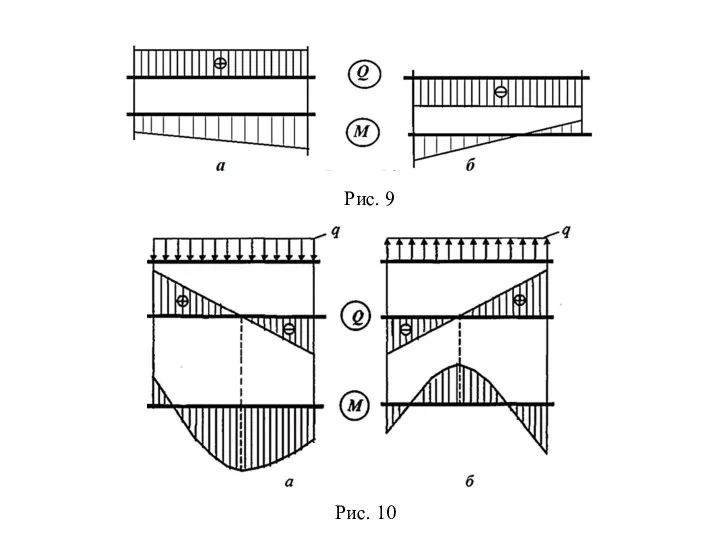
На ділянках, де немає розподіленого навантаження, епюра Q обмежена прямими, паралельними осі балки, а епюра M – похилими прямими (рис. 9, а – Q>0 і рис. 9, б – Q < 0).
На ділянках, де прикладено рівномірно розподілене навантаження інтенсивністю q, епюра Q обмежена похилими прямими, а епюра M – квадратними параболами, опуклість яких спрямована за вектором рівномірно розподіленого навантаження (рис.10, а і б).
На ділянках, де Q > 0, згинальний момент зростає (рис. 10, а); якщо Q <0 – згинальний момент спадає (рис. 10, б).
Слайд 7Рис. 9
Рис. 10
Рис. 9
Рис. 10
Слайд 8У перерізах, де до балки прикладені зосереджені сили, на епюрі Q будуть
У перерізах, де до балки прикладені зосереджені сили, на епюрі Q будуть
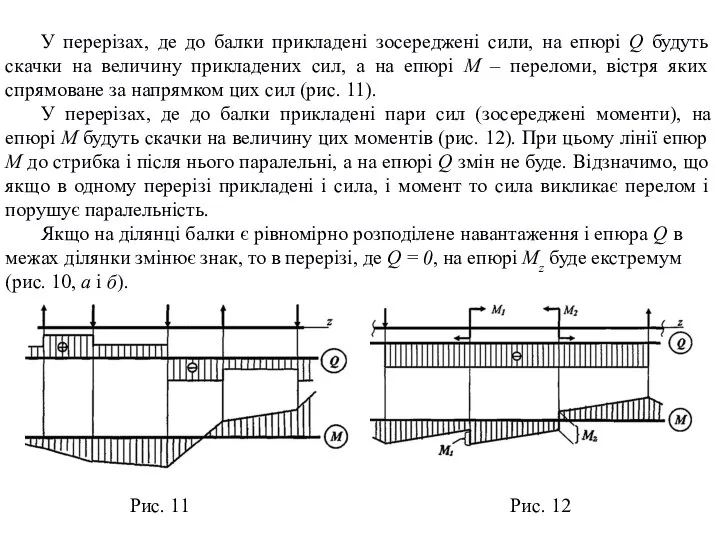
У перерізах, де до балки прикладені пари сил (зосереджені моменти), на епюрі M будуть скачки на величину цих моментів (рис. 12). При цьому лінії епюр М до стрибка і після нього паралельні, а на епюрі Q змін не буде. Відзначимо, що якщо в одному перерізі прикладені і сила, і момент то сила викликає перелом і порушує паралельність.
Якщо на ділянці балки є рівномірно розподілене навантаження і епюра Q в межах ділянки змінює знак, то в перерізі, де Q = 0, на епюрі Mz буде екстремум (рис. 10, а і б).
Рис. 11
Рис. 12
Слайд 9Якщо на кінці консолі або в кінцевій опорі до балки прикладений зосереджений
Якщо на кінці консолі або в кінцевій опорі до балки прикладений зосереджений
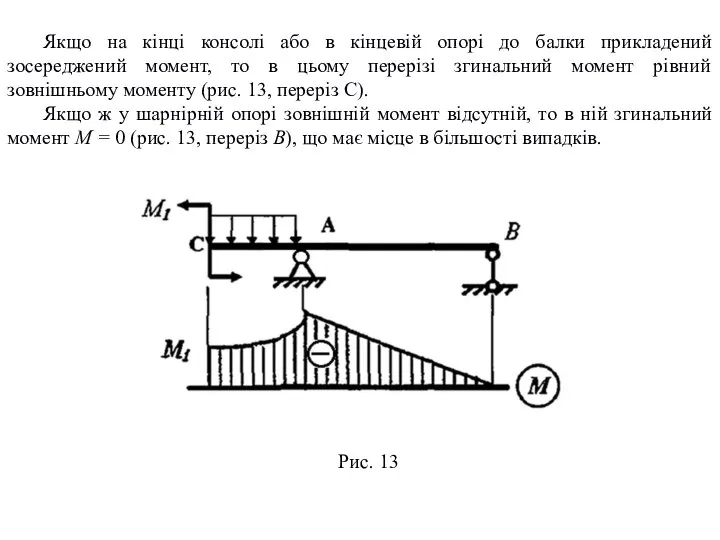
Якщо ж у шарнірній опорі зовнішній момент відсутній, то в ній згинальний момент М = 0 (рис. 13, переріз В), що має місце в більшості випадків.
Рис. 13







 Открытая лаборатория. Физика - наука о природе
Открытая лаборатория. Физика - наука о природе Относительность механического движения
Относительность механического движения Олимпийские игры в Афинах 2004 год
Олимпийские игры в Афинах 2004 год Исследование процессов неупругих столкновений
Исследование процессов неупругих столкновений Эпюры
Эпюры Скорость витания
Скорость витания Приборы и методы экспериментальной физики
Приборы и методы экспериментальной физики Вопросы транспорта и логистики на шельфе
Вопросы транспорта и логистики на шельфе Переменный ток. Решение задач
Переменный ток. Решение задач Наука физика
Наука физика Презентация на тему Звук
Презентация на тему Звук  Температура и тепловое движение Тепловые явления-явления, связанные с изменением
Температура и тепловое движение Тепловые явления-явления, связанные с изменением Электрическое поле
Электрическое поле Дифракция света. Лекции 14-15
Дифракция света. Лекции 14-15 Современные методы научных исследований и основы подготовки диссертаций
Современные методы научных исследований и основы подготовки диссертаций Измерительные трансформаторы напряжения
Измерительные трансформаторы напряжения Намагничивание вещества. Вектор намагничивания J
Намагничивание вещества. Вектор намагничивания J Электростатика. 8 класс
Электростатика. 8 класс Тестирование Демо РТ1. (Задания)
Тестирование Демо РТ1. (Задания) Электроизмерительные приборы
Электроизмерительные приборы Работа и мощность электрического тока
Работа и мощность электрического тока Особенность расчета болтовых групповых соединений с зазором при поперечной нагрузке
Особенность расчета болтовых групповых соединений с зазором при поперечной нагрузке Safarov_Krasnov
Safarov_Krasnov Статистическая теория радиотехнических систем. Задача фильтрации. (Лекция 13)
Статистическая теория радиотехнических систем. Задача фильтрации. (Лекция 13) Работа с lego mindstorms ev3. Задание № 1: движение вперед и назад
Работа с lego mindstorms ev3. Задание № 1: движение вперед и назад Резьба. Элементы резьбы
Резьба. Элементы резьбы Действие жидкости и газа на погруженное в них тело
Действие жидкости и газа на погруженное в них тело Некогерентность рассеяния. (Тема 15)
Некогерентность рассеяния. (Тема 15)