Содержание
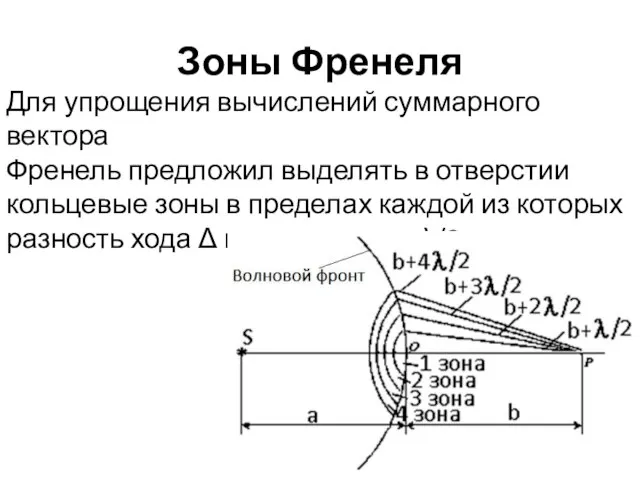
- 2. Зоны Френеля Для упрощения вычислений суммарного вектора Френель предложил выделять в отверстии кольцевые зоны в пределах
- 4. Пятиминутка. Сколько зон Френеля уместится в отверстии диаметром 0.5 мм, если расстояние от источника света до
- 5. Дифракционная картина от маленького отверстия представляет собой чередование светлых и темных колец. Освещенность центрального пятна опреде-лится
- 6. В результате при вычислении освещенности центральной точки дифракционной картины вместо спирали Френеля мы получим картину, показанную
- 7. В результате мы получаем плос-кую и тонкую линзу, очень по-лезную во мно-гих практичес-ких случаях. Задача: Фазовая
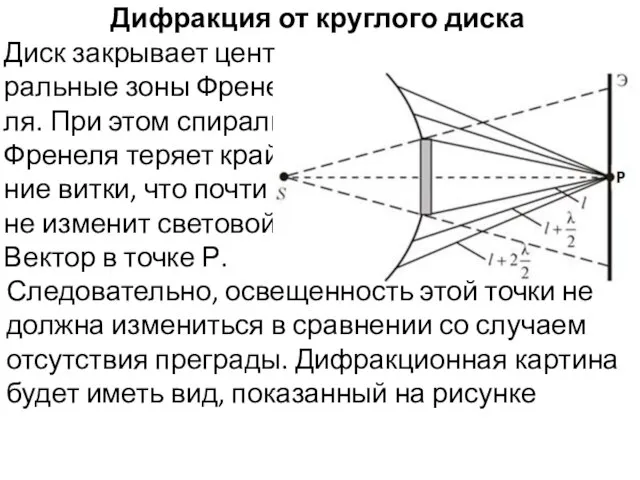
- 8. Дифракция от круглого диска Диск закрывает цент- ральные зоны Френе- ля. При этом спираль Френеля теряет
- 9. Светлое пятно в центре тени от диска называется пятном Пуассона. При опытах вместо диска обычно используют
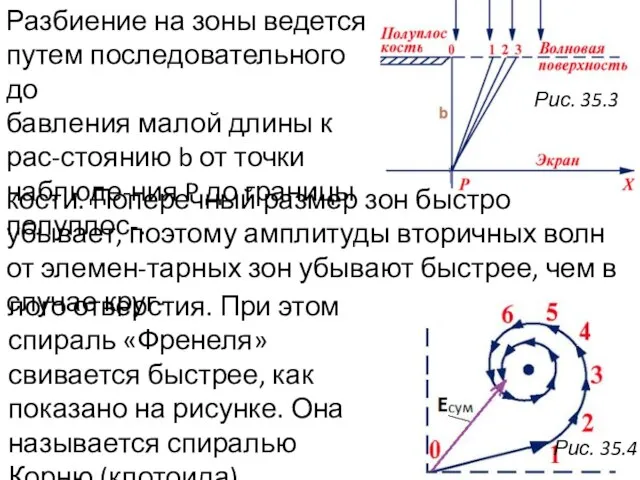
- 10. Разбиение на зоны ведется путем последовательного до бавления малой длины к рас-стоянию b от точки наблюде-ния
- 11. В таком виде спираль корню может использоваться для определения ос-вещенности в области геометричес-кой тени. Пусть точка
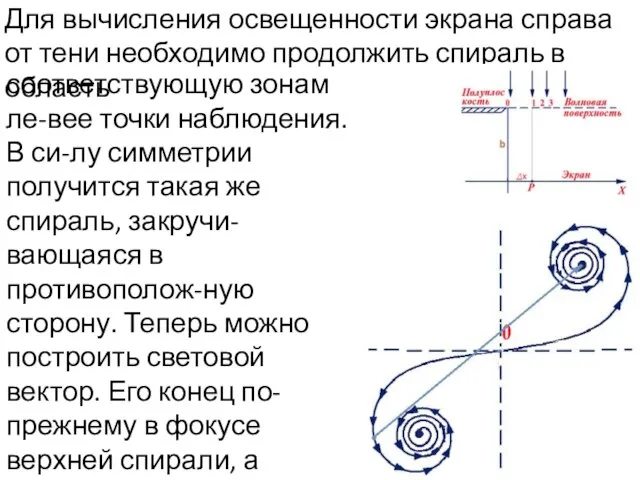
- 12. Для вычисления освещенности экрана справа от тени необходимо продолжить спираль в область соответствующую зонам ле-вее точки
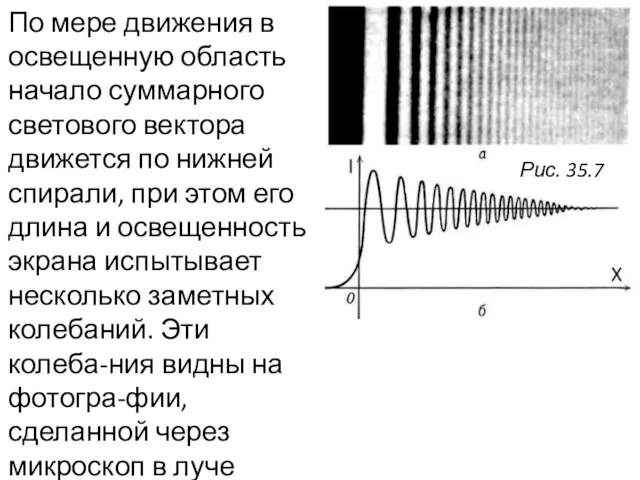
- 13. По мере движения в освещенную область начало суммарного светового вектора движется по нижней спирали, при этом
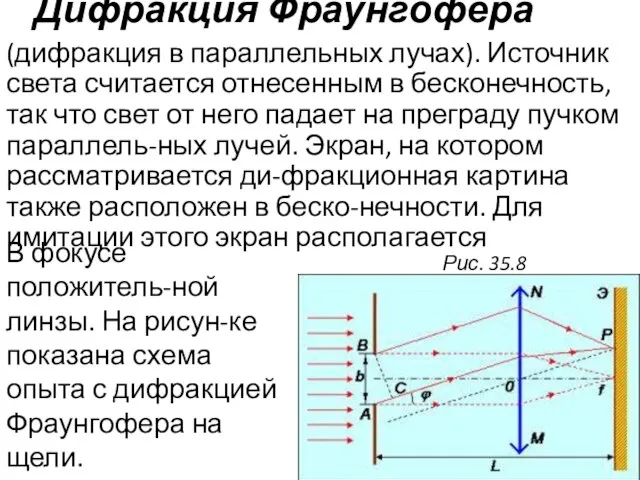
- 14. Дифракция Фраунгофера (дифракция в параллельных лучах). Источник света считается отнесенным в бесконечность, так что свет от
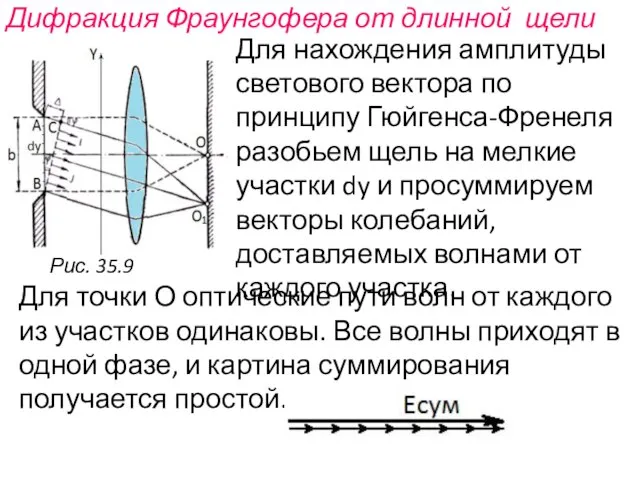
- 15. Дифракция Фраунгофера от длинной щели Для нахождения амплитуды светового вектора по принципу Гюйгенса-Френеля разобьем щель на
- 16. суммируемых векторов коле-баний. На рис. Показано определение амплитуды светового вектора для разных направлений. Рис. 35.11
- 17. При φ=0 дуга окружности разворачивается в прямую линию, что соответствует центральному максимуму дифракционной картины. При увеличении
- 18. Рис. 35.12
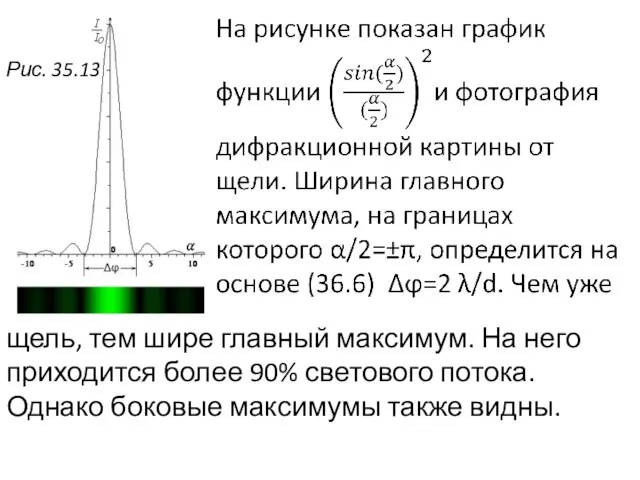
- 20. щель, тем шире главный максимум. На него приходится более 90% светового потока. Однако боковые максимумы также
- 21. Дифракция на проволоке. Принцип Бабине. Для нахождения дифракционной картины от проволоки толщиной d проведем следующие рассуждения.
- 22. Обозначим распределение поля на экране в слу-чае дифракции на щели Uщ(φ), а на проволоке - Uп
- 23. Таким образом, сумма распределений полей от дополнительных объектов равна полю, наблю-даемому на экране при отсутствии препятствия.
- 24. Дифракционная решетка. Дифракционная решётка - оптический прибор, предназначенный для анализа спектрального сос-тава оптического излучения. Дифракционная ре-шётка
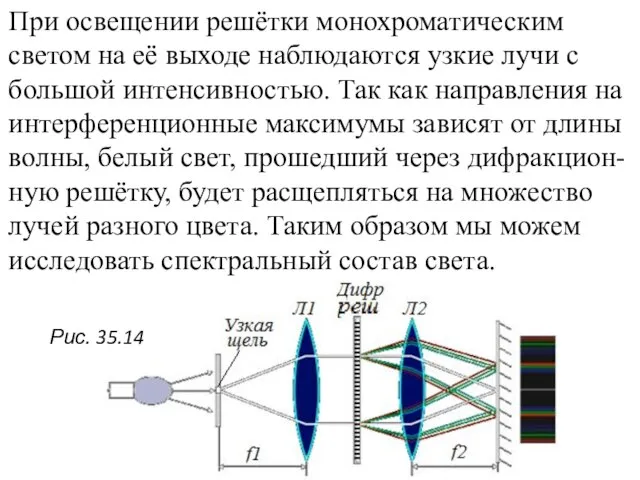
- 25. При освещении решётки монохроматическим светом на её выходе наблюдаются узкие лучи с большой интенсивностью. Так как
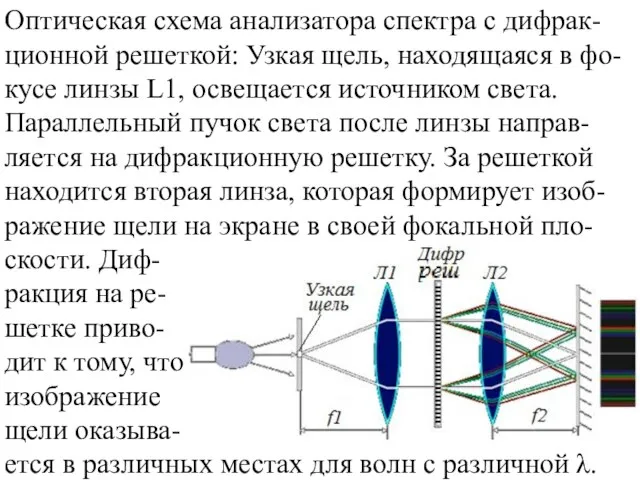
- 26. Оптическая схема анализатора спектра с дифрак-ционной решеткой: Узкая щель, находящаяся в фо-кусе линзы L1, освещается источником
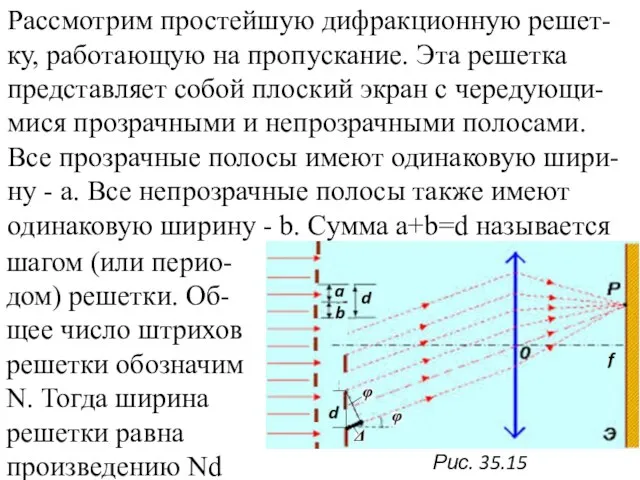
- 27. Рассмотрим простейшую дифракционную решет-ку, работающую на пропускание. Эта решетка представляет собой плоский экран с чередующи-мися прозрачными
- 28. Главный дифракционный максимум образуется при условии, что волны от соседних штрихов ре-шетки приходят в точку наблюдения
- 29. Оценим амплитуду дифрагировавшей волны и ее зависимость от угла дифракции φ. Разность фаз между волнами от
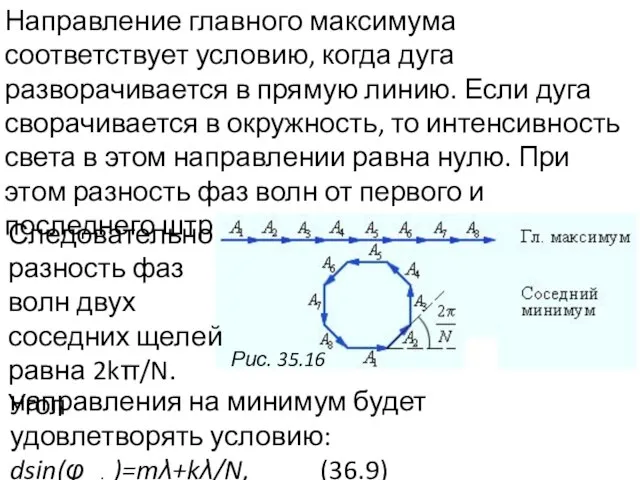
- 30. Направление главного максимума соответствует условию, когда дуга разворачивается в прямую линию. Если дуга сворачивается в окружность,
- 31. Сравним условия дифракционного максимума (35.7) и дифракционного минимума (36.9) dsin(φmax)=mλ, – условие максимума (36.8) dsin(φmin)=mλ+kλ/N, –
- 32. Определим угловую ширину какого-либо главного максимума как разность углов φmax- φmin при k=1, т.е. угловое расстояние
- 34. Скачать презентацию



















 Метрология. Случайные погрешности: статистические методы оценивания
Метрология. Случайные погрешности: статистические методы оценивания Единицы работы электрического тока, применяемые на практике
Единицы работы электрического тока, применяемые на практике Оптические явления
Оптические явления МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ
МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ  Презентация на тему Электрическая цепь
Презентация на тему Электрическая цепь  Адиабатическое приближение
Адиабатическое приближение Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7
Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7 Физика. Физические явления
Физика. Физические явления Динер Никита Физика Инерция
Динер Никита Физика Инерция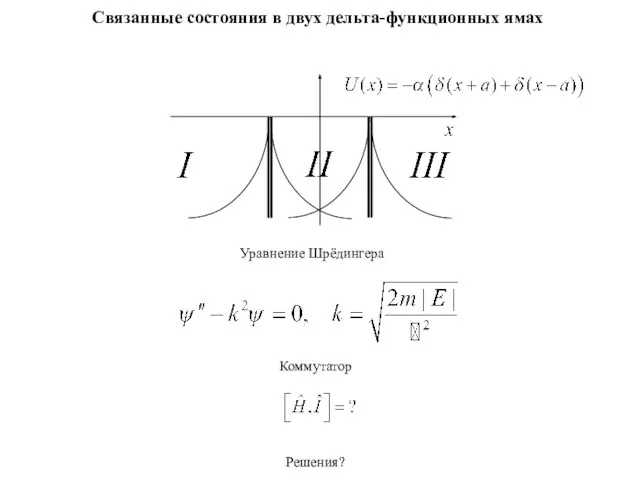 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Солнце, воздух и вода – наши лучшие друзья
Солнце, воздух и вода – наши лучшие друзья Револьверный станок
Револьверный станок Магнитное поле
Магнитное поле Внутренняя энергия. Работа в термодинамике. Количество теплоты
Внутренняя энергия. Работа в термодинамике. Количество теплоты Иллюзии и Физика. Вечная Борьба
Иллюзии и Физика. Вечная Борьба Теория пластин
Теория пластин Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля Сила трения
Сила трения Презентация на тему Кипение
Презентация на тему Кипение  Интерактивные лабораторные работы по физике
Интерактивные лабораторные работы по физике Нанотехнологии вокруг нас
Нанотехнологии вокруг нас Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила
Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила  Физика и В.О.В
Физика и В.О.В Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)
Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)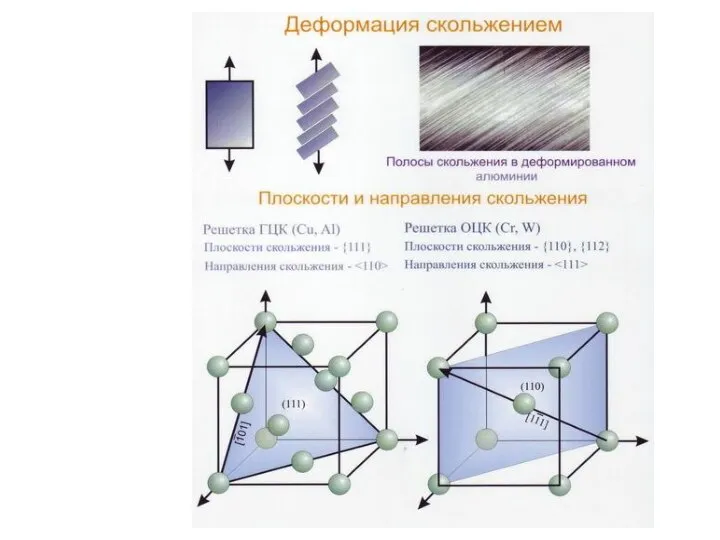 Пластическая деформация металлов
Пластическая деформация металлов ИК-спектроскопия
ИК-спектроскопия Техобслуживание
Техобслуживание Термодинамические системы и термодинамические параметры
Термодинамические системы и термодинамические параметры