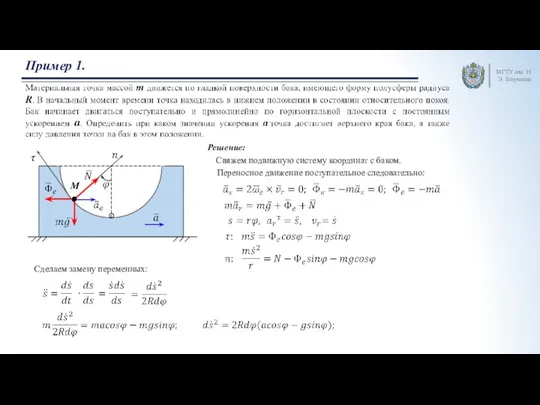
востоку.
Пусть тело падает на Землю с некоторой высоты H под действием силы тяжести.
Тогда ускорение Кориолиса
направлено по касательной к параллели на запад.
А сила инерции Кориолиса – по касательной к параллели на восток.
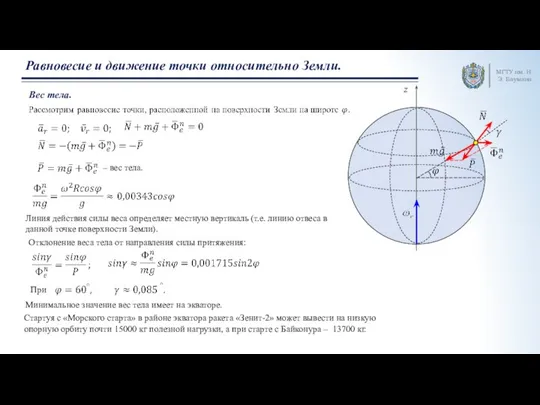
Движение вдоль параллели.
При движении точки вдоль параллели, сила инерции Кориолиса направлена вдоль одной линии с переносной силой инерции.
При движении на запад эти силы направлены в одну сторону, при движении на восток – в противоположные.
При движении точки по параллели изменяется только ее вес.





 Физическое явление. Оценка ответов учащихся
Физическое явление. Оценка ответов учащихся Коэффициент полезного действия механизма. Дома: §61 Повторить «золотое правило» механики. Познакомиться с понятием коэффициента полезного действия как основной характеристики рабочего механизма.
Коэффициент полезного действия механизма. Дома: §61 Повторить «золотое правило» механики. Познакомиться с понятием коэффициента полезного действия как основной характеристики рабочего механизма. Явление трения. Сила трения
Явление трения. Сила трения Закон всемирного тяготения
Закон всемирного тяготения Летняя практика
Летняя практика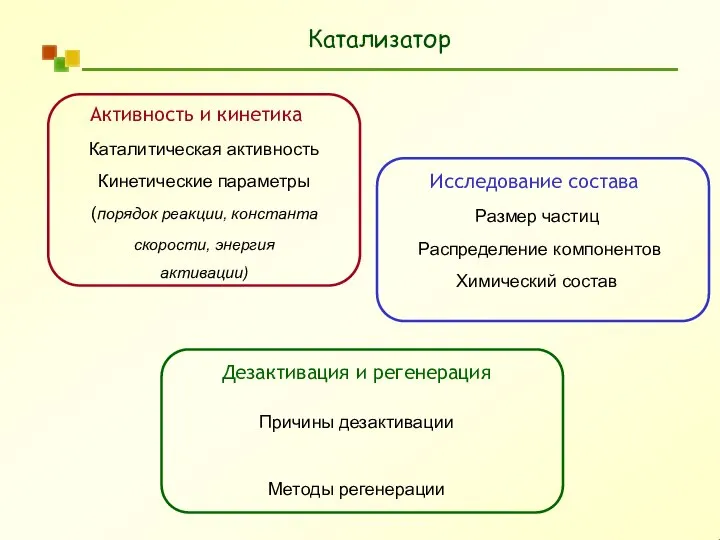 Катализатор. Анализ кинетических данных
Катализатор. Анализ кинетических данных История развития радио. Радиоквиз
История развития радио. Радиоквиз Расчет скорости, пути и времени механического движения
Расчет скорости, пути и времени механического движения Электромагнитные волны
Электромагнитные волны Гидротрансформатор
Гидротрансформатор Физика для одноклассников. 10 класс
Физика для одноклассников. 10 класс Откуда приходит электричество?
Откуда приходит электричество? Max.Industries. Технология термоядерного реактора
Max.Industries. Технология термоядерного реактора Исследование радиотехнической системы контроля положения нарушителя
Исследование радиотехнической системы контроля положения нарушителя Оптоволокно. Типы оптоволокон
Оптоволокно. Типы оптоволокон Термодинамика. Подготовка к контрольной работе
Термодинамика. Подготовка к контрольной работе Линейчатые оптические спектры. Поглощение и испускание света атомами
Линейчатые оптические спектры. Поглощение и испускание света атомами Гидравлика и ГП
Гидравлика и ГП Tvizi - Линейка электромобилей
Tvizi - Линейка электромобилей Шаровая машина для гоосования Александра Кондрашова
Шаровая машина для гоосования Александра Кондрашова Индукция магнитного поля (9 класс)
Индукция магнитного поля (9 класс) Кот Шрёдингера. Коллапс волновой функции. Введение в квантовую физику
Кот Шрёдингера. Коллапс волновой функции. Введение в квантовую физику Управление параметрами излучения мультиферроиковой структуры электрическим полем
Управление параметрами излучения мультиферроиковой структуры электрическим полем Механическое движение
Механическое движение Еволюція фізичної картини світу. Фізика і науково-технічний прогрес. Урок 98
Еволюція фізичної картини світу. Фізика і науково-технічний прогрес. Урок 98 Сложное движение точки
Сложное движение точки Основные понятия. Цепи постоянного тока
Основные понятия. Цепи постоянного тока Распределения Максвелла и Больцмана
Распределения Максвелла и Больцмана