Слайд 6Линейный закон распределения скоростей в потоке
Вязкость масла зависит от температуры и давления.
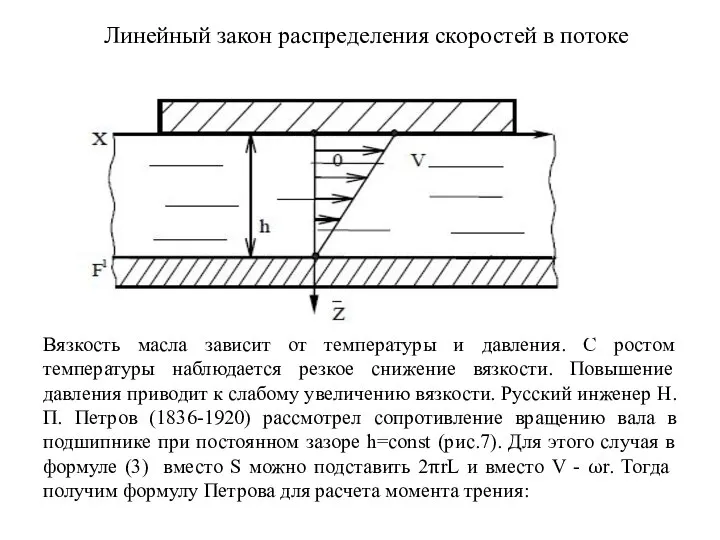
С ростом температуры наблюдается резкое снижение вязкости. Повышение давления приводит к слабому увеличению вязкости. Русский инженер Н.П. Петров (1836-1920) рассмотрел сопротивление вращению вала в подшипнике при постоянном зазоре h=const (рис.7). Для этого случая в формуле (3) вместо S можно подставить 2πrL и вместо V - ωr. Тогда получим формулу Петрова для расчета момента трения:
Слайд 7(4)
Коэффициент трения выразится:
(5)
Здесь L - длина подшипника; ω - угловая скорость

вала; h ˂˂ r. Из формулы видно, что момент трения увеличивается с ростом вязкости, угловой скорости, радиуса, длины подшипника и с уменьшением зазора. Наиболее сильно влияет радиус подшипника, он в третьей степени.
Слайд 8 Если постоянство зазора не поддерживать искусственным путем, то вал опустится под

действием силы тяжести. Зазор снизу начнет убывать. Здесь в действие включается гидродинамический эффект. Гидродинамический эффект заключается в том, что вал захватывает за счет смачивания масло и нагнетает его в сужающийся по направлению движения клиновой зазор. Внутри масляного клина возникает добавочное давление, эпюра которого показана на рисунке.
Вал всплывает при некоторой толщине
смазочного слоя, когда в результате
саморегулирования устанавливается
минимальный зазор нагруженной зоны
подшипника, соответствующий
действующей нагрузке N:
(6)
где k - коэффициент,
q=N/L - погонная нагрузка.
Слайд 9
Минимальной зазор возникает в сечении, смещенном на угол β. Для того

чтобы выразить подъемную силу масляного клина, силу вязкого трения и минимальную толщину зазора, необходимо решать уравнение Рейнольдса. Для жестких элементов пары трения, несжимаемой жидкости и стационарного течения это уравнение в интегральной форме имеет вид:
(7)
Здесь hо - толщина зазора в области максимального давления; h - текущая величина зазора. Решение уравнения Рейнольдса редко удается получить в аналитическом виде. Оно выполняется обычно численными методами.
Слайд 10Диаграмма Герси - Штрибека
Входящую в формулу (6) безразмерную величину λ= ηV/q
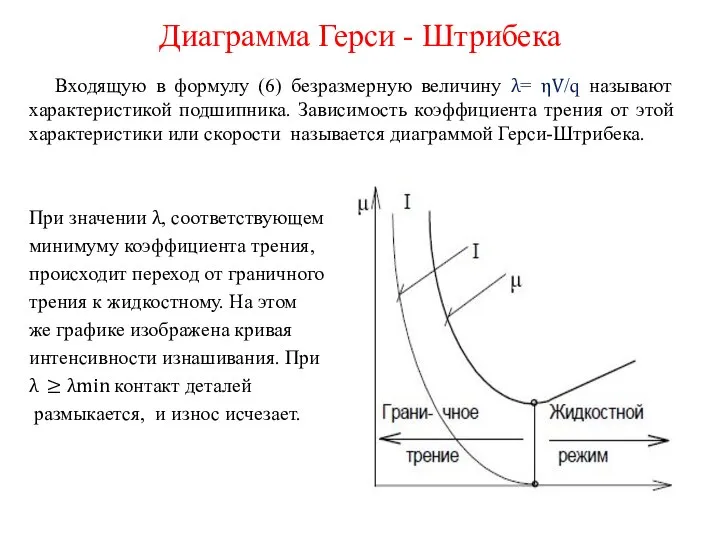
называют характеристикой подшипника. Зависимость коэффициента трения от этой характеристики или скорости называется диаграммой Герси-Штрибека.
При значении λ, соответствующем
минимуму коэффициента трения,
происходит переход от граничного
трения к жидкостному. На этом
же графике изображена кривая
интенсивности изнашивания. При
λ ≥ λmin контакт деталей
размыкается, и износ исчезает.
Слайд 11Эластогидродинамический эффект
Разновидностью гидродинамической является эластогидродинамическая смазка. Высокие давления в масляном клине

вызывают упругую деформацию контактирующих тел. В результате величина зазора между деталями возрастает. Особенно сильно этот эффект проявляется при трении тел, материал которых имеет низкий модуль упругости, например для резиновых колес автомобилей. На рис. показан эластогидродинамический эффект при качении колеса по жесткому
основанию. За счет эластогидродина-
мического эффекта смазка образует
прослойку между колесом и
основанием. Так происходит при
движении автомобиля по залитому
водой асфальту при скорости более
70 км/ч. Явление называют
глиссированием. Автомобиль
становится неуправляемым со всеми
вытекающими последствиями.











 Манометры
Манометры Элементы квантовой статистики
Элементы квантовой статистики Состав и характеристика атомного ядра. Лекция16
Состав и характеристика атомного ядра. Лекция16 Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо
Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо Магнитное поле
Магнитное поле Связь ДПФ и ДВПФ
Связь ДПФ и ДВПФ Кинематика. Материя. Виды движения
Кинематика. Материя. Виды движения Архимедова сила. Решение задач
Архимедова сила. Решение задач АМ БМ ОМ - математические модели сигналов. Тест
АМ БМ ОМ - математические модели сигналов. Тест Презентация на тему Сила трения. Трение в природе и технике
Презентация на тему Сила трения. Трение в природе и технике  Термодинамика. Лекция 6
Термодинамика. Лекция 6 Презентация на тему Гравитационные силы
Презентация на тему Гравитационные силы  ВКР: Ремонт двигателя внутреннего сгорания автомобиля УАЗ 3741
ВКР: Ремонт двигателя внутреннего сгорания автомобиля УАЗ 3741 Динамика и устойчивость сооружений
Динамика и устойчивость сооружений Вычислительные методы механики деформируемого тела
Вычислительные методы механики деформируемого тела Презентация на тему Равновесие тел
Презентация на тему Равновесие тел  Повторение. Физика атомного ядра
Повторение. Физика атомного ядра Электроионизационная технология
Электроионизационная технология Метод составления уравнений движения гибкого кольца
Метод составления уравнений движения гибкого кольца Работа и мощность электрического тока. Закон Джоуля-Ленца. КПД источника тока
Работа и мощность электрического тока. Закон Джоуля-Ленца. КПД источника тока Коллективные спасательные средства. Тема 2.3
Коллективные спасательные средства. Тема 2.3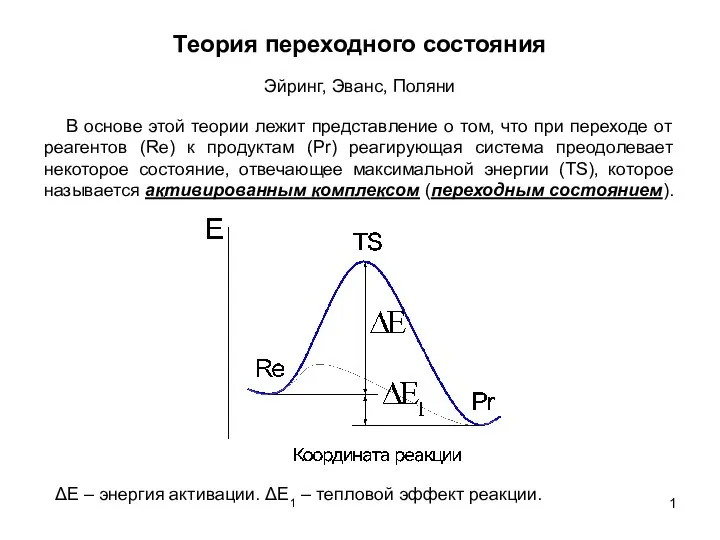 Теория переходного состояния. Эйринг, Эванс, Поляни. (Лекция 5)
Теория переходного состояния. Эйринг, Эванс, Поляни. (Лекция 5) Движение тела по окружности
Движение тела по окружности Презентация по физике "Работа электростатического поля по перемещению заряда" -
Презентация по физике "Работа электростатического поля по перемещению заряда" -  Построение изображений в линзах. Виды линз
Построение изображений в линзах. Виды линз Основы термодинамики
Основы термодинамики Геометрия червячного колеса. Лекция 17
Геометрия червячного колеса. Лекция 17 Презентация на тему Радиоволны
Презентация на тему Радиоволны