Содержание
- 2. 2.1 МЕТОД СИЛ Метод сил – один из общих универсальных методов раскрытия статической неопределимости. Есть ещё
- 3. 2.1 МЕТОД СИЛ Для решения задачи необходимо назначить лишние неизвестные. За лишние можно принять любые неизвестные,
- 4. 2.1 МЕТОД СИЛ Канонические уравнения метода сил, для три раза статически неопределимой системы. Это уравнения совместности
- 5. 2.1 МЕТОД СИЛ - формула для определения δik - Интеграл Мора - формула для определения ∆iF
- 7. Скачать презентацию
Слайд 22.1 МЕТОД СИЛ
Метод сил – один из общих универсальных методов раскрытия статической
2.1 МЕТОД СИЛ
Метод сил – один из общих универсальных методов раскрытия статической

Метод сил позволяет составить уравнения совместности деформаций или уравнения перемещений. Он даёт стандартный подход вне зависимости от вида конструкции.
Неразрезной называют такую балку, которая, не прерываясь, перекрывает несколько пролётов.
Преимущества: больше жёсткость, то есть меньше перемещения и, в большинстве случаев, больше грузоподъёмность.
Недостаток: неразрезная балка – статически неопределимая балка и в ней могут быть монтажные напряжения, связанные с неточной установкой опор. Несмотря на этот недостаток, неразрезные балки широко применяются в конструкциях летательных аппаратов.
Опоры нумеруются 0, 1, 2, 3, 4 (слева направо). На балку действуют активные силы и реакции опор.
У балки три промежуточных опоры и всегда, степень статической неопределимости равна числу промежуточных опор.
Слайд 32.1 МЕТОД СИЛ
Для решения задачи необходимо назначить лишние неизвестные. За лишние можно
2.1 МЕТОД СИЛ
Для решения задачи необходимо назначить лишние неизвестные. За лишние можно

После назначения лишних неизвестных, изображаем основную систему (ОС)
Основной системой (ОС) (б) называют статически определимую и геометрически неизменяемую систему, которая получается из исходной статически неопределимой, после отбрасывания лишних связей и внешних сил. Лишние связи – связи, в которых возникают лишние неизвестные, то есть в нашем случае, лишними связями будут промежуточные опоры. Далее изображаем эквивалентную систему.
Эквивалентная система (ЭС) (в)– это основная система, нагруженная активными силами и лишними неизвестными. Реакцию H0 не показываем, так как из уравнений статики, H0 = 0.
Закономерности деформаций изучаемой системы в том, что в эквивалентной системе, перемещения в направлении "лишних" связей, должны быть равны нулю. Или иначе: Х1, Х2, Х3 должны быть такими, чтобы в сечениях 1, 2, 3 эквивалентной системы прогибы обращались в ноль, то есть
∆1 = 0, ∆2 = 0, ∆3 = 0.
Слайд 42.1 МЕТОД СИЛ
Канонические уравнения метода сил, для три раза статически неопределимой системы.
2.1 МЕТОД СИЛ
Канонические уравнения метода сил, для три раза статически неопределимой системы.

Физический смысл: перемещения в эквивалентной системе, по направлению лишних неизвестных равны нулю.
δik – коэффициенты канонических уравнений – это пе-ремещения в основной системе по направлению i-й лишней связи от единичного силового фактора, соответствующего лишнему неизвестному Xk. При i = k получаем главные коэффициенты или главные податливости основной системы (податливость – перемещение от единичной силы). Если i ≠ k, то это побочные коэффициенты канонических уравнений (побочные податливости). Вспомним о взаимности перемещений (δik = δki). Иначе говоря, матрица коэффициентов канонических уравнений симметрична относительно главной диагонали
Слайд 52.1 МЕТОД СИЛ
- формула для определения δik
- Интеграл Мора
- формула для определения
∆iF
M
2.1 МЕТОД СИЛ
- формула для определения δik
- Интеграл Мора
- формула для определения
∆iF
M

,
.
Для прямолинейных стержней коэффициенты и свободные члены канонических уравнений, можно вычислять способу Верещагина
 Идеальный физический маятник
Идеальный физический маятник Механические колебания. Тест
Механические колебания. Тест Зубчатые передачи
Зубчатые передачи Динамика. Лекция 8
Динамика. Лекция 8 Модели атомов. Атом водорода по теории Бора. Тема 7
Модели атомов. Атом водорода по теории Бора. Тема 7 Статистическая радиотехника. Спектральный метод анализа прохождения стационарного случайного процесса через линейную цепь
Статистическая радиотехника. Спектральный метод анализа прохождения стационарного случайного процесса через линейную цепь Презентация на тему Физика в космосе
Презентация на тему Физика в космосе  Закон Архимеда
Закон Архимеда Механические волны
Механические волны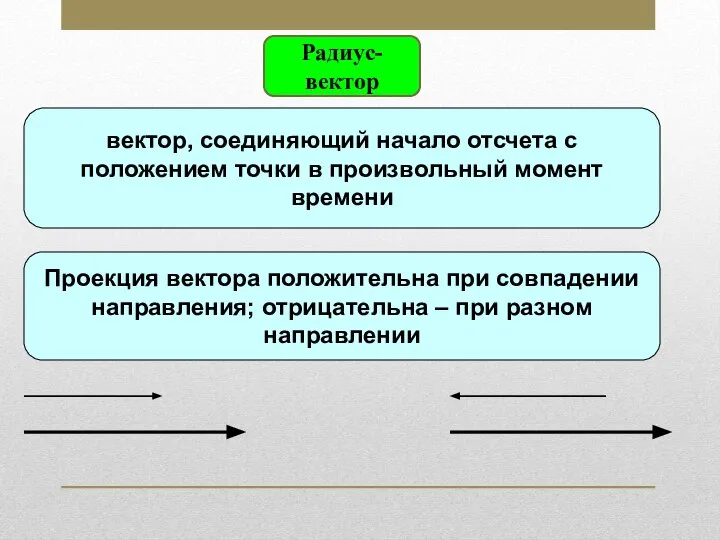 Радиус-вектор. Кинематические характеристики
Радиус-вектор. Кинематические характеристики Уравнения Максвелла
Уравнения Максвелла Молекулярная физика и термодинамика. Тест
Молекулярная физика и термодинамика. Тест Презентация на тему Измерительные приборы
Презентация на тему Измерительные приборы  Презентация на тему Виды сил
Презентация на тему Виды сил  Цепные передачи (ЦП)
Цепные передачи (ЦП) Презентация на тему Инерция (7 класс)
Презентация на тему Инерция (7 класс)  Тепловые явления
Тепловые явления Работа и мощность. Задачи
Работа и мощность. Задачи Управление потоком поверхностных плазмонполяритонов с помощью внешних полей
Управление потоком поверхностных плазмонполяритонов с помощью внешних полей Сущность фотометрических методов
Сущность фотометрических методов Параметры эвольвентного зубчатого зацепления
Параметры эвольвентного зубчатого зацепления О возмущении по крену при совместной работе нескольких ЖРД
О возмущении по крену при совместной работе нескольких ЖРД Тепловые двигатели
Тепловые двигатели Виды сил
Виды сил О создании Комплекса NICA и необходимых расходах до 2022 года
О создании Комплекса NICA и необходимых расходах до 2022 года Сообщающиеся сосуды. Применение сообщающихся сосудов
Сообщающиеся сосуды. Применение сообщающихся сосудов Физика вокруг нас Подготовили: обучающиеся 10 класса
Физика вокруг нас Подготовили: обучающиеся 10 класса Работа силы упругости. Потенциальная энергия упруго деформированного тела
Работа силы упругости. Потенциальная энергия упруго деформированного тела