Содержание
- 2. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. Определим закон движения точки. Н.У.: При
- 3. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. Решение. x 0 t=0 Н.У.: При
- 4. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. Для нахождения высоты подъема точки, найдем
- 5. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. Решение. M Характеристическое уравнение: Н.У.:
- 6. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. Характеристическое уравнение: Н.У.: Уравнения движения точки:
- 7. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. A r M Решение:
- 8. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. Сделаем замену переменных: Характеристическое уравнение:
- 9. МГТУ им. Н.Э. Баумана Динамика точки в инерциальной системе отсчета. Подставляем это решение в уравнение: Н.У.:
- 11. Скачать презентацию








 Регулярные вариации низкочастотных акустических полей
Регулярные вариации низкочастотных акустических полей Электрическая цепь и ее составные
Электрическая цепь и ее составные Колебательный контур
Колебательный контур Квантовая природа света
Квантовая природа света Радиационное излучение
Радиационное излучение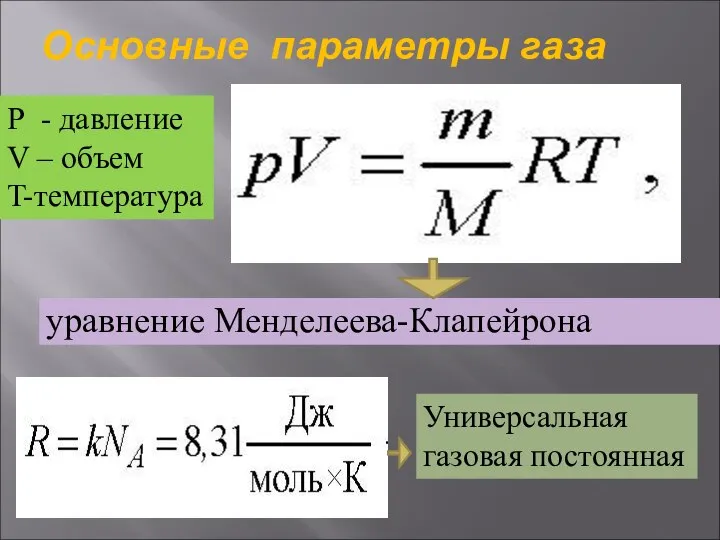 Основные параметры газа
Основные параметры газа Способы соединения частей: шестеренки
Способы соединения частей: шестеренки Явление тяготения. Сила тяжести
Явление тяготения. Сила тяжести Лазеры. Виды лазеров
Лазеры. Виды лазеров Альбом электрических схем для сдачи экзаменов по программе Машинист электропоезда
Альбом электрических схем для сдачи экзаменов по программе Машинист электропоезда Системы высот. Геодезия
Системы высот. Геодезия Классификация тепловых двигателей
Классификация тепловых двигателей Проведение прочностных расчетов машин и механизмов на предприятии
Проведение прочностных расчетов машин и механизмов на предприятии Попов – основатель радиовещания
Попов – основатель радиовещания Обобщающий урок Знатоки физики
Обобщающий урок Знатоки физики Техническое обслуживание смазочной системы МТЗ-80
Техническое обслуживание смазочной системы МТЗ-80 Простые механизмы. КПД
Простые механизмы. КПД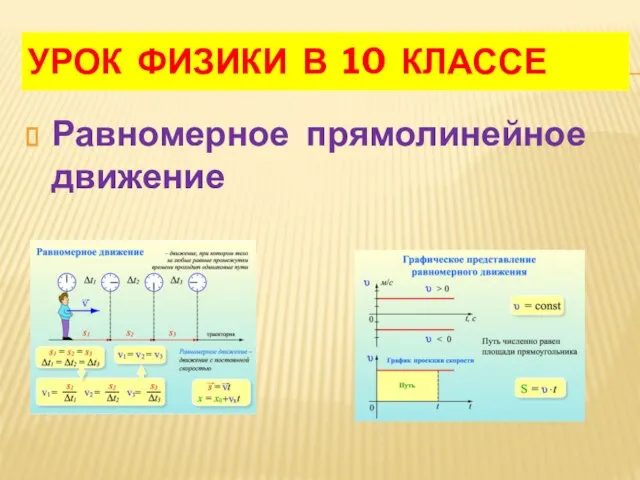 Урок4 РПД
Урок4 РПД Презентация на тему Инерция и инертность
Презентация на тему Инерция и инертность  Наблюдение сплошного и линейчатых спектров. Лабораторная работа
Наблюдение сплошного и линейчатых спектров. Лабораторная работа Полупроводники
Полупроводники OVZ_Zanyatie_3
OVZ_Zanyatie_3 Энергия колебательного движения
Энергия колебательного движения Современные требования к проектной документации по размещению передающих радиотехнических объектов
Современные требования к проектной документации по размещению передающих радиотехнических объектов Презентация на тему Колебательный контур. Электромагнитные колебания
Презентация на тему Колебательный контур. Электромагнитные колебания  Презентация на тему Теплопередача и ее виды
Презентация на тему Теплопередача и ее виды  Основное уравнение динамики вращательного движения твердого тела. (Лекция 7)
Основное уравнение динамики вращательного движения твердого тела. (Лекция 7) Физика плазмы
Физика плазмы