Содержание
- 2. Составим отношение и перейдем к пределу, устремив ε к 0, полученный предел назовем производной ϕ по
- 3. Если мы определим вектор, составляющие которого по основным ортам есть , то его составляющая по любому
- 4. Из других обозначений градиента ϕ укажем, как наиболее употребляемое, ∇ϕ, где знак ∇ читается «набла». При
- 5. Проведем через точку М поверхность уровня функции ϕ и докажем, что вектор градиента ϕ направлен по
- 6. Если бы луч Ms' не пересекал сферу, то, продолжив его в другую сторону, мы нашли бы
- 7. Разберем несколько примеров вычисления градиента. Самым важным случаем является тот, когда ϕ зависит только от расстояния
- 9. Скачать презентацию
Слайд 2 Составим отношение и перейдем к пределу, устремив ε к 0, полученный
Составим отношение и перейдем к пределу, устремив ε к 0, полученный

предел назовем производной ϕ по направлению s в точке М и обозначим через
и так как
Знание производной для любого направления s позволяет вычислить во
всех точках, соседних с точкой М, значение функции ϕ с точностью до членов второго порядка малости.
то получается соотношение:
Для вычисления введем систему координат х, у, z и заметим, что
функция ϕ (х, у, z) будет сложной функцией от s через посредство х, у, z. По правилу дифференцирования сложных функций мы получим
(9.5)
(9.6)
(9.8)
(9.9)
Слайд 3 Если мы определим вектор, составляющие которого по основным ортам есть
,
Если мы определим вектор, составляющие которого по основным ортам есть
,

Назовем этот вектор градиентом ϕ в точке М и обозначим символом grad ϕ. Его составляющие
Таким образом
вспомним правило преобразования составляющих вектора а
Этот вектор не зависит от выбора системы координат х, у, z, так как его составляющие по любому направлению были определены непосредственно.
Величина grad ϕ равна
Производная по любому направлению s равна проекции grad ϕ на это направление, следовательно
(9.10)
(9.11)
(9.12)
(9.13)
Слайд 4 Из других обозначений градиента ϕ укажем, как наиболее употребляемое, ∇ϕ, где
Из других обозначений градиента ϕ укажем, как наиболее употребляемое, ∇ϕ, где

который, будучи применен к скаляру ϕ, дает grad ϕ. Этот оператор, можно рассматривать также как символический вектор. Его называют иногда оператором Гамильтона.
Из этой формулы видно, что ∇ является дифференциальным оператором.
Из этой формулы видно, что достигает наибольшего значения для направления s, совпадающего как раз с направлением grad ϕ, причем это наибольшее значение равно величине grad ϕ. Поэтому можно дать другое определение градиента:
Градиентом ϕ называется вектор, имеющий направление быстрейшего увеличения ϕ и по величине равный производной по этому направлению.
(9.14)
(9.15)
(9.16)
Слайд 5 Проведем через точку М поверхность уровня функции ϕ и докажем, что
Проведем через точку М поверхность уровня функции ϕ и докажем, что

СВОЙСТВА ВЕКТОРА grad ϕ
Так как на поверхности уровня ϕ = const, то производная по всякому направлению s, лежащему в касательной плоскости к поверхности уровня в точке М, равна нулю, следовательно, для всякого такого направления по (9.14)
что может быть только, если grad ϕ перпендикулярен к поверхности уровня в точке М.
Проведем через точку М (рис. 10.1) поверхность уровня ϕ = const, к этой поверхности уровня восставим в точке М нормаль MN и отложим по этой нормали вектор
.
grad ϕ направлен в ту сторону нормали, куда ϕ возрастает.
Связь между градиентом функции ϕ и производной от ϕ по различным направлениям имеет очень простое геометрическое истолкование.
(10.1)
Слайд 6 Если бы луч Ms' не пересекал сферу, то, продолжив его в
Если бы луч Ms' не пересекал сферу, то, продолжив его в

Из формулы
Если единичный вектор нормали к поверхности уровня обозначить через n, а
производную от функции ϕ по направлению этой нормали через , то, очевидно, будет
Построим далее на MN, как на диаметре, сферу и рассмотрим какой-нибудь луч Ms, проходящий через точку М и имеющий направление s. Пусть этот луч пересечет сферу в точке K.
Так как угол при K в Δ MNK есть прямой (по известному свойству окружности), то МK является проекцией MN на направление Ms; но проекция grad ϕ на какое-либо направление есть производная ϕ по этому направлению, следовательно, мы получаем, что
вытекает, если через d r = s ds обозначить бесконечно малый вектор, идущий из точки М в направлении s, следующее соотношение:
(10.2)
(10.3)
Слайд 7 Разберем несколько примеров вычисления градиента.
Самым важным случаем является тот, когда
Разберем несколько примеров вычисления градиента. Самым важным случаем является тот, когда

а направлен grad ϕ в ту сторону, куда ϕ возрастает, т. е. при положительном
ϕ' (r) ортом grad ϕ служит , а при отрицательном ϕ' (r) ортом grad ϕ является -
Пусть . Поверхностями уровня служат концентрические сферы с центром в начале координат. Нормаль к поверхности уровня совпадает с радиусом-вектором, поэтому по величине grad ϕ равен
Если мы найдем такой вектор а, что для произвольного dr будет
то можем утверждать, что а = grad ϕ, ибо d ϕ = dr∙a = dr∙ grad ϕ приводит к соотношению dr∙ (a − grad ϕ) = 0; откуда видно, что а − grad ϕ перпендикулярно к любому направлению, что может быть только, если а = grad ϕ.
(10.4)
Таким образом, всегда будет
(10.5)
Докажем основные в теории градиента формулы
(10.3*)
 prezentaciya_chto_izuchaet_fizika
prezentaciya_chto_izuchaet_fizika Комплексная механизация лесовосстановительных работ в Огудневском участковом лесничестве
Комплексная механизация лесовосстановительных работ в Огудневском участковом лесничестве Динамика вращения. Закон динамики вращения
Динамика вращения. Закон динамики вращения Физика в жизни
Физика в жизни Радиоактивные превращения, ядерные реакции, энергия связи. Решение задач
Радиоактивные превращения, ядерные реакции, энергия связи. Решение задач Полупроводниковые приборы
Полупроводниковые приборы Физическая кинетика явления переноса (лекция № 15)
Физическая кинетика явления переноса (лекция № 15) Компенсация реактивной мощности
Компенсация реактивной мощности Тепловая генерация энергии на основе холодного ядерного синтеза
Тепловая генерация энергии на основе холодного ядерного синтеза Электромагнитные колебания. Превращение энергии в колебательном контуре
Электромагнитные колебания. Превращение энергии в колебательном контуре Получение электричества с помощью волос
Получение электричества с помощью волос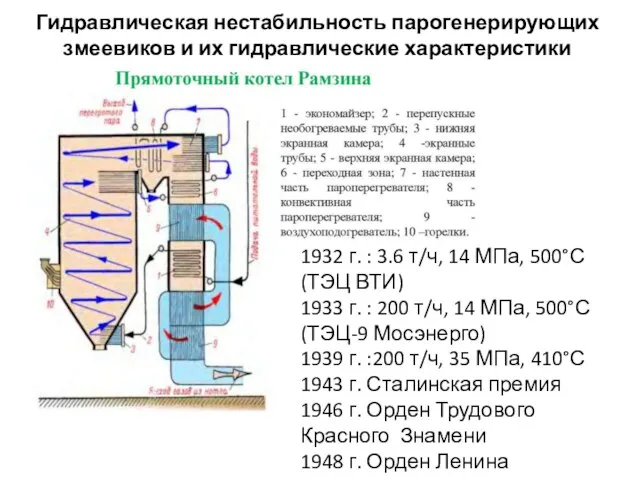 Гидравлическая нестабильность парогенерирующих змеевиков и их гидравлические характеристики
Гидравлическая нестабильность парогенерирующих змеевиков и их гидравлические характеристики Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю
Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю Применение переменного тока. (Лекция 9)
Применение переменного тока. (Лекция 9) Температура. Виды термометров
Температура. Виды термометров Prezentatsia_5
Prezentatsia_5 Поляризация света. Голография. Лекция 16-17
Поляризация света. Голография. Лекция 16-17 Презентация на тему Электромагнитные волны
Презентация на тему Электромагнитные волны  Обратимые и необратимые термодинамические процессы. (Лекция 8)
Обратимые и необратимые термодинамические процессы. (Лекция 8) Первый в мире паровой поезд когда и кем был изобретен
Первый в мире паровой поезд когда и кем был изобретен Расчет деревянных балок
Расчет деревянных балок Презентация на тему Затухающие колебания
Презентация на тему Затухающие колебания  Как сберечь тепло в доме
Как сберечь тепло в доме Периодическое движение
Периодическое движение Строительство и эксплуатация зданий и сооружений. Связи и их реакции
Строительство и эксплуатация зданий и сооружений. Связи и их реакции Связи и реакции связей
Связи и реакции связей Квантовая теория. Свойства операторов и принцип неопределенности Гейзенберга
Квантовая теория. Свойства операторов и принцип неопределенности Гейзенберга Устройство ведущего моста трактора ДТ-75
Устройство ведущего моста трактора ДТ-75