Волновая оптика

Временная – согласованность волн в данной области пространства в разные моменты времени, ограничивается степенью монохроматичности света.
Пространственная – согласованность волн в разных областях в один и тот же момент времени, ограничивается дли-ной пространственной когерентности.
типы когерентности :
‘

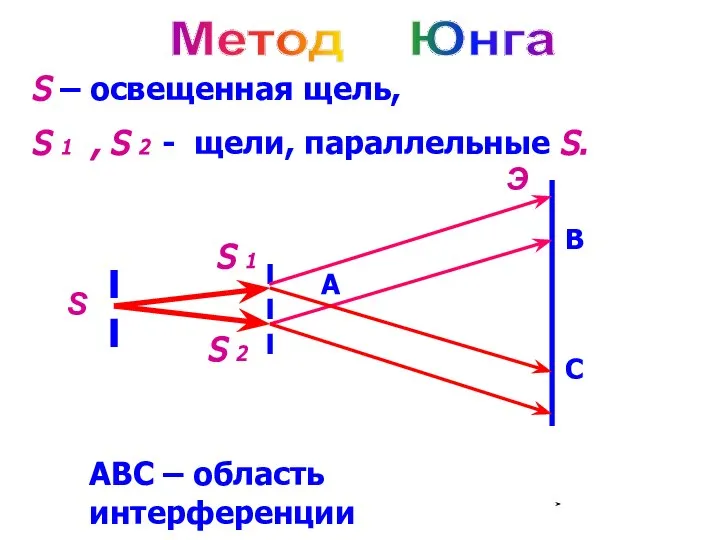
S
Э
Метод Юнга
S – освещенная щель,
S 1 , S 2 - щели, параллельные S.
S 1
S 2
А
В
С
АВС – область интерференции

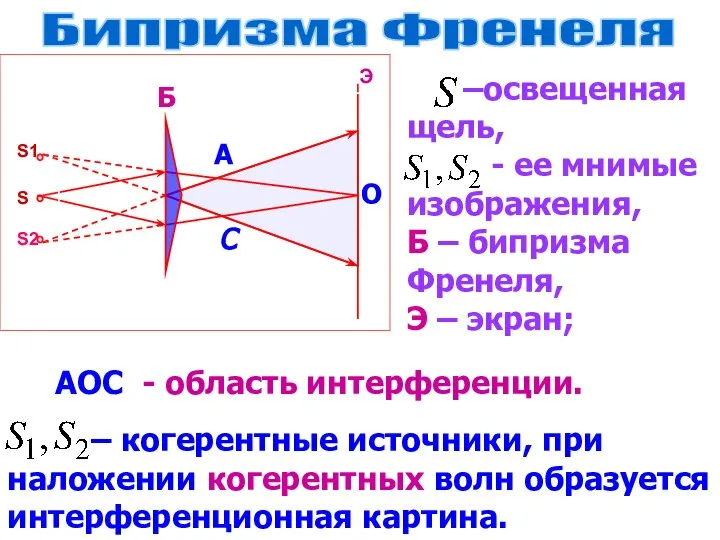
Бипризма Френеля
–освещенная щель,
- ее мнимые изображения,
Б – бипризма Френеля,
Э – экран;
Б
– когерентные источники, при наложении когерентных волн образуется интерференционная картина.
АОС - область интерференции.
А
О
С

Геометрическая разность хода
оптическая разность хода
Условие max:
Условие min:
- целое число.

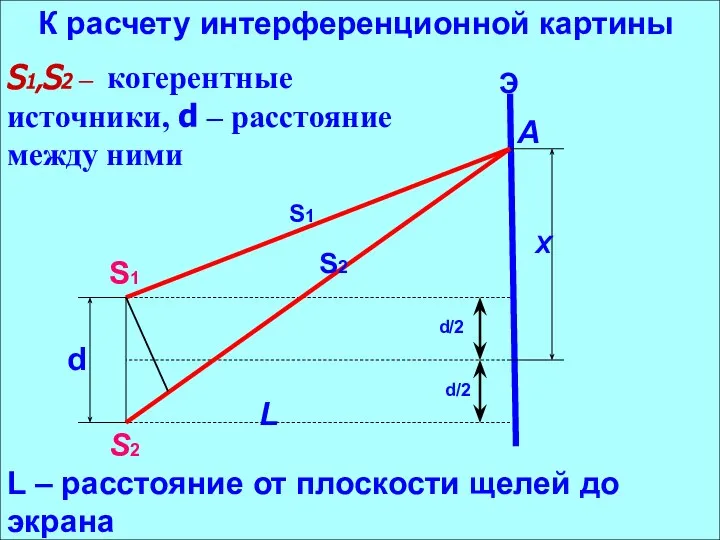
S1,S2 – когерентные источники, d – расстояние между ними
К расчету интерференционной картины
L – расстояние от плоскости щелей до экрана

Х –координата max или min на экране,
– расстояние от источников до А.
-

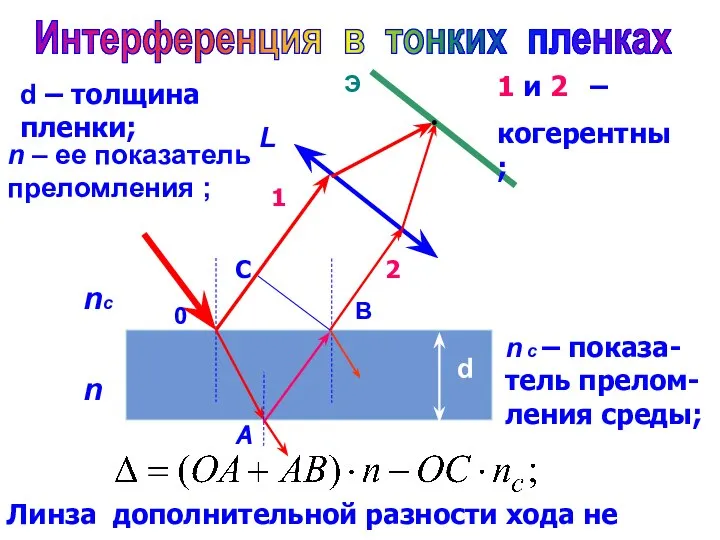
n
nс
0
B
d
L
Э
А
С
1
2
1 и 2 –
когерентны;
Линза дополнительной разности хода не вносит.
n c – показа-тель прелом-ления среды;
n – ее показатель преломления ;
d – толщина пленки;
Интерференция в тонких пленках

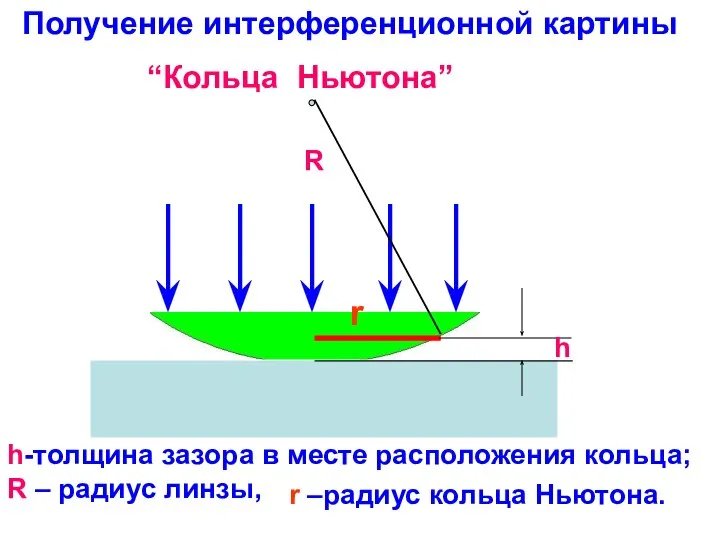
r
R
h
Получение интерференционной картины
“Кольца Ньютона”
R – радиус линзы,
r –радиус кольца Ньютона.
h-толщина зазора в месте расположения кольца;

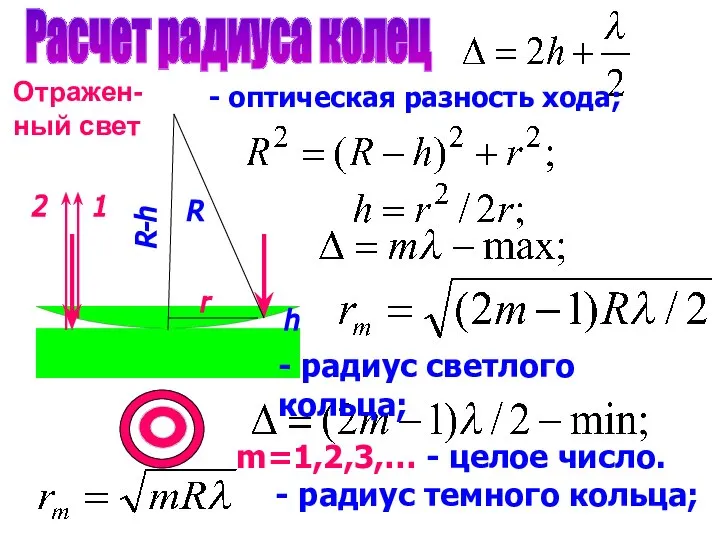
Расчет радиуса колец
R
r
h
R-h
1
2
- оптическая разность хода;
- радиус светлого кольца;
- радиус темного кольца;
m=1,2,3,… - целое число.
Отражен-ный свет

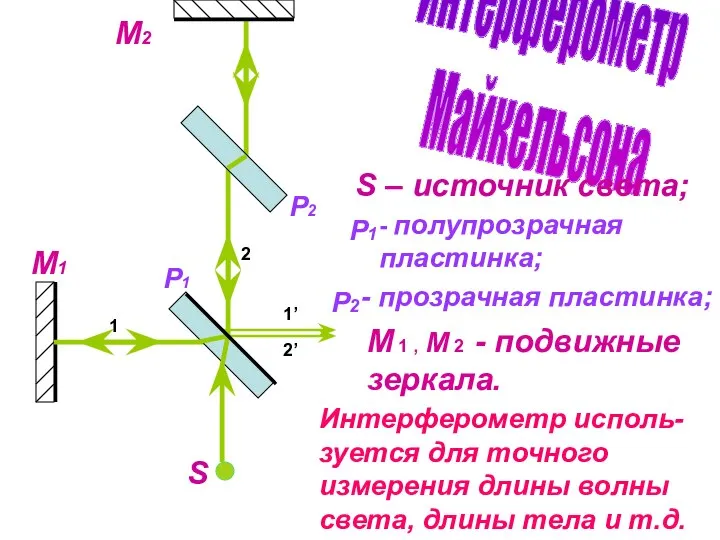
P2
P1
1
2
1’
2’
Интерферометр
Майкельсона
S
S – источник света;
P2
P1
- полупрозрачная пластинка;
М 1 , М 2 - подвижные зеркала.
М1
М2
- прозрачная пластинка;
Интерферометр исполь-зуется для точного измерения длины волны света, длины тела и т.д.

Дифракция Френеля:
фронт волны – сферический или плоский; на экране, находящемся на конечном расстоянии от пре-пятствия, «дифракционное изображение» препятствия.

Дифракция Фраунгофера:
фронт волны - плоский;
на экране, находящемся в
фокальной плоскости линзы, “ дифракционное изображе-ние” удаленного источника света.

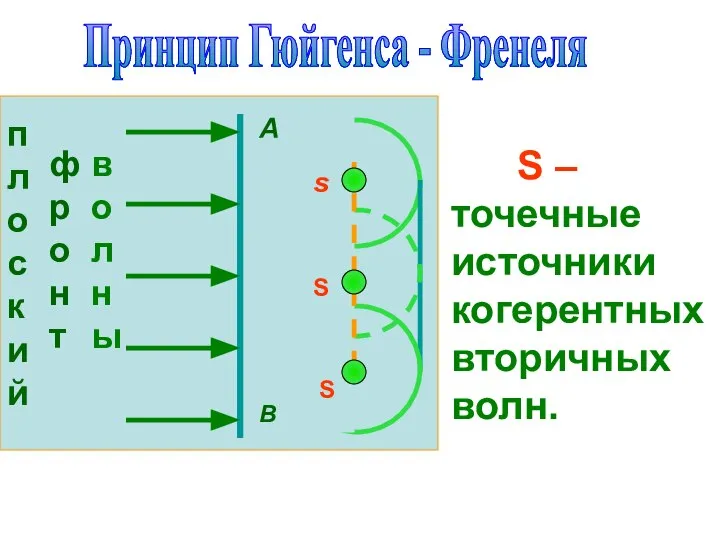
Принцип Гюйгенса - Френеля
А
В
s
S
S
S – точечные источники когерентных вторичных волн.
плоский
фронт
волны

Каждая точка среды, до которой
дошел волновой фронт, стано-вится точечным источником вторичных волн. Принцип Гюйгенса - Френеля
Для электромагнитных волн
наличие среды необязательно.

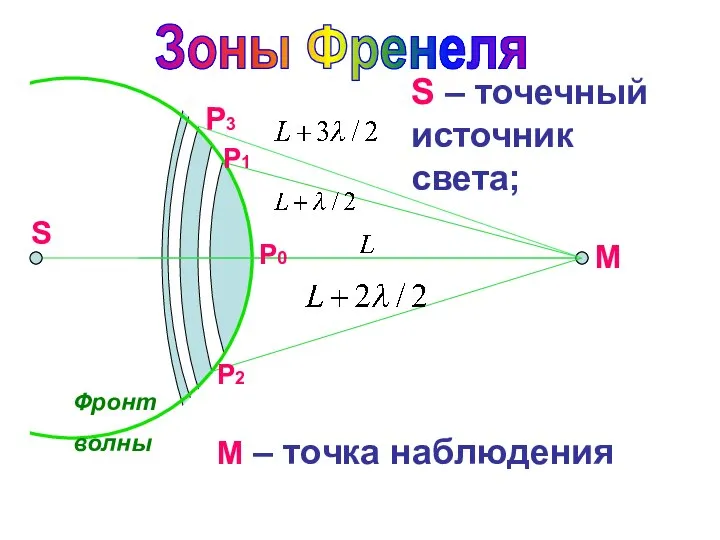
S
Фронт
волны
Р0
Р1
Р2
Р3
Зоны Френеля
М
S – точечный источник света;
М – точка наблюдения

Это участки волновой поверх-
ности, на которые она мыслен-
но разбивается. Площади зон
примерно одинаковы. Колеба-
ния, возбуждаемые в точке М
соседними зонами, противо-
положны по фазе (разность
хода от симметричных точек
равна половине длины волны).

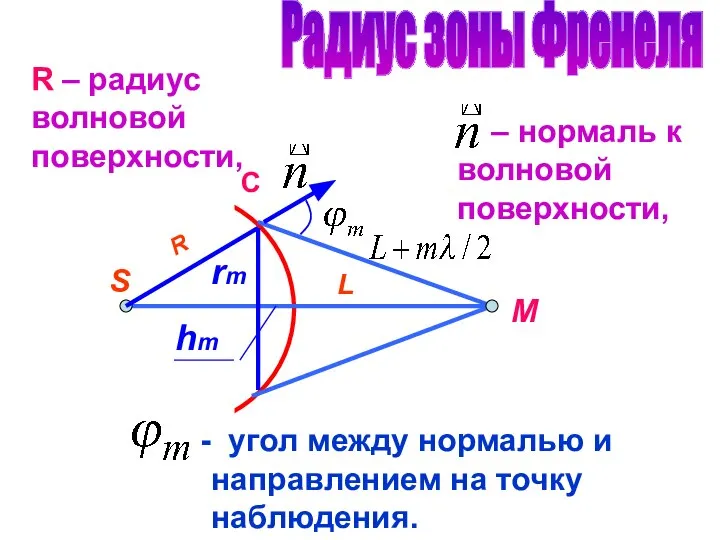
S
R
L
M
Радиус зоны Френеля
rm
hm
R – радиус волновой поверхности,
– нормаль к волновой поверхности,
С
угол между нормалью и направлением на точку наблюдения.

- радиус m-ой зоны.
- высота шарового
сегмента,
При

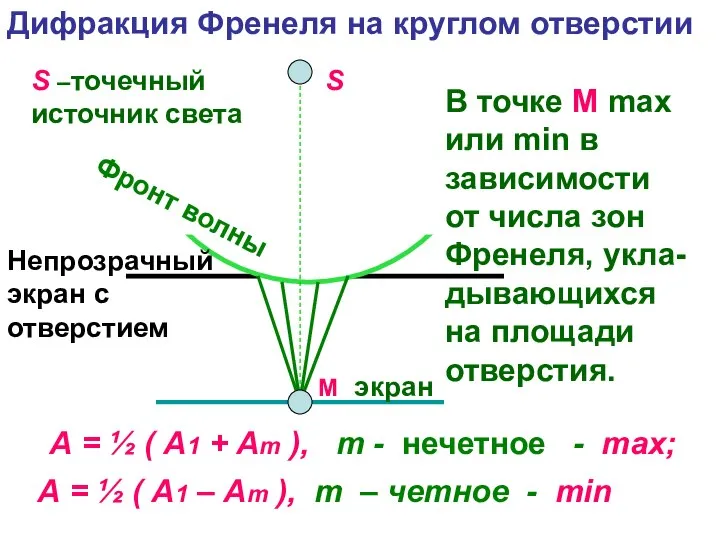
S
М экран
Непрозрачный экран с отверстием
S –точечный источник света
Фронт волны
А = ½ ( А1 + Аm ), m - нечетное - max;
А = ½ ( А1 – Аm ), m – четное - min
В точке М mах или min в зависимости от числа зон Френеля, укла-дывающихся на площади отверстия.
Дифракция Френеля на круглом отверстии

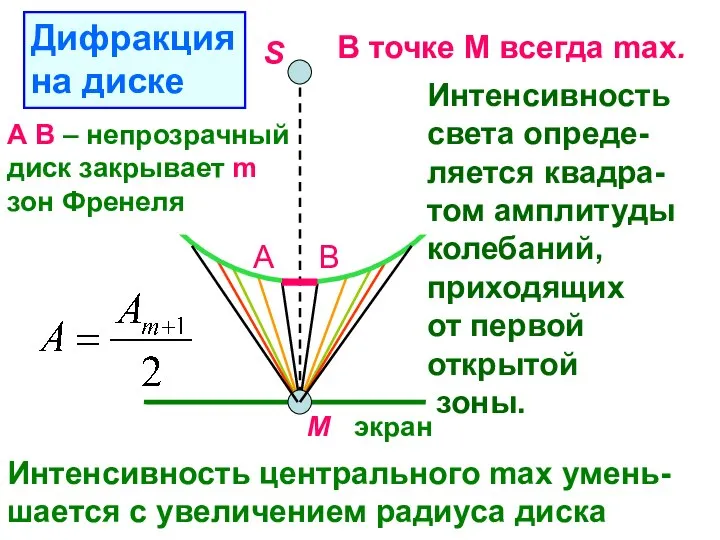
S
М экран
А
В
А В – непрозрачный диск закрывает m зон Френеля
В точке М всегда max.
Интенсивность света опреде-ляется квадра-том амплитуды колебаний, приходящих
от первой открытой
зоны.
Интенсивность центрального max умень-шается с увеличением радиуса диска
Дифракция
на диске

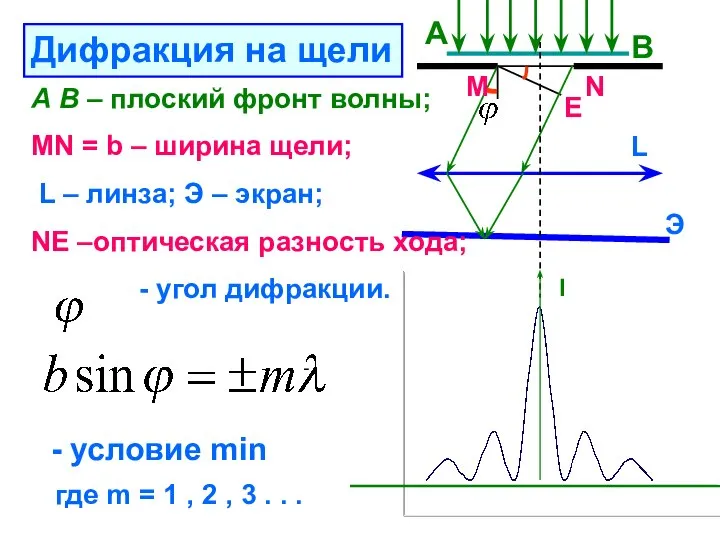
L
А
В
А В – плоский фронт волны;
MN = b – ширина щели;
L – линза; Э – экран;
NE –оптическая разность хода;
- угол дифракции.
I
-
- условие min
где m = 1 , 2 , 3 . . .
Дифракция на щели

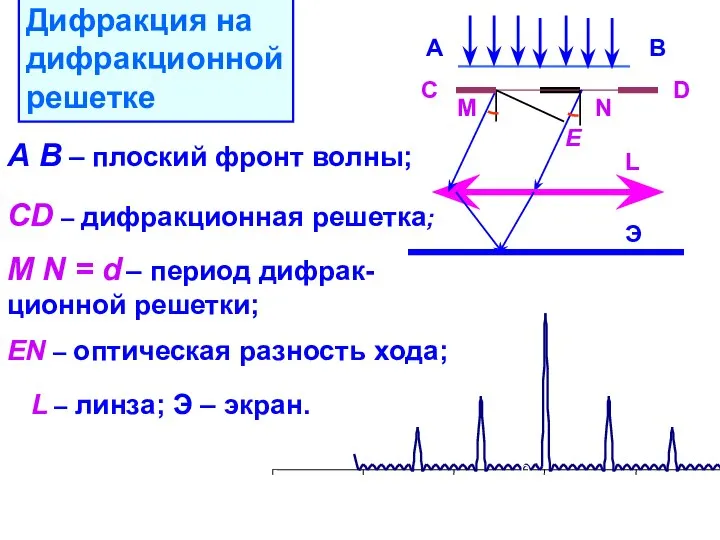
Э
С
D
E
M
N
А
В
L
А В – плоский фронт волны;
CD – дифракционная решетка;
M N = d – период дифрак-ционной решетки;
EN – оптическая разность хода;
L – линза; Э – экран.
Дифракция на
дифракционной
решетке

m = 0 , 1 , 2 , 3 . . .
m = 1, 2 , 3 . . .
Условие главных максимумов:
Условие главных минимумов:

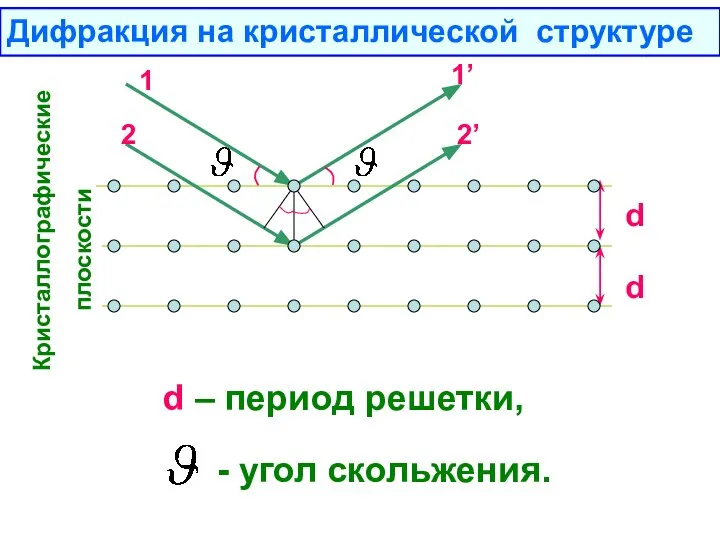
d
d
1
2
2’
1’
Кристаллографические
плоскости
- угол скольжения.
d – период решетки,
Дифракция на кристаллической структуре