Lektsia_8_Kolebania_ZS

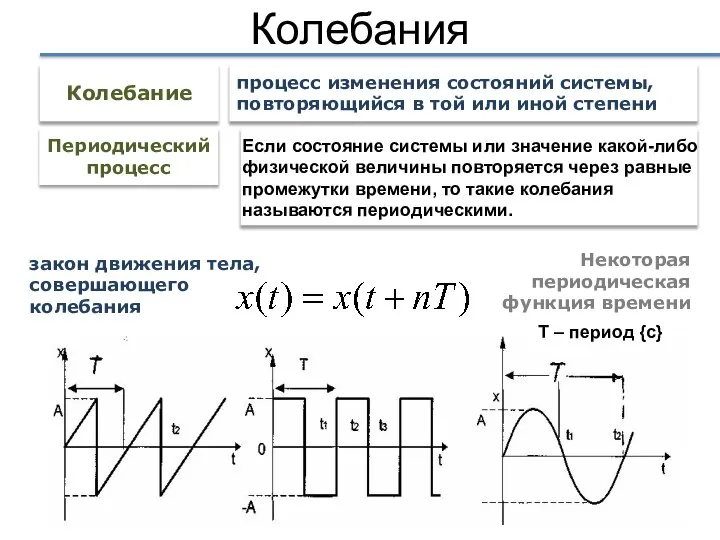
Колебания − это физические процессы, характеризующиеся той или иной степенью повторяемости во времени.

Колебания
закон движения тела,
совершающего колебания
Некоторая
периодическая
функция времени
Периодический
процесс
Колебание
процесс изменения состояний системы,
повторяющийся в той или иной степени
Если состояние системы или значение какой-либо физической величины повторяется через равные промежутки времени, то такие колебания называются периодическими.
T – период {с}

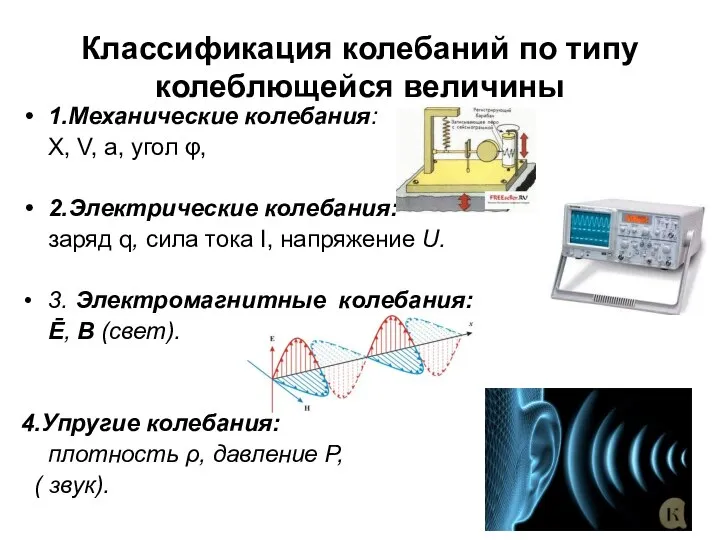
Классификация колебаний по типу колеблющейся величины
1.Механические колебания:
X, V, a, угол φ,
2.Электрические колебания:
заряд q, сила тока I, напряжение U.
3. Электромагнитные колебания:
Ē, В (свет).
4.Упругие колебания:
плотность ρ, давление Р,
( звук).

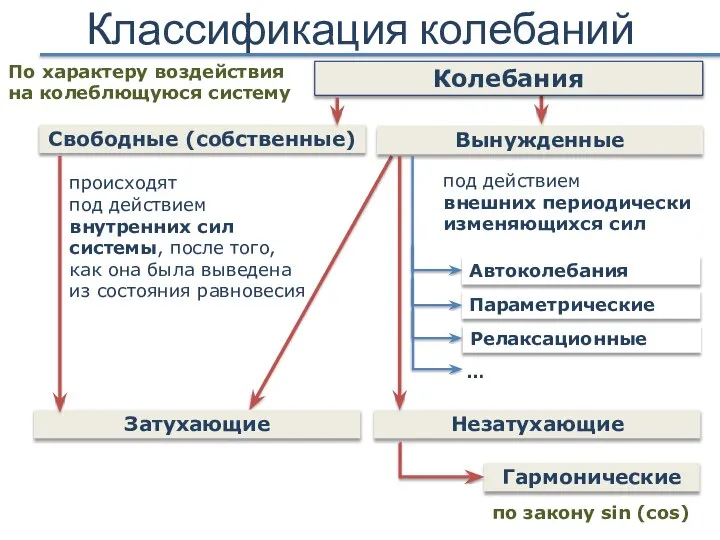
Классификация колебаний
Автоколебания
Свободные (собственные)
Вынужденные
Затухающие
Гармонические
происходят
под действием
внутренних сил системы, после того,
как она была выведена
из состояния равновесия
по закону sin (cos)
Незатухающие
под действием
внешних периодически изменяющихся сил
Параметрические
…
Релаксационные
Колебания
По характеру воздействия на колеблющуюся систему

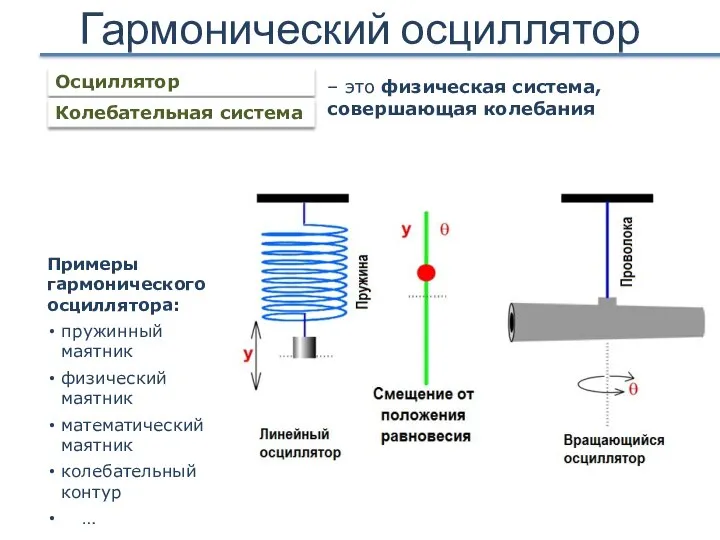
Гармонический осциллятор
Осциллятор
Примеры гармонического осциллятора:
пружинный маятник
физический маятник
математический маятник
колебательный контур
…
Колебательная система
– это физическая система, совершающая колебания

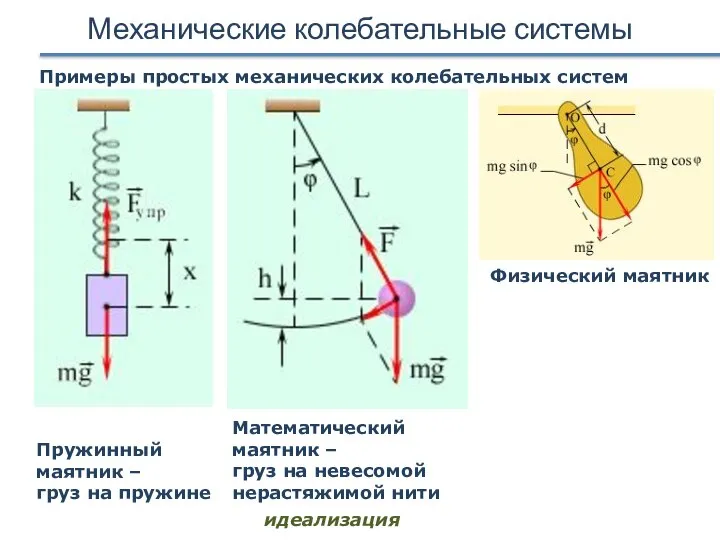
Механические колебательные системы
Примеры простых механических колебательных систем
Пружинный
маятник –
груз на пружине
Математический маятник –
груз на невесомой нерастяжимой нити
Физический маятник
идеализация

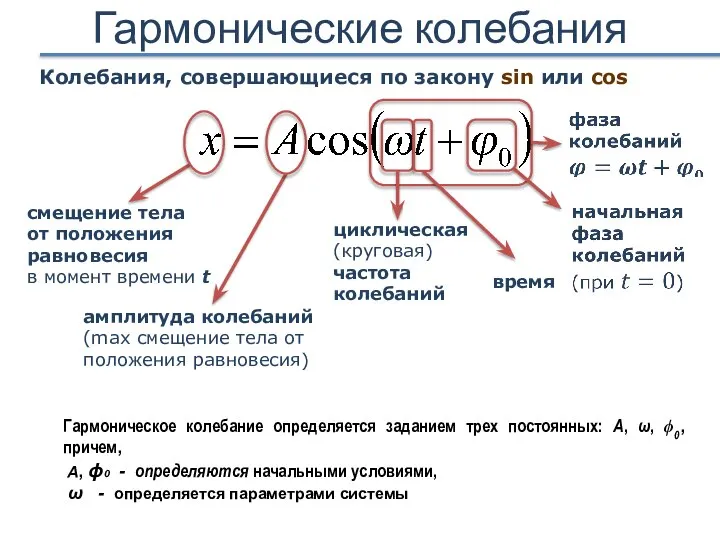
Гармонические колебания
Колебания, совершающиеся по закону sin или cos
смещение тела
от положения равновесия в момент времени t
амплитуда колебаний (max смещение тела от положения равновесия)
циклическая (круговая) частота колебаний
время
Гармоническое колебание определяется заданием трех постоянных: А, ω, ϕ0, причем,
А, ϕ0 - определяются начальными условиями,
ω - определяется параметрами системы

Характеристики колебательного движения
смещение тела от положения равновесия
Амплитуда колебаний
циклическая (круговая) частота колебаний
время колебаний
фаза колебаний
начальная фаза колебаний
(при t=0)
Период колебаний
время, в течение которого
происходит одно полное колебание
максимальное смещение тела
от положения равновесия
Частота колебаний
количество колебаний
в единицу времени
[Т]=с
фаза колебания получает приращение 2π
[ν]=с-1=Гц
,
,

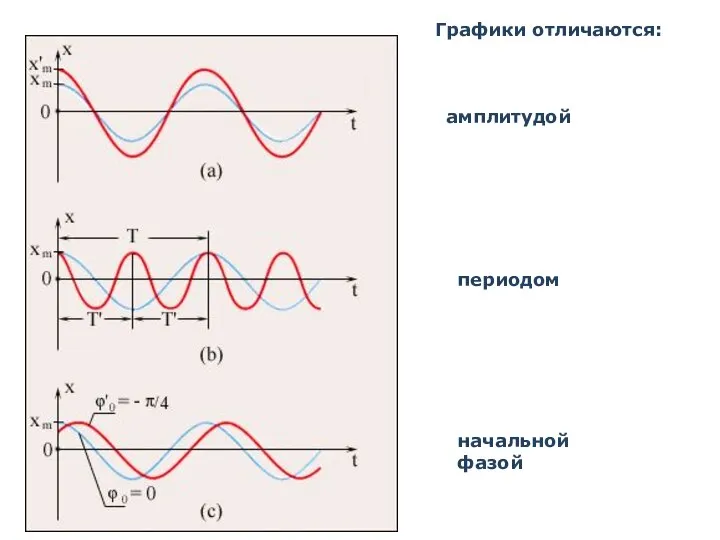
Графики отличаются:
амплитудой
периодом
начальной фазой

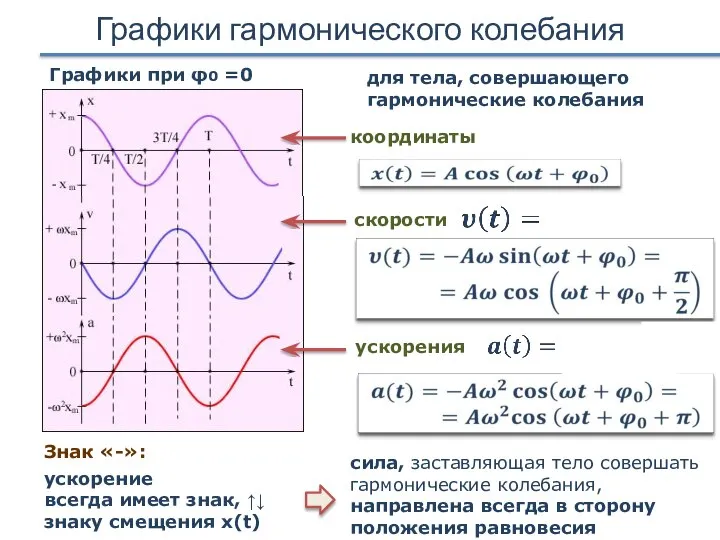
Графики гармонического колебания
Графики при φ0 =0
ускорения
координаты
скорости
для тела, совершающего гармонические колебания
Знак «-»:
сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия
ускорение
всегда имеет знак, ↑↓ знаку смещения x(t)

Квазиупругие силы
Чтобы система совершала гармонические колебания необходимо и достаточно, чтобы единственная сила, действующая в ней была КВАЗИУПРУГАЯ, т.е. сила
Таким свойством обладает упругая сила
в пределах применимости закона Гука
Силы любой другой физической природы, удовлетворяющие этому условию называют квазиупругими
Теорема:
стремящаяся возвратить тело в положение равновесия
пропорциональная смещению тела
из положения равновесия колебаний
направленная в сторону, ↑↓ смещению
с другой стороны, по II з-ну Ньютона

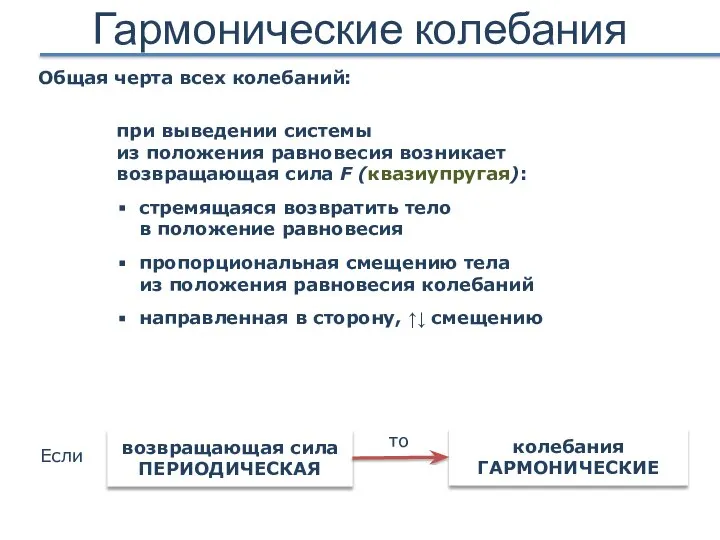
Гармонические колебания
Общая черта всех колебаний:
при выведении системы
из положения равновесия возникает возвращающая сила F (квазиупругая):
стремящаяся возвратить тело
в положение равновесия
пропорциональная смещению тела
из положения равновесия колебаний
направленная в сторону, ↑↓ смещению
Если
колебания ГАРМОНИЧЕСКИЕ
возвращающая сила ПЕРИОДИЧЕСКАЯ
то

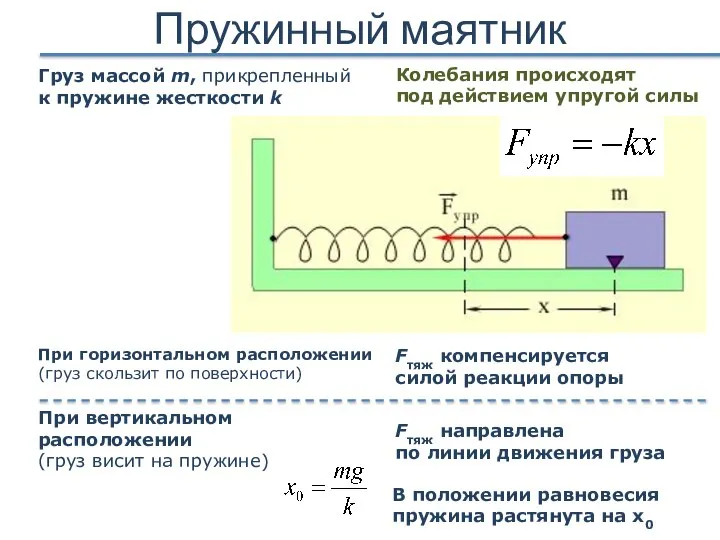
Пружинный маятник
Груз массой m, прикрепленный
к пружине жесткости k
При горизонтальном расположении
(груз скользит по поверхности)
При вертикальном расположении
(груз висит на пружине)
Под действием какой силы происходят колебания?
Колебания происходят
под действием упругой силы
Fтяж компенсируется
силой реакции опоры
Fтяж направлена
по линии движения груза
В положении равновесия
пружина растянута на х0

Пружинный маятник
Период гармонических колебаний груза на пружине
Круговая частота колебаний ω0
Потенциальная энергия
II з-н Ньютона
Дифференциальное уравнение:
где
Решение диф.уравн.
Закон Гука

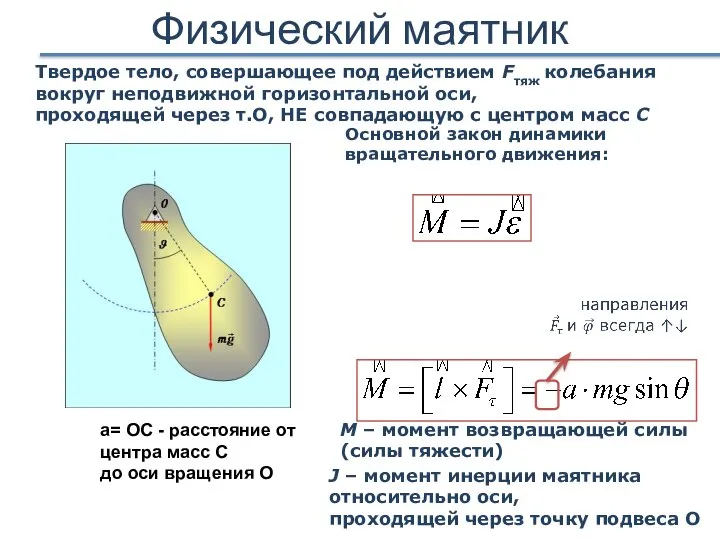
Физический маятник
Твердое тело, совершающее под действием Fтяж колебания вокруг неподвижной горизонтальной оси, проходящей через т.О, НЕ совпадающую с центром масс C
Основной закон динамики
вращательного движения:
М – момент возвращающей силы (силы тяжести)
J – момент инерции маятника относительно оси,
проходящей через точку подвеса О
a= ОС - расстояние от
центра масс С
до оси вращения О

Физический маятник
для малых углов
Период колебаний
Круговая частота
приведенная длина физического маятника
Дифференциальное уравнение колебаний
длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника
,

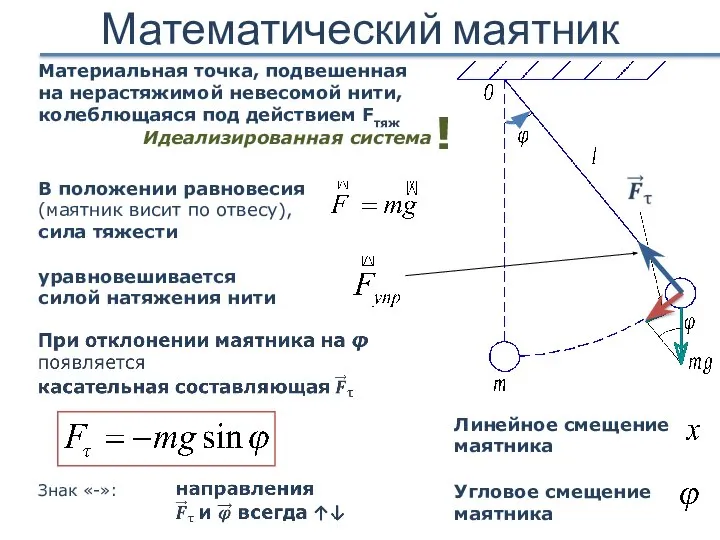
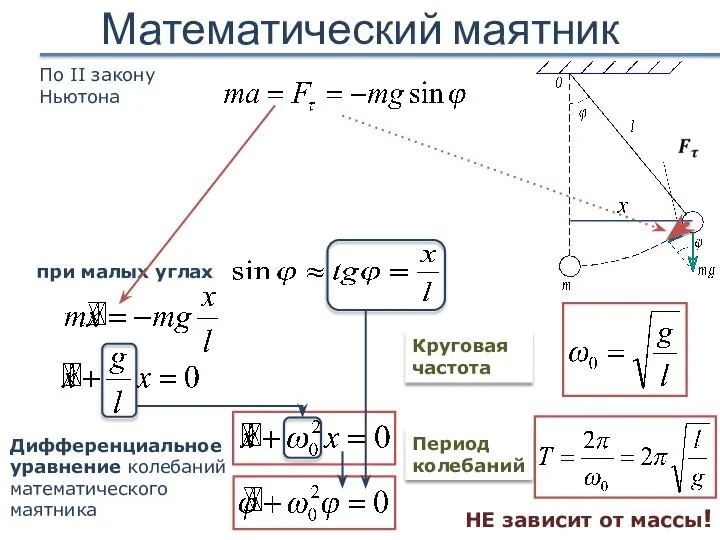
Математический маятник
Материальная точка, подвешенная
на нерастяжимой невесомой нити, колеблющаяся под действием Fтяж
Идеализированная система
!
В положении равновесия
(маятник висит по отвесу), сила тяжести
уравновешивается силой натяжения нити
Угловое смещение маятника
Линейное смещение маятника
Знак «-»:

Математический маятник
По II закону Ньютона
при малых углах
Дифференциальное уравнение колебаний математического маятника
Круговая частота
Период колебаний
НЕ зависит от массы!

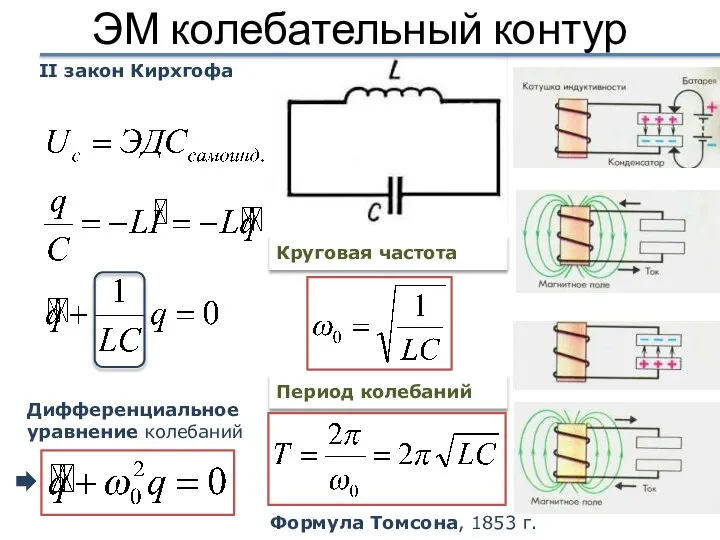
ЭМ колебательный контур
II закон Кирхгофа
Дифференциальное уравнение колебаний
Период колебаний
Круговая частота
Формула Томсона, 1853 г.

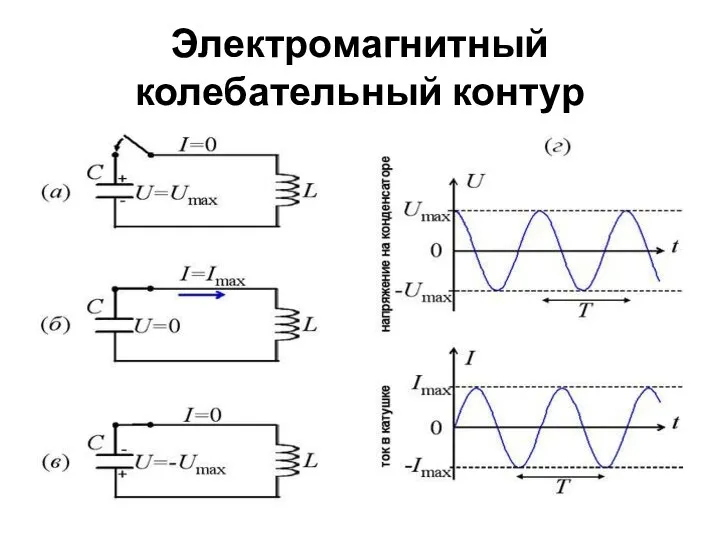
Электромагнитный колебательный контур

ЗСЭ: ЭМ колебания
Колебания заряда
Колебания тока
Колебания напряжения

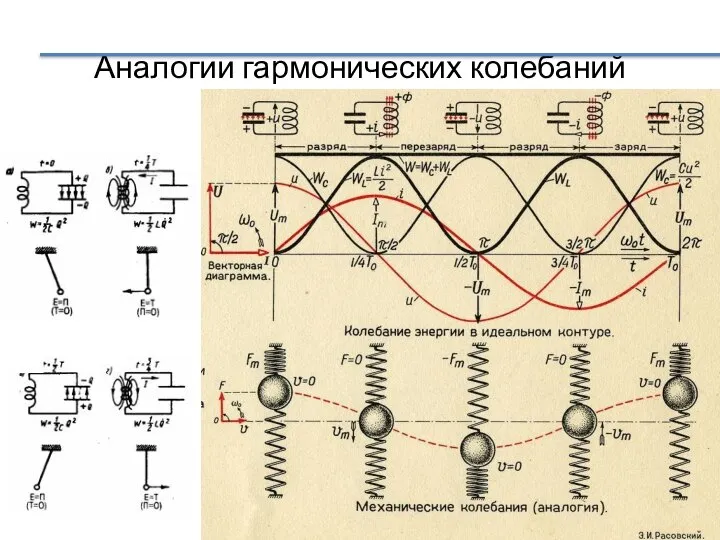
Аналогии гармонических колебаний

Аналогия между механическими и электрическими колебаниями
Механические
колебания
1. x, φ –смещение
2. V -линейная скорость
3. m –масса
4. k –коэффициент жесткости
Электрические
колебания
1. q, U-заряд, напряжение
2. I –сила тока
3. L –индуктивность
4. 1/С.

Гармонический осциллятор
Итак, дифференциальное уравнение гармонического осциллятора:
Решение
этого уравнения:
Уравнение гармонических колебаний
Другие виды записи

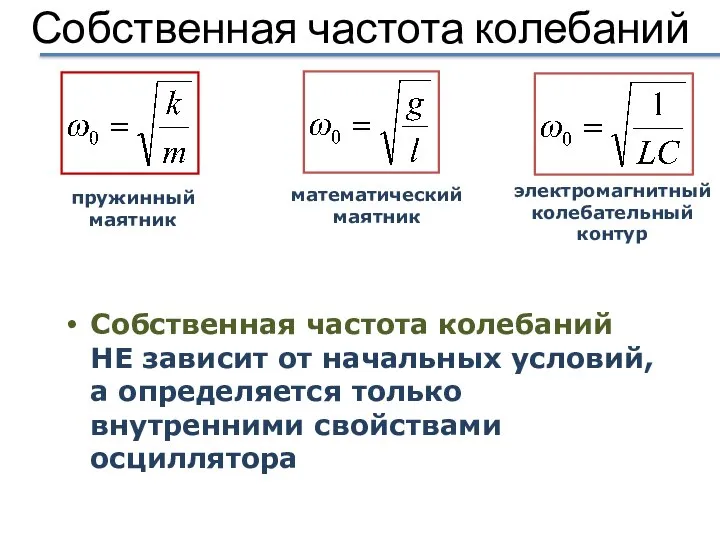
Собственная частота колебаний
От каких параметров зависит собственная частота колебаний?
пружинный маятник
математический маятник
электромагнитный колебательный контур
Собственная частота колебаний
НЕ зависит от начальных условий,
а определяется только
внутренними свойствами осциллятора

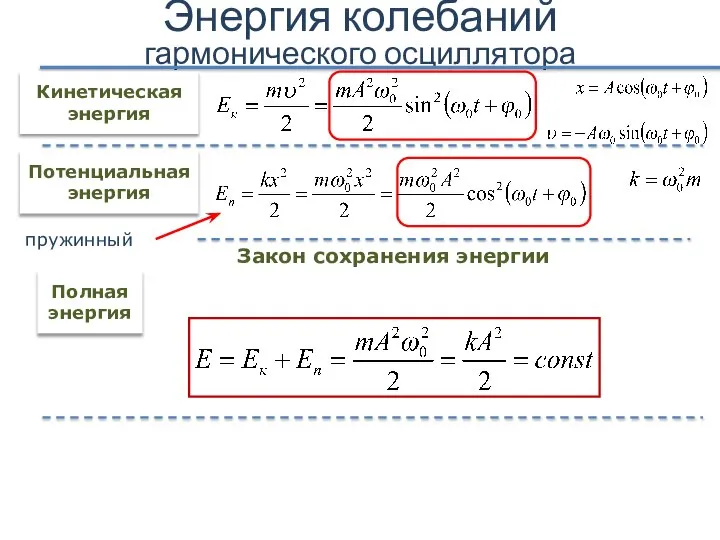
Энергия колебаний
гармонического осциллятора
Кинетическая энергия
Потенциальная энергия
Полная энергия
Закон сохранения энергии
пружинный

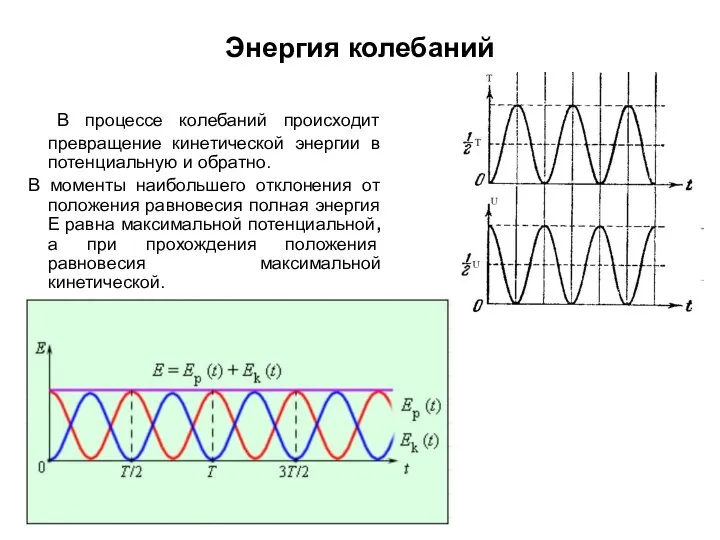
Энергия колебаний
В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно. В моменты наибольшего отклонения от положения равновесия полная энергия Е равна максимальной потенциальной, а при прохождения положения равновесия максимальной кинетической.

Сложение
колебаний

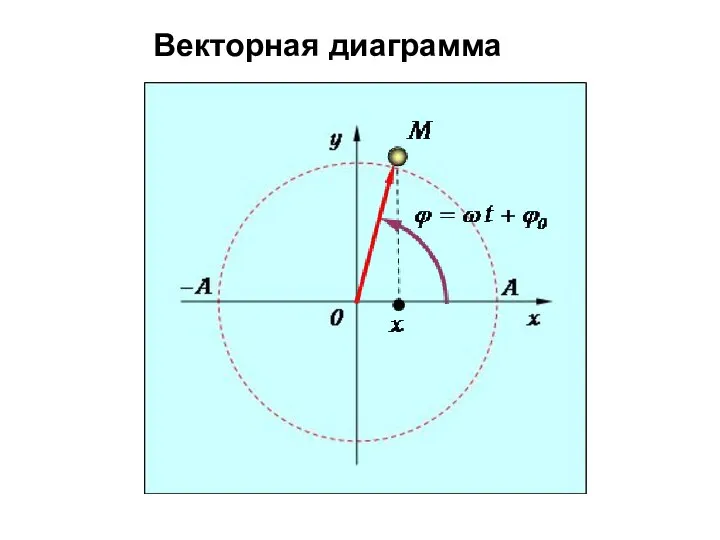
Векторная диаграмма

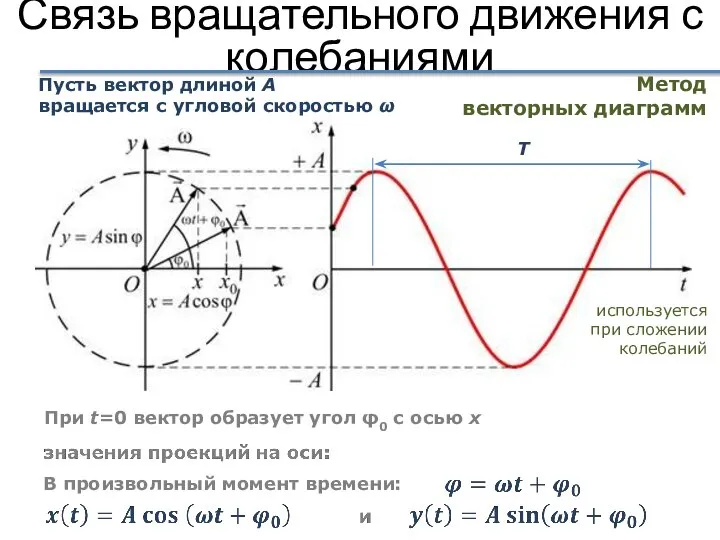
Связь вращательного движения с колебаниями
Пусть вектор длиной А
вращается с угловой скоростью ω
При t=0 вектор образует угол φ0 с осью х
В произвольный момент времени:
А
O
x
y
Метод
векторных диаграмм
используется при сложении колебаний

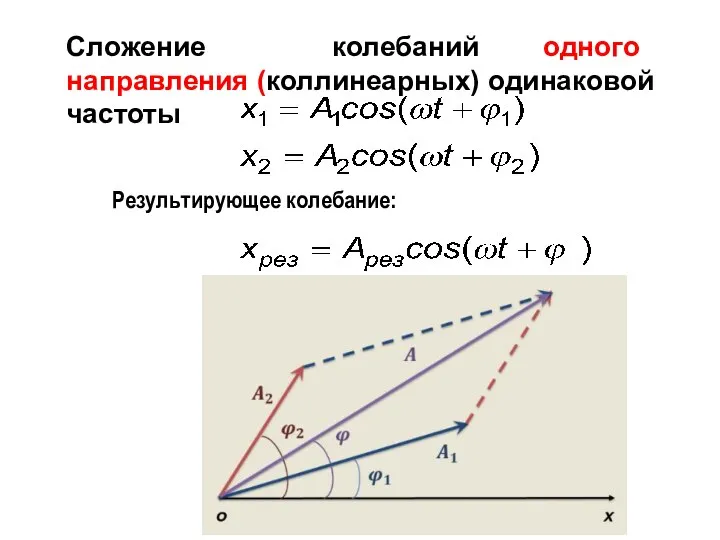
Сложение колебаний одного направления (коллинеарных) одинаковой частоты
Результирующее колебание:

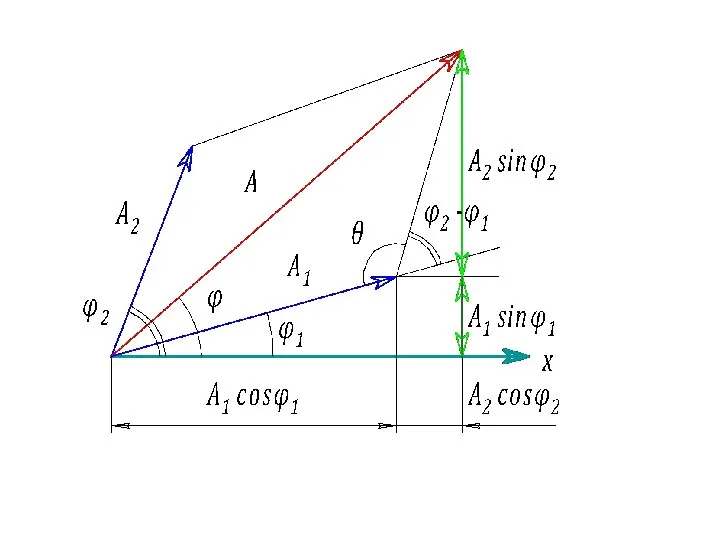
Сложение колебаний
Сложение колебаний одинакового направления
удобно проводить
с помощью
метода
векторных диаграмм
Амплитуда
1.
Начальная фаза
Результирующее колебание:
при
при
система с ОДНОЙ степенью свободы

Сложение колебаний в одной фазе
Колебания одинакового направления
1.
т.е.
Амплитуда
Условие МАКСИМУМА
Колебания усиливают друг друга
Четное количество
(коллинеарные)

Сложение колебаний в противофазе
Колебания одинакового направления
т.е.
Амплитуда
Условие МИНИМУМА
Колебания ослабляют друг друга
НЕчетное количество
при
колебания «гасят» друг друга
2.
(коллинеарные)

Сложение колебаний
Частоты складываемых колебаний мало отличаются
Результирующее колебание:
биения
Частота биений
можно рассматривать как
гармоническое колебание частоты ω,
амплитуда которого медленно изменяется по некоторому периодическому закону (пульсирует)
т.к.
то
3.
Колебания одинакового направления (Система с ОДНОЙ степенью свободы)
(коллинеарные)

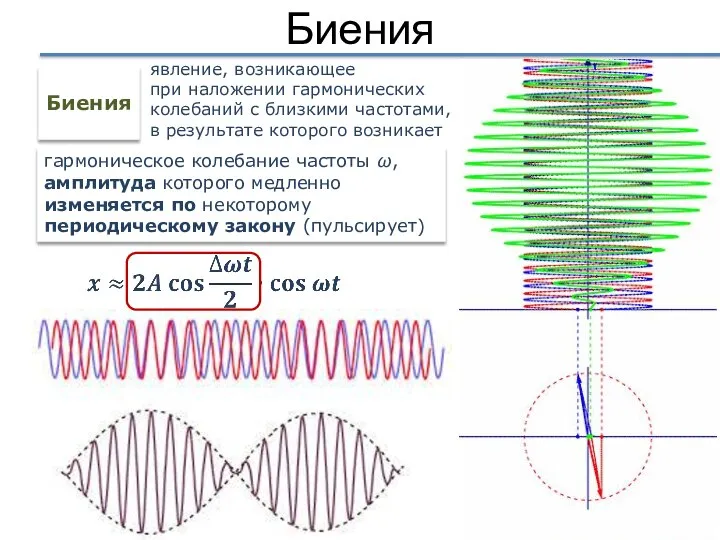
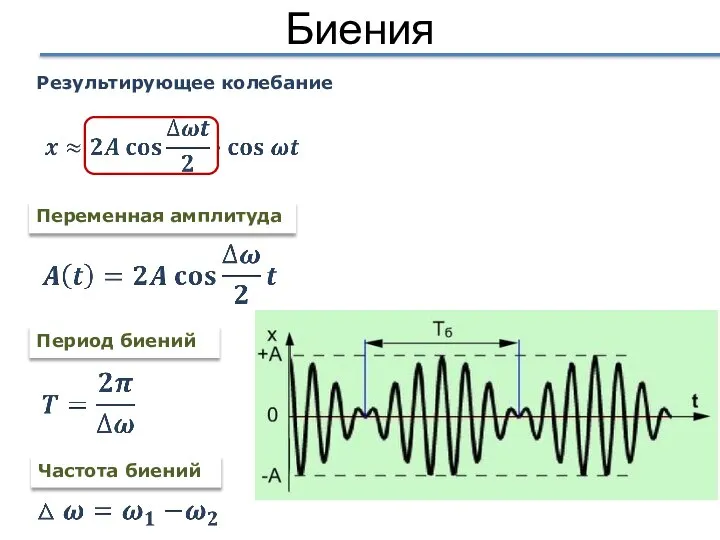
Биения
Биения
гармоническое колебание частоты ω,
амплитуда которого медленно изменяется по некоторому периодическому закону (пульсирует)
явление, возникающее
при наложении гармонических колебаний с близкими частотами,
в результате которого возникает

Биения
Частота биений
Переменная амплитуда
Период биений
Результирующее колебание

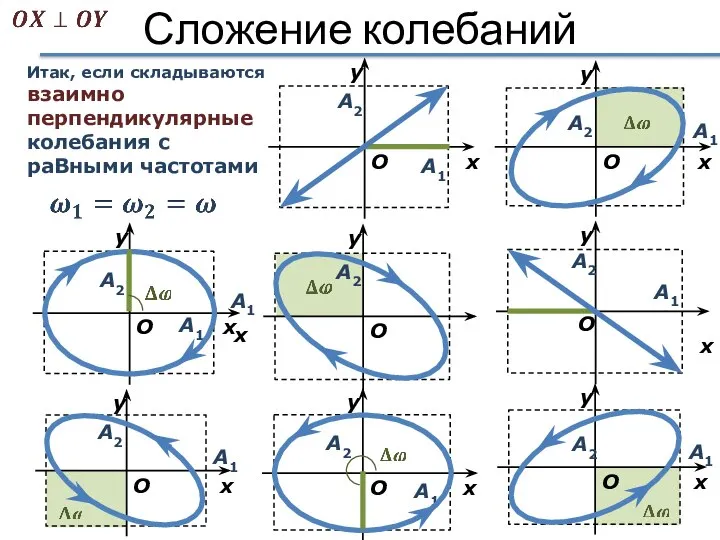
Сложение колебаний
Взаимно перпендикулярные колебания
Результирующее колебание:
в общем случае, точка будет совершать
периодические движения по эллиптической траектории
направление движения вдоль траектории и ориентация эллипса относительно осей зависят от разности фаз
Система с ДВУМЯ степенями свободы
Смещения малые
(выполняется закон Гука)
Частоты равны
Вдоль осей
ОХ и ОУ
(ортогональные)

Сложение колебаний
А1
x
Итак, если складываются
взаимно перпендикулярные колебания с раВными частотами

Сложение ортогональных колебаний.
Фигуры Лиссажу

Сложение колебаний: Фигуры Лиссажу
Если частоты не кратны, то
траектории движения – НЕзамкнутые кривые
отношение частот равно отношению числа точек касания фигуры
сторон прямоугольника,
в который она списана