Содержание
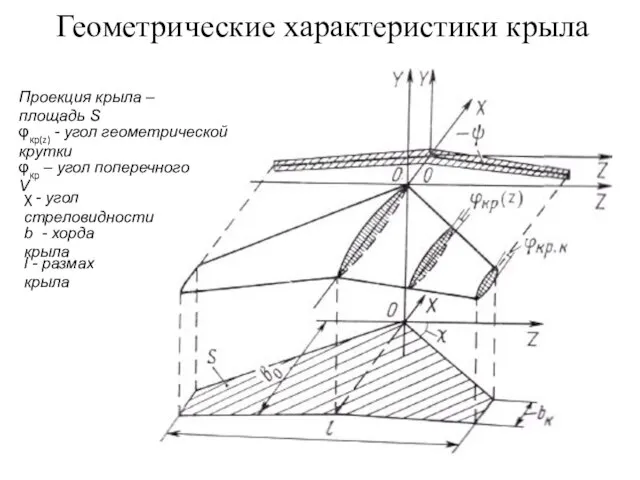
- 2. Геометрические характеристики крыла Проекция крыла – площадь S φкр(z) - угол геометрической крутки φкр – угол
- 3. Характеристики крыла Удлинение λ = l2/S - равное отношению квадрата размаха крыла к площади крыла. Степень
- 4. Образование вихревой пелены за крылом конечного размаха
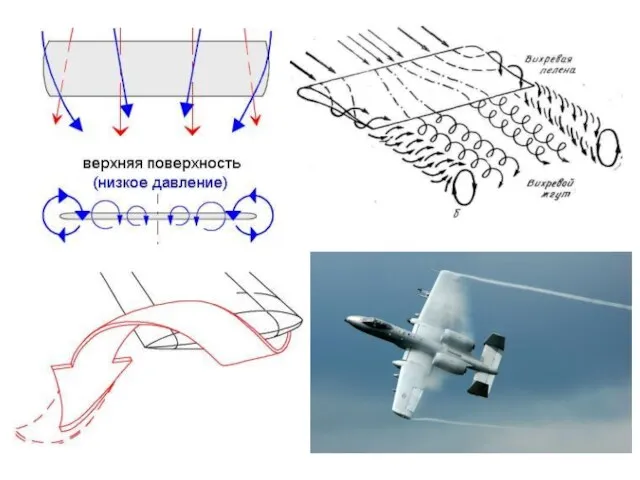
- 5. Концевой вихрь
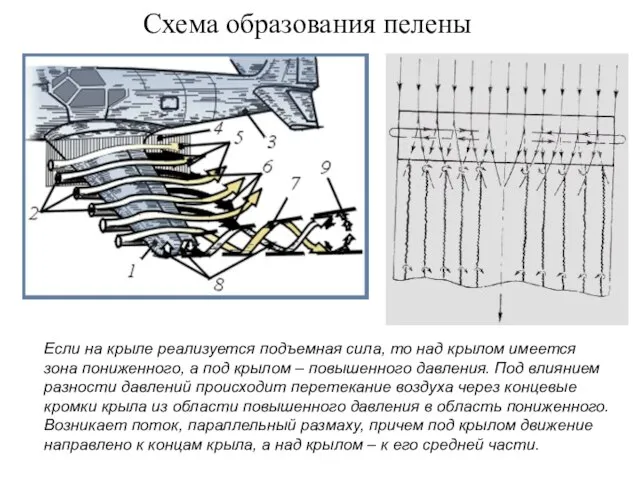
- 7. Схема образования пелены Если на крыле реализуется подъемная сила, то над крылом имеется зона пониженного, а
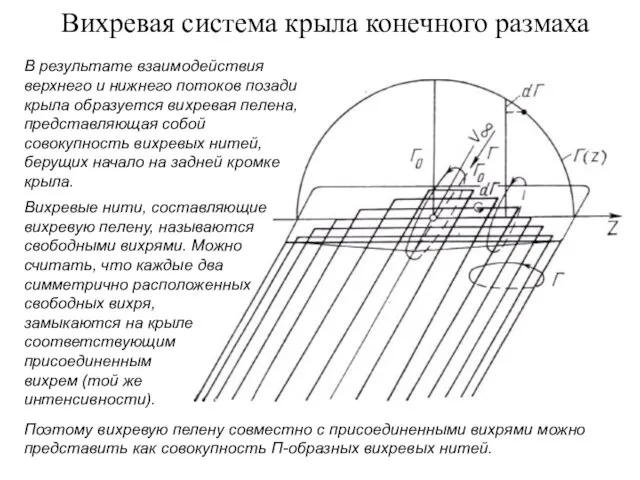
- 8. Вихревая система крыла конечного размаха В результате взаимодействия верхнего и нижнего потоков позади крыла образуется вихревая
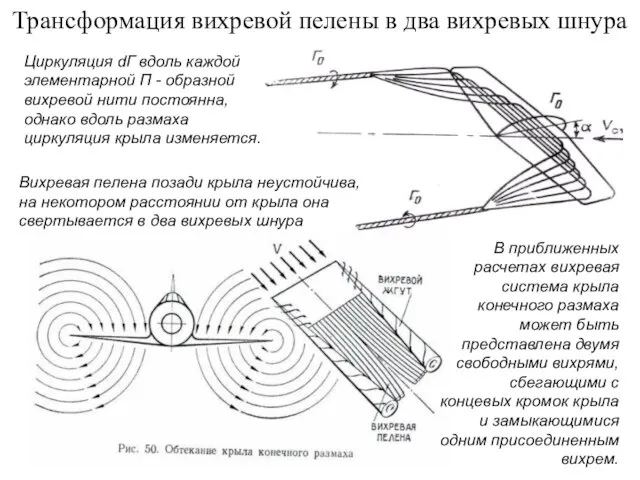
- 9. Трансформация вихревой пелены в два вихревых шнура В приближенных расчетах вихревая система крыла конечного размаха может
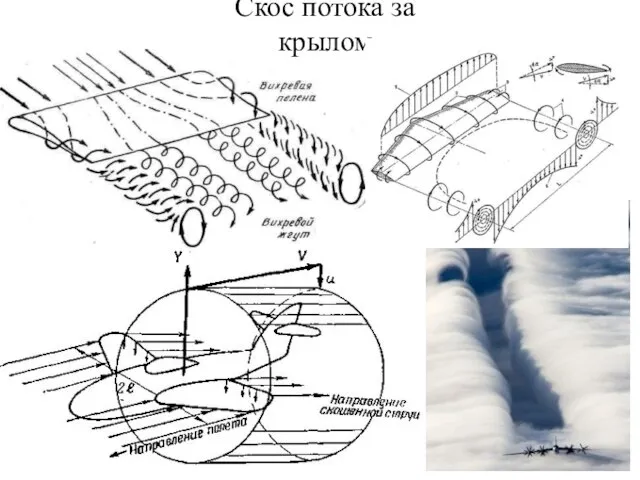
- 11. Скос потока за крылом
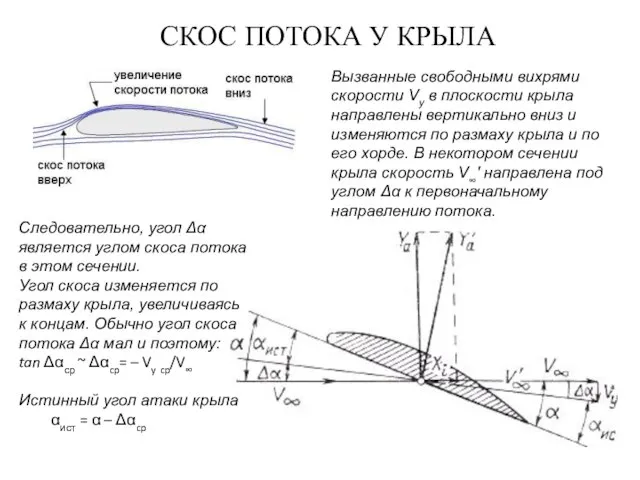
- 12. СКОС ПОТОКА У КРЫЛА Следовательно, угол Δα является углом скоса потока в этом сечении. Угол скоса
- 13. Скос потока
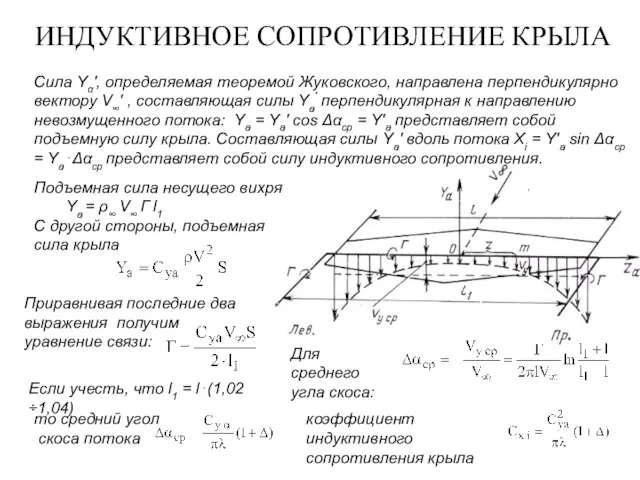
- 14. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ КРЫЛА Сила Υα', определяемая теоремой Жуковского, направлена перпендикулярно вектору V∞' , cоставляющая силы Ya'
- 15. Выводы 1. Величина индуктивного сопротивления тем больше, чем больше коэффициент Сyа и изменяется в зависимости от
- 16. Методы борьбы с образованием концевого вихря
- 20. Скачать презентацию









 Упругие колебания стержня с закрепленным концом
Упругие колебания стержня с закрепленным концом Построение эскизных компоновок редукторов
Построение эскизных компоновок редукторов Рубка металла
Рубка металла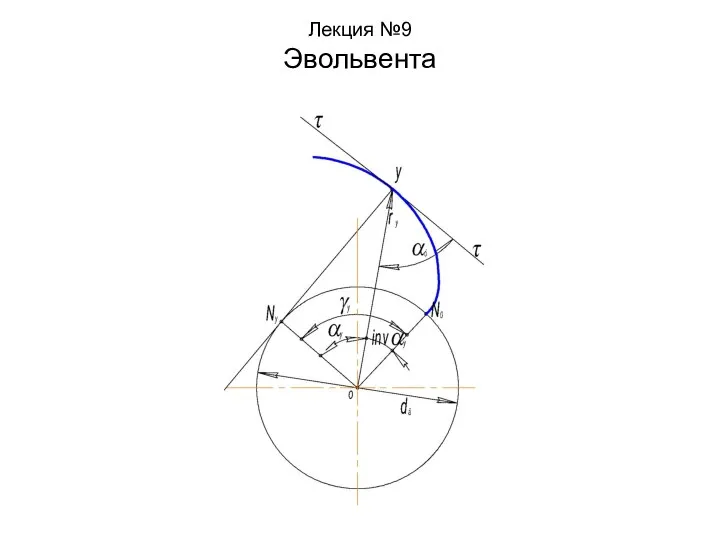 Эвольвента. Лекции 9
Эвольвента. Лекции 9 Вечный двигатель в истории
Вечный двигатель в истории IRS-P6 - усовершенствованный спутник дистанционного зондирования
IRS-P6 - усовершенствованный спутник дистанционного зондирования Сила трения
Сила трения Оптические приборы
Оптические приборы Электрические цепи постоянного тока
Электрические цепи постоянного тока Общий вид стационарной ЭТЛ
Общий вид стационарной ЭТЛ Электрическое поле в проводах и диэлектриках
Электрическое поле в проводах и диэлектриках Молния
Молния Электрические цепи переменного тока. Практическое занятие №1
Электрические цепи переменного тока. Практическое занятие №1 Игра-путешествие Физика – это интересно!
Игра-путешествие Физика – это интересно! Урок 22 Відбивання світла
Урок 22 Відбивання світла Механическая работа. Единицы работы. 7 класс
Механическая работа. Единицы работы. 7 класс Высокая пластичность
Высокая пластичность Теория ядерных реакторов. Семинар к курсовому проекту по спецкурсу № 2
Теория ядерных реакторов. Семинар к курсовому проекту по спецкурсу № 2 Лазер - история
Лазер - история Работа газа и пара при расширении. Двигатели внутреннего сгорания
Работа газа и пара при расширении. Двигатели внутреннего сгорания Физика – это наука о природе!
Физика – это наука о природе! Токи в различных средах
Токи в различных средах Работа сил тяжести и упругости. Потенциальная энергия
Работа сил тяжести и упругости. Потенциальная энергия Идеальный газ в МКТ
Идеальный газ в МКТ Презентация на тему Плотность вещества
Презентация на тему Плотность вещества  Определение проницаемости
Определение проницаемости Контрольная работа по теме МКТ
Контрольная работа по теме МКТ Презентация на тему Гидростатическое давление
Презентация на тему Гидростатическое давление