Содержание
- 2. ВВЕДЕНИЕ 3 1 КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА 4 2 ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ 5 2.2. ВЕКТОРЫ 5
- 3. Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач,
- 4. Интерес к векторам и векторному исчислению пробудился у математиков в XIX веке в связи с потребностями
- 5. 2.2. ВЕКТОРЫ Вектор-это отрезок, для которого указано, какой из его концов считается началом, а какой –
- 6. ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ Рисунок 2 - Изображение правила треугольника Рисунок 3 - Изображение правила параллелограмма
- 7. Если через некоторую точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление
- 8. 4.2 Доказательство некоторых теорем Пусть точки А, В, С и Р такие, что ОР=mOA+nOB+рОС (OА, ОС
- 9. 4.3 Нахождение расстояний и углов На рёбрах DA,DB,AC тетраэдра DABC взяты соответственно точки L, N, F
- 10. 5.2 Задачи на построения Вершина В прямоугольного параллелепипеда АВСDA1B1C1D1 с отношением рёбер AB:DA:AA1=1:2:3 принята за начало
- 11. Аналогично если плоскость α пересекает ось Ву в точке L, то точка L имеет координаты (0;l;0).
- 12. 5.3 Задачи на вычисления расстояний и углов В основании пирамиды МАВС лежит равнобедренный треугольник с прямым
- 13. векторов ВС и ВМ. Получаем B(-1;0;0;), K(-1/2;0;1/2), AK(-3/2;0;1/2), BC(1;1;0), BM (1;0;1). Если вектор n(k;l;m) перпендикулярен плоскости
- 14. Обобщая вышеизложенные доводы, мы удостоверились, что использование векторно-координатного метода позволяет с лёгкостью решать множество задач самых
- 16. Скачать презентацию
Слайд 2ВВЕДЕНИЕ 3
1 КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА 4
2 ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ 5
2.2. ВЕКТОРЫ
ВВЕДЕНИЕ 3
1 КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА 4
2 ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ 5
2.2. ВЕКТОРЫ

3 КООРДИНАТЫ 7
4 РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ И СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 8
4.2 ДОКАЗАТЕЛЬСТВО НЕКОТОРЫХ ТЕОРЕМ 8
4.3 НАХОЖДЕНИЕ РАССТОЯНИЙ И УГЛОВ 9
5 РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ 10
5.2 ЗАДАЧИ НА ПОСТРОЕНИЯ 10
5.3 ЗАДАЧИ НА ВЫЧИСЛЕНИЯ РАССТОЯНИЙ И УГЛОВ 12
ЗАКЛЮЧЕНИЕ 14
СПИСОК ЛИТЕРАТУРЫ 15
Содержание
Слайд 3Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения,
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения,

«Векторный» путь построения геометрии предложил в 1918 году известный немецкий математик Герман Вейль. Векторы можно использовать как для решения планиметрических задач, так и для стереометрических.
Векторно-координатный метод решения задач позволяет с лёгкостью решать даже самые большие и сложные задачи, избегать долгих доказательств теорем. С помощью векторов можно вычислять расстояния и углы, доказывать теоремы, строить перпендикулярные и параллельные прямые и отрезки, строить сечения, доказывать равенство геометрических фигур и многое другое.
В настоящее время векторно-координатный метод используется в алгебре, геометрии, физике, механике; понятие векторного пространства используется в теории вероятностей, математической экономике, биологии, лингвистике и т.д.
3
ВВЕДЕНИЕ
Слайд 4Интерес к векторам и векторному исчислению пробудился у математиков в XIX веке
Интерес к векторам и векторному исчислению пробудился у математиков в XIX веке

Термин «вектор» происходит от латинского слова vector, что означает несущий или ведущий, влекущий, переносящий
В современной математике раздел, в котором излагается учение о действиях над векторами, называют векторной алгеброй, так как эти действия имеют много общих свойств с алгебраическими действиями. 4
КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА
Слайд 52.2. ВЕКТОРЫ
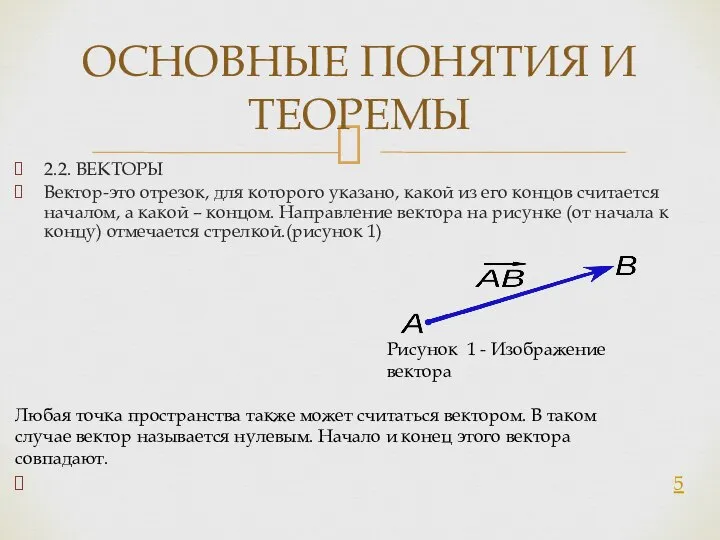
Вектор-это отрезок, для которого указано, какой из его концов считается
2.2. ВЕКТОРЫ
Вектор-это отрезок, для которого указано, какой из его концов считается
5
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Рисунок 1 - Изображение вектора
Любая точка пространства также может считаться вектором. В таком случае вектор называется нулевым. Начало и конец этого вектора совпадают.
Слайд 6ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Рисунок 2 - Изображение правила треугольника
Рисунок 3 - Изображение
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Рисунок 2 - Изображение правила треугольника
Рисунок 3 - Изображение
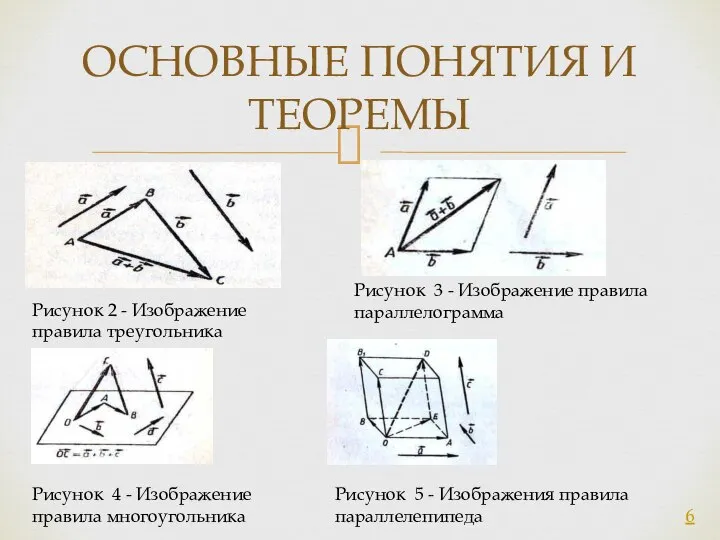
Рисунок 4 - Изображение правила многоугольника
Рисунок 5 - Изображения правила параллелепипеда 6
Слайд 7Если через некоторую точку пространства проведены три попарно перпендикулярные прямые, на каждой
Если через некоторую точку пространства проведены три попарно перпендикулярные прямые, на каждой

7
КООРДИНАТЫ
Слайд 84.2 Доказательство некоторых теорем
Пусть точки А, В, С и Р такие, что ОР=mOA+nOB+рОС
4.2 Доказательство некоторых теорем
Пусть точки А, В, С и Р такие, что ОР=mOA+nOB+рОС

8
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ
Пусть точки А, В, С и Р лежат в одной плоскости, тогда векторы
АР=ОР-ОА, АВ=ОВ-ОА, АС=ОС-ОА будут линейно зависимыми, следовательно
ОР-ОА=n(OB-OA)+p(OC-OA),
OP=(1- n- p)OA+nOB+pOC. И в силу единственности разложения вектора OP по векторам ОА, ОВ, ОС получим
m=1- n –p или m+ n+ p=1
Доказательство достаточности:
Пусть m+n+p=1, тогда
OP-OA=mOA+nOB+pOC-OA=mOA+nOB+pOC-(m+n+p)*OA=n(OB-OA)+p(OC-OA)
Отсюда АР=nAB+pAС и по определению P принадлежит плоскости АВС.
Рисунок 7 - Изображение фигуры
Слайд 94.3 Нахождение расстояний и углов
На рёбрах DA,DB,AC тетраэдра DABC взяты соответственно точки L,
4.3 Нахождение расстояний и углов
На рёбрах DA,DB,AC тетраэдра DABC взяты соответственно точки L,

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ
Решение:
Пусть М – точка пересечения рассматриваемой плоскости с ребром BC и
DA=a, DB=b, DC=c.
Так как точки M,N,L,F лежат в одной плоскости, причём последние три точки не лежат на одной прямой, то по формуле
DM=kDL+lDN+(1 – k – l)DF=ka/2+lb/3+(1 – k – l)(3/4a+1/4c).
С другой стороны, по формуле (1)
DM=(1-m)b+mc
где m – отношение ВМ:ВС. Так как векторы а,b,с не компланарны, то на основании утверждения о разложении вектора по трём некомпланарным, мы получим систему:
k/2+(1 – k – l)3/4=0, l/3=1 – m,
(1 – k – l)1/4=m. 9
Отсюда m=2/5 и ВМ:МС=2/3.
Рисунок 8 - Изображение фигуры
Слайд 105.2 Задачи на построения
Вершина В прямоугольного параллелепипеда АВСDA1B1C1D1 с отношением рёбер AB:DA:AA1=1:2:3 принята
5.2 Задачи на построения
Вершина В прямоугольного параллелепипеда АВСDA1B1C1D1 с отношением рёбер AB:DA:AA1=1:2:3 принята

векторы ВА, 1/2ВС и 1/3ВВ1 приняты соответственно за единичные векторы i, j, k.
Построить сечение параллелепипеда плоскостью α , заданной в этой системе координат уравнением 4x + y - 2z - 2=0. (рис 9)
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Рисунок 9 - Изображение фигуры
Для построения данного сечения найдём три точки, принадлежащие плоскости α, но не лежащие на одной прямой, например, точки пересечения плоскости α с осями координат. Так, если плоскость α пересекает ось Вх в точке К, то точка К имеет координаты (к;0;0). Подставляя эти координаты в уравнение плоскости α ,получим к=1/2. Таким образом, плоскость α пересекает ось Вх в точке К(1/2;0;0). Построим эту точку.
10
Слайд 11Аналогично если плоскость α пересекает ось Ву в точке L, то точка
Аналогично если плоскость α пересекает ось Ву в точке L, то точка

Точно так же находим, что плоскость α пересекает ось Вz в точке М(0;0;-построим эту точку и затем построим сечение призмы плоскостью α, проходящей через точки К,L,M. Получаем четырёхугольник КСD2A2.
11
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Слайд 125.3 Задачи на вычисления расстояний и углов
В основании пирамиды МАВС лежит равнобедренный треугольник
5.3 Задачи на вычисления расстояний и углов
В основании пирамиды МАВС лежит равнобедренный треугольник

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Установив, что медианно МО грани МАВ является высотой пирамиды, т.е. МО┴АВ и МО┴ОС, и что ОА =ОС=ОМ, зададим в пространстве прямоугольную систему координат Охуz, как показано на рисунке.
OA=i ; OC=j ; OM=k
В этой системе координат O(0;0;0), A(1;0;0), C(0;1;0), M(0,0,1)
Находим далее координаты точек В и К, вектора АК, коллинеарного прямой АК, и
12
Слайд 13векторов ВС и ВМ. Получаем B(-1;0;0;), K(-1/2;0;1/2), AK(-3/2;0;1/2), BC(1;1;0), BM (1;0;1).
Если
векторов ВС и ВМ. Получаем B(-1;0;0;), K(-1/2;0;1/2), AK(-3/2;0;1/2), BC(1;1;0), BM (1;0;1).
Если

k*1+l*1+m*0=0
k*1+l*0+m*1=0
откуда, полагая, например, что k=1, находим, что l=-1, m=-1, т.е. n(1;-1;-1).
Пусть φ – это искомый угол. Тогда
13
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
Рисунок 11 - продолжение решения задачи
Таким образом, угол между прямой АК и плоскостью МВС равен arcsin (2√30)/15 Содержание
Слайд 14Обобщая вышеизложенные доводы, мы удостоверились, что использование векторно-координатного метода позволяет с лёгкостью
Обобщая вышеизложенные доводы, мы удостоверились, что использование векторно-координатного метода позволяет с лёгкостью

14
ЗАКЛЮЧЕНИЕ
 Диполь. Поле системы зарядов. Теорема Ирншоу
Диполь. Поле системы зарядов. Теорема Ирншоу Принцип Гюйгенса. Закон отражения света. Плоские и сферические зеркала. Закон преломления света. Полное внутреннее отражение
Принцип Гюйгенса. Закон отражения света. Плоские и сферические зеркала. Закон преломления света. Полное внутреннее отражение Рефрактометрия. Преломление света
Рефрактометрия. Преломление света Порядок заправки верхней и нижней нити
Порядок заправки верхней и нижней нити Физика и познание мира
Физика и познание мира Цепь переменного тока с индуктивностью
Цепь переменного тока с индуктивностью Устройство электроскопа
Устройство электроскопа Основные физические явления, используемые в работе ТСО. Тема 3
Основные физические явления, используемые в работе ТСО. Тема 3 Дефектация деталей
Дефектация деталей Электромагнитная индукция
Электромагнитная индукция Электронные средства обучения
Электронные средства обучения Закон инерции. Инерциальная система отсчёта. Первый закон Ньютона. Сила. Измерение сил
Закон инерции. Инерциальная система отсчёта. Первый закон Ньютона. Сила. Измерение сил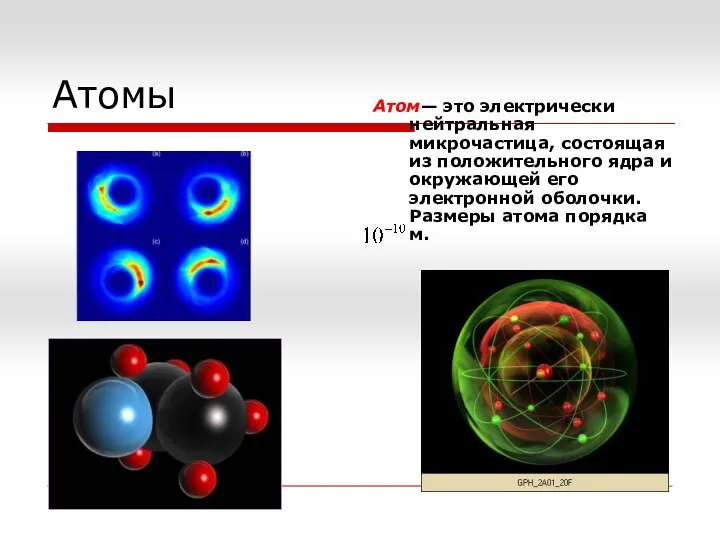 Атомы
Атомы Микроскоп
Микроскоп 13. СВЕТОТЕХНИКА 2020
13. СВЕТОТЕХНИКА 2020 Луиджи Гальвани и Алессандро Вольта. Тема № 5
Луиджи Гальвани и Алессандро Вольта. Тема № 5 Плакаты по физике
Плакаты по физике Солитоны
Солитоны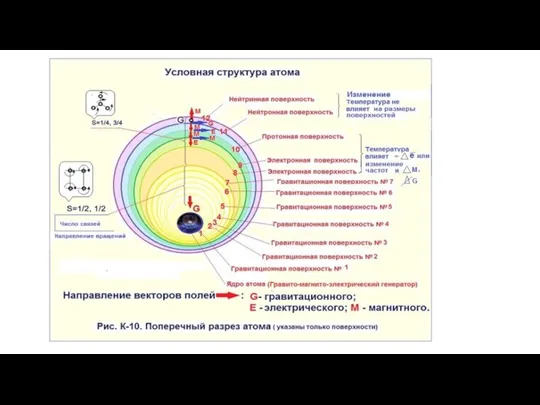 Условная структура атома
Условная структура атома Генератор электрического тока
Генератор электрического тока Механические колебания
Механические колебания Экологическое воспитание на внеурочных занятиях по физике
Экологическое воспитание на внеурочных занятиях по физике Оптимизация программы для определения частоты аудиосигнала
Оптимизация программы для определения частоты аудиосигнала Механическая работа. Энергия
Механическая работа. Энергия Внутренняя энергия
Внутренняя энергия Явления тяготения. Сила тяжести
Явления тяготения. Сила тяжести Электромагнитные колебания и волны
Электромагнитные колебания и волны Из истории открытия закона всемирного тяготения…
Из истории открытия закона всемирного тяготения…