Магнитостатическое поле в вакууме. Часть 3

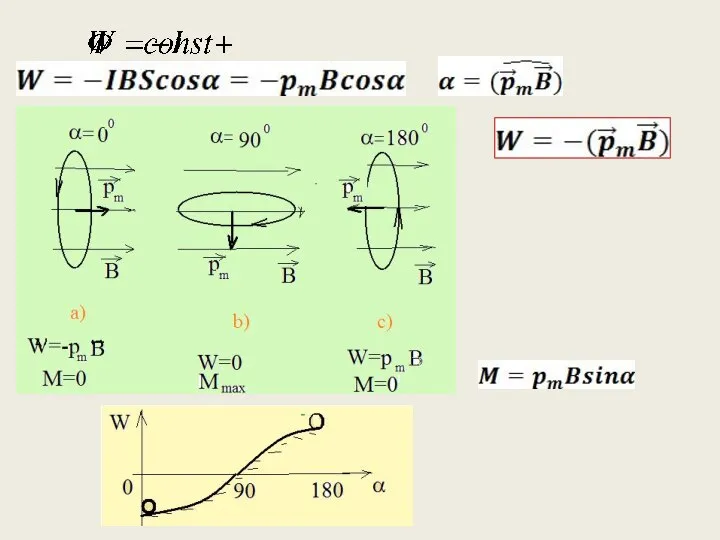
Потенциальная энергия контура с током
в магнитном поле
Работа по перемещению контура (проводника) с постоянным током в постоянном магнитном поле не зависит от формы перемещения контура, а определяется только начальным и конечным положениями контура в магнитном поле. В таком поле можно ввести понятие потенциальной энергии.
Величина механической работы определяется убылью потенциальной энергии контура с током в постоянном магнитном поле.
Работа сил поля по перемещению контура с постоянным током в магнитостатическом поле:

Положение контура
соответствует минимуму его потенциальной энергии, т.е. состоянию устойчивого равновесия.

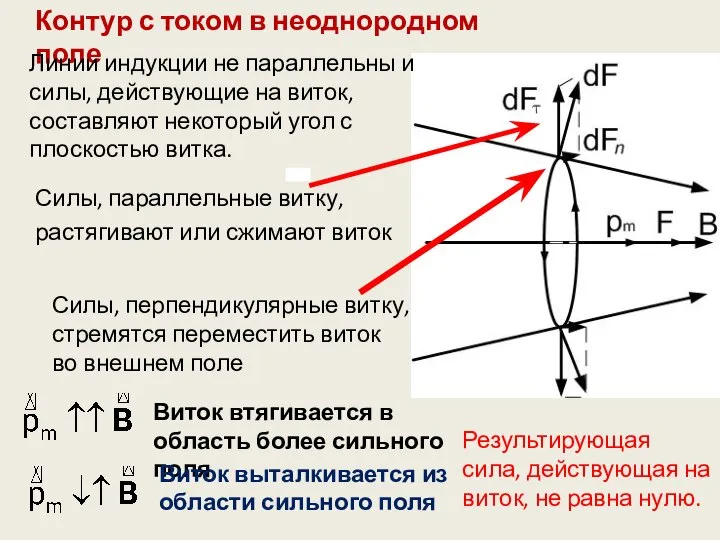
Контур с током в неоднородном поле
Линии индукции не параллельны и силы, действующие на виток, составляют некоторый угол с плоскостью витка.
Силы, параллельные витку,
растягивают или сжимают виток
Силы, перпендикулярные витку, стремятся переместить виток во внешнем поле
Виток втягивается в область более сильного поля
Виток выталкивается из области сильного поля
Результирующая сила, действующая на виток, не равна нулю.

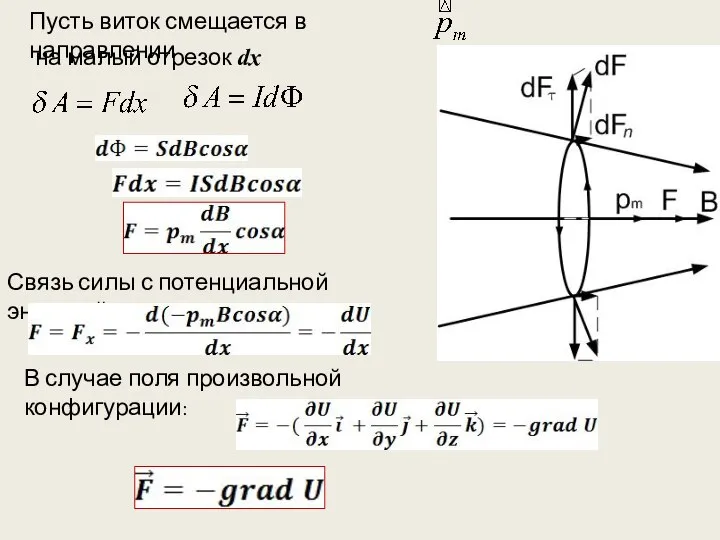
Пусть виток смещается в направлении
на малый отрезок dx
Связь силы с потенциальной энергией:
В случае поля произвольной конфигурации:

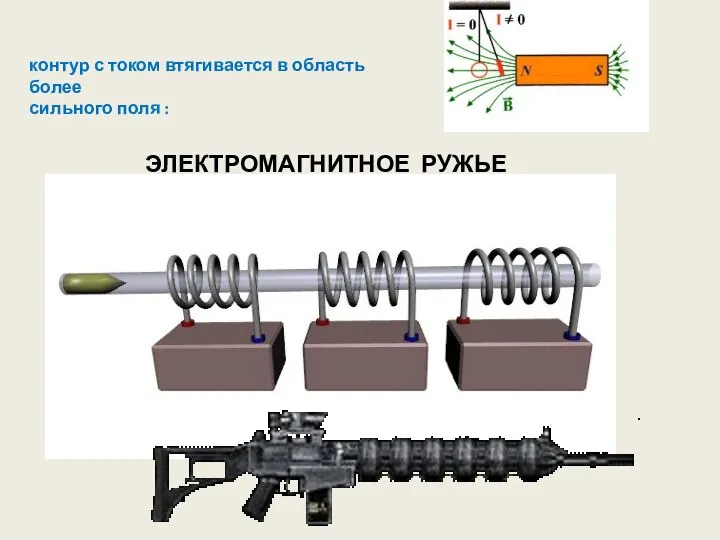
ЭЛЕКТРОМАГНИТНОЕ РУЖЬЕ
контур с током втягивается в область более
сильного поля :

Основные уравнения магнитостатического поля в вакууме
1. Теорема Гаусса для магнитного поля в вакууме
Линии магнитной индукции всегда замкнуты, т.е. не имеют ни начала, ни конца.
Отсутствие в природе магнитных зарядов приводит к тому, что для произвольной замкнутой поверхности, расположенной в магнитном поле, поток вектора сквозь нее всегда равен нулю.
-интегральная форма записи теоремы Гаусса.

2. Теорема о циркуляции вектора индукции магнитного поля.
Эксперимент:
Циркуляция вектора индукции магнитного поля в вакууме по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых данным контуром, умноженной на магнитную постоянную .

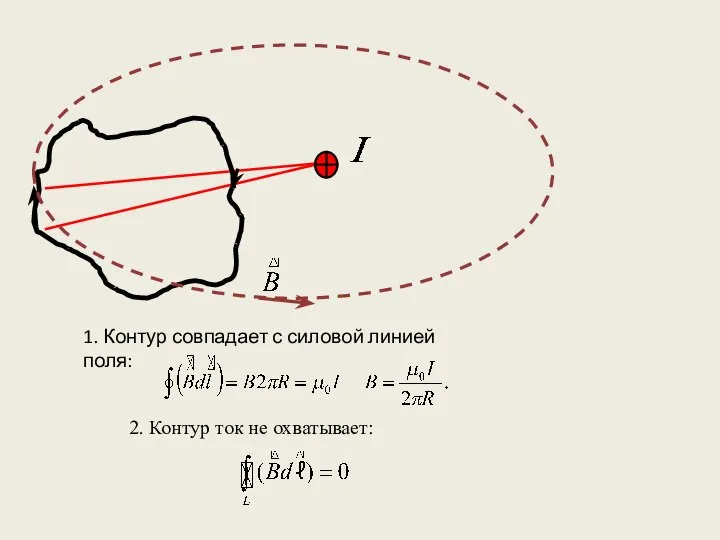
2. Контур ток не охватывает:
1. Контур совпадает с силовой линией поля:

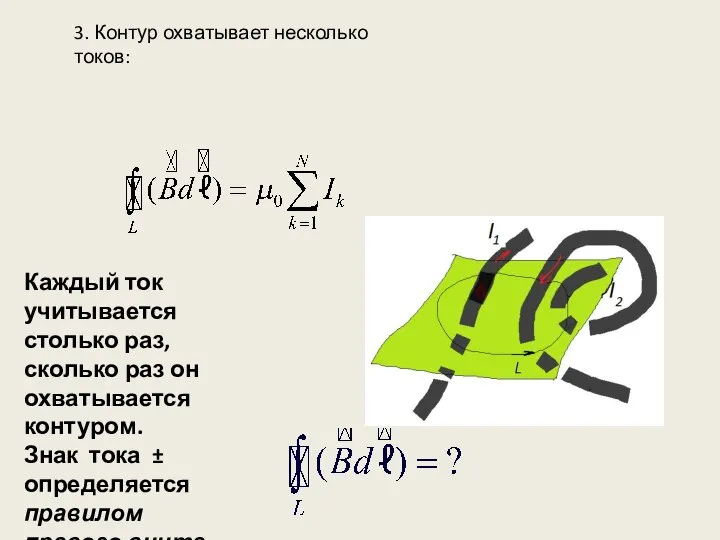
3. Контур охватывает несколько токов:
Каждый ток учитывается столько раз, сколько раз он охватывается контуром.
Знак тока ± определяется правилом правого винта.

Циркуляция вектора индукции магнитного поля в вакууме по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых данным контуром, умноженной на магнитную постоянную .
-интегральная форма записи теоремы о циркуляции вектора .
Отсюда следует, что источниками стационарного магнитного поля являются постоянные токи проводимости.

Справка из векторной алгебры: векторное поле, в котором циркуляция вектора по замкнутому контуру не равна нулю, является вихревым.
Стационарное магнитное поле является вихревым.

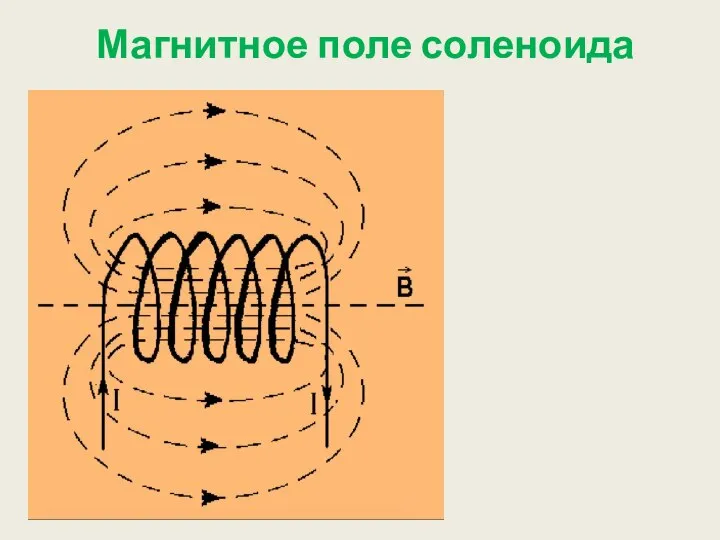
Магнитное поле соленоида

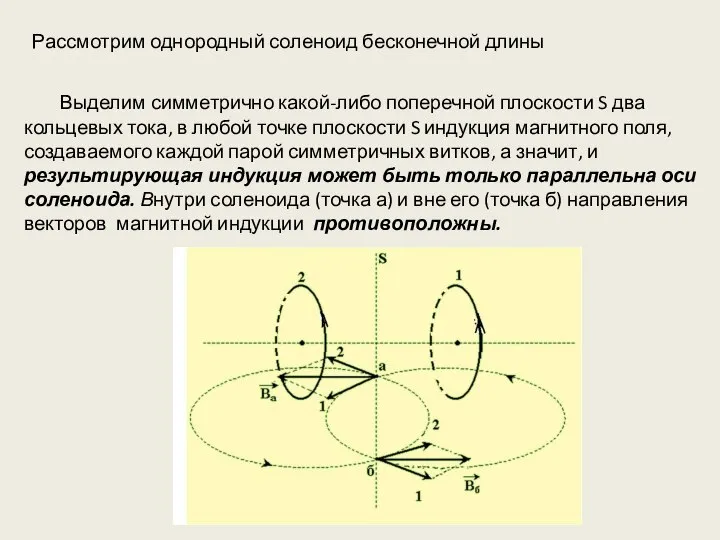
Выделим симметрично какой-либо поперечной плоскости S два кольцевых тока, в любой точке плоскости S индукция магнитного поля, создаваемого каждой парой симметричных витков, а значит, и результирующая индукция может быть только параллельна оси соленоида. Внутри соленоида (точка а) и вне его (точка б) направления векторов магнитной индукции противоположны.
Рассмотрим однородный соленоид бесконечной длины

Величина индукции магнитного поля внутри бесконечно длинного соленоида:
Магнитное поле бесконечного соленоида однородно и полностью сосредоточено в объеме соленоида.

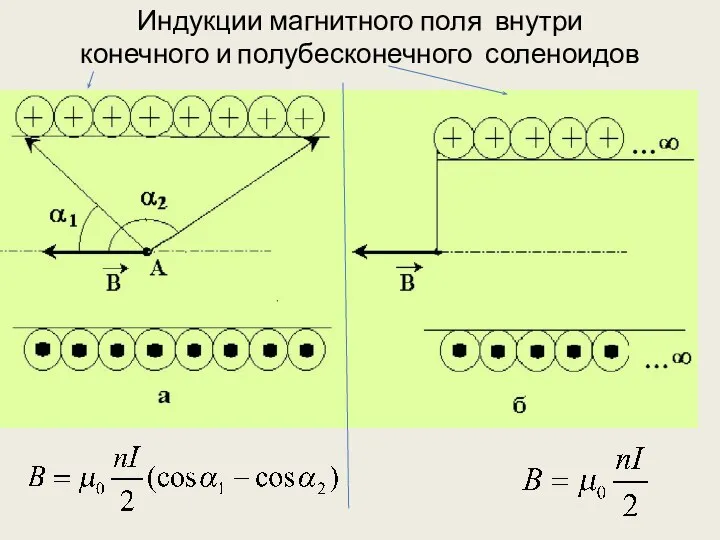
Индукции магнитного поля внутри
конечного и полубесконечного соленоидов

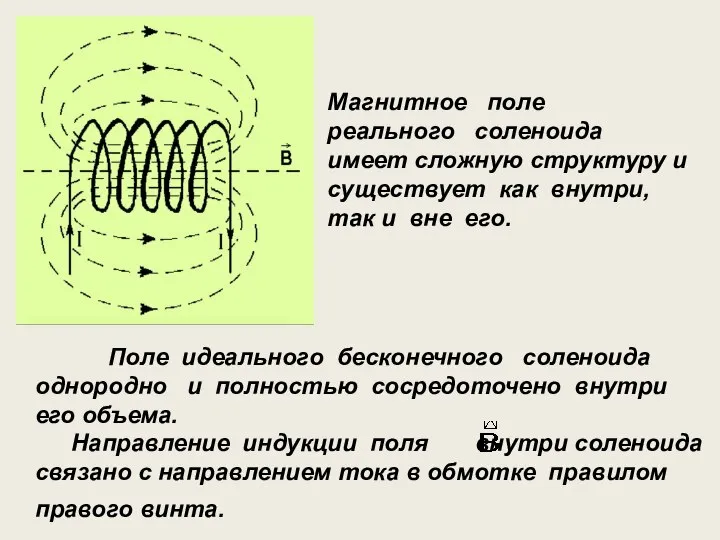
Поле идеального бесконечного соленоида однородно и полностью сосредоточено внутри его объема.
Направление индукции поля внутри соленоида связано с направлением тока в обмотке правилом правого винта.
Магнитное поле реального соленоида имеет сложную структуру и существует как внутри, так и вне его.

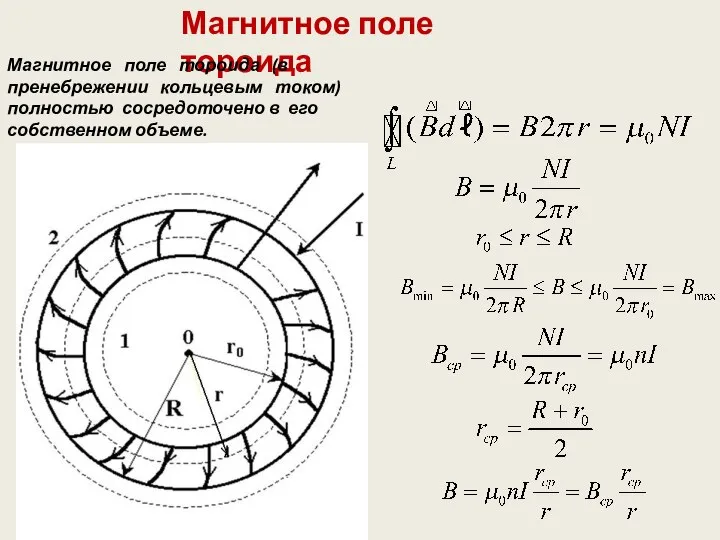
Магнитное поле тороида
Магнитное поле тороида (в пренебрежении кольцевым током) полностью сосредоточено в его собственном объеме.

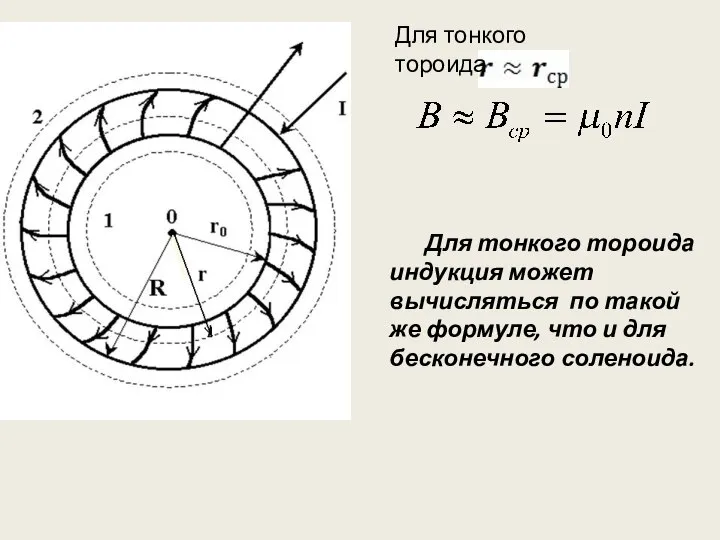
Для тонкого тороида индукция может вычисляться по такой же формуле, что и для бесконечного соленоида.
Для тонкого тороида