Содержание
- 2. Электрический заряд - это внутреннее свойство тел или частиц, характеризующее их способность к электромагнитным взаимодействиям. Единица
- 3. Фундаментальные свойства электрического заряда : положителен или отрицателен. Одноименные заряды отталкиваются, разноименные - притягиваются. инвариантен -
- 4. Закон сохранения электрического заряда Алгебраическая сумма электрических зарядов любой замкнутой системы остается неизменной, какие бы процессы
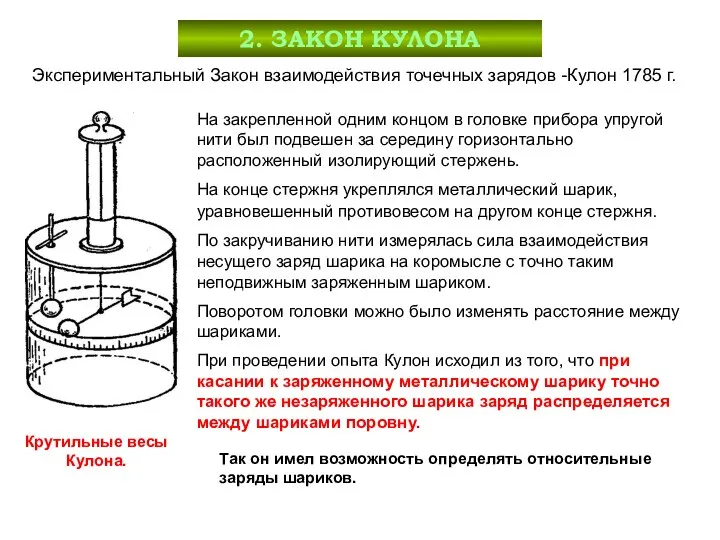
- 5. 2. ЗАКОН КУЛОНА На закрепленной одним концом в головке прибора упругой нити был подвешен за середину
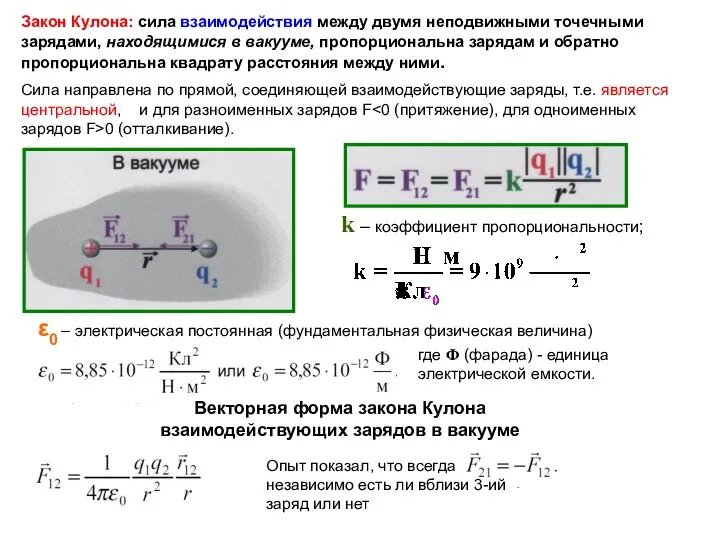
- 6. Закон Кулона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно
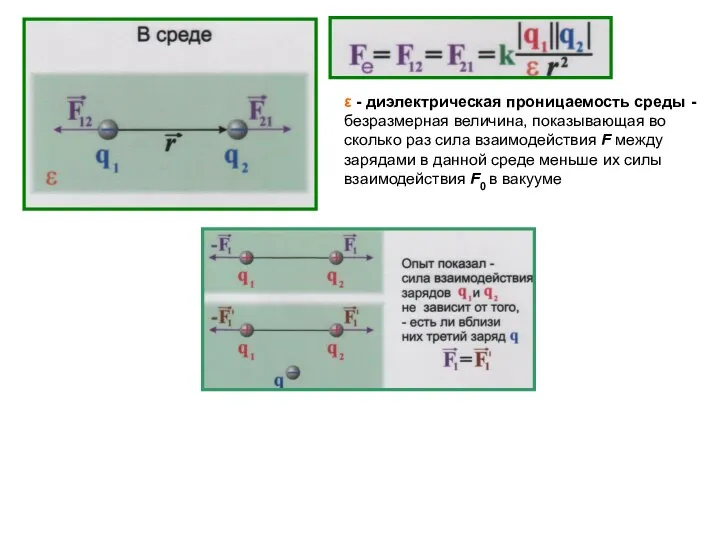
- 7. ε - диэлектрическая проницаемость среды - безразмерная величина, показывающая во сколько раз сила взаимодействия F между
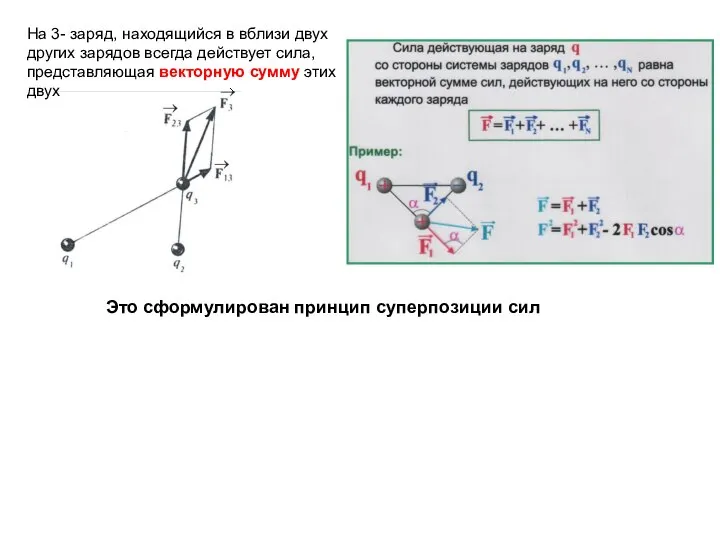
- 8. На 3- заряд, находящийся в вблизи двух других зарядов всегда действует сила, представляющая векторную сумму этих
- 9. Согласно современным представлениям: Взаимодействие неподвижных зарядов осуществляется электростатическим полем. Заряд возбуждает в окружающем его пространстве электрическое
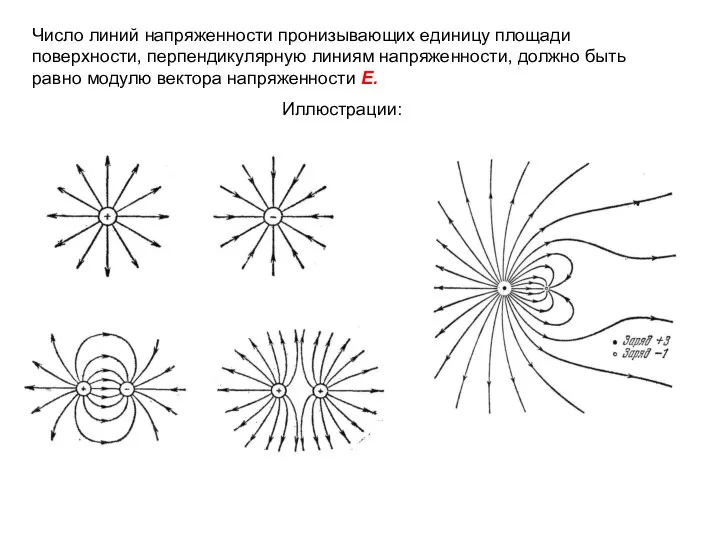
- 10. Они направлены по направлению вектора E, касательные к ним в каждой точке совпадают с направлением вектора
- 11. Число линий напряженности пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора напряженности
- 12. 4. Поток вектора напряженности Элементарным потоком вектора напряженности через элементарную площадку dS называется скалярная величина: Поток
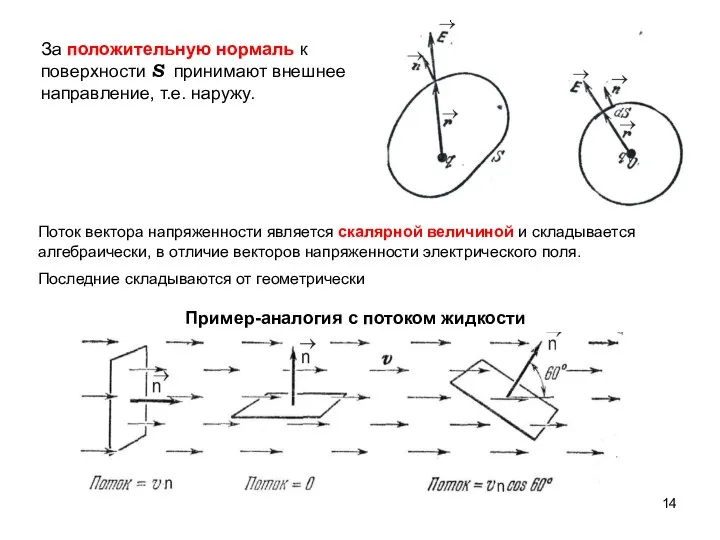
- 14. За положительную нормаль к поверхности S принимают внешнее направление, т.е. наружу. Поток вектора напряженности является скалярной
- 15. 5. Теорема Гаусса Эта теорема определяет поток вектора напряженности электрического поля через произвольную замкнутую поверхность. Случай
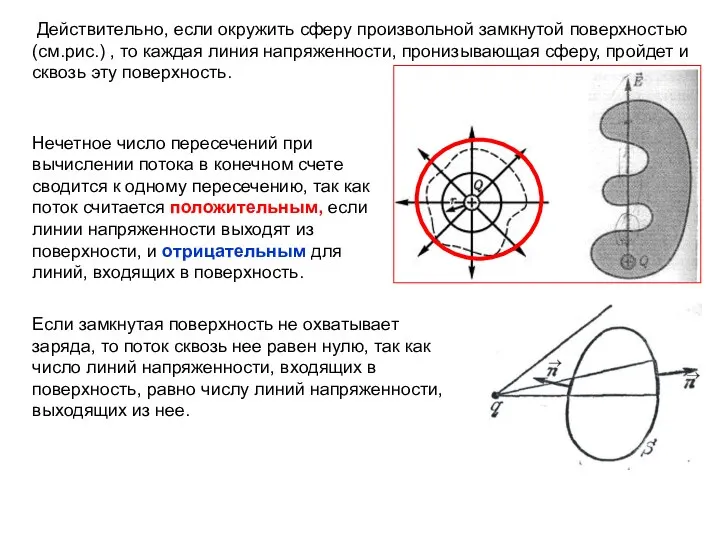
- 16. Действительно, если окружить сферу произвольной замкнутой поверхностью (см.рис.) , то каждая линия напряженности, пронизывающая сферу, пройдет
- 17. Теорема Гаусса для электростатического поля в вакууме, поток вектора напряженности электростатического поля в вакууме сквозь произвольную
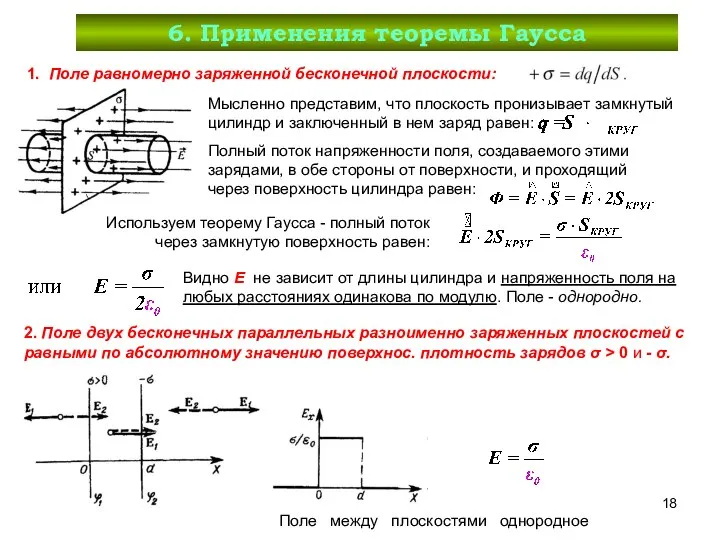
- 18. 6. Применения теоремы Гаусса 1. Поле равномерно заряженной бесконечной плоскости: Полный поток напряженности поля, создаваемого этими
- 20. Скачать презентацию









 Магнитные явления
Магнитные явления Электростатика. Диагностико-коррекционный тест. 8 класс
Электростатика. Диагностико-коррекционный тест. 8 класс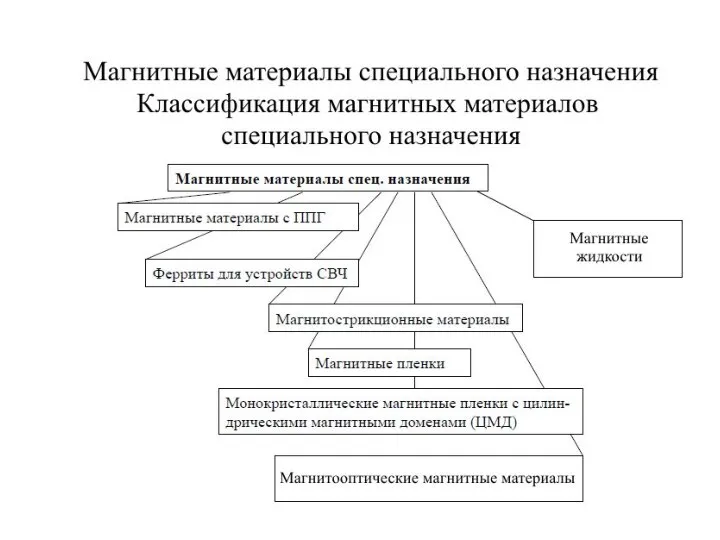 Магнитные материалы специального назначения. (Лекция 8)
Магнитные материалы специального назначения. (Лекция 8) Откуда берется радуга?
Откуда берется радуга? Пирометры
Пирометры Манометры поршневой жидкостный насос. Гидравлический пресс (7 класс)
Манометры поршневой жидкостный насос. Гидравлический пресс (7 класс) 8e84aba704c3488a88a3d72ef17c3ee4
8e84aba704c3488a88a3d72ef17c3ee4 Сообщающиеся сосуды (урок физики, 7 класс)
Сообщающиеся сосуды (урок физики, 7 класс) Производство и передача электроэнергии в РФ
Производство и передача электроэнергии в РФ Поколения ядерных реакторов. Лекция 6
Поколения ядерных реакторов. Лекция 6 Диэлектрики и проводники в электрическом поле
Диэлектрики и проводники в электрическом поле Слесарные операции
Слесарные операции Направляющие системы передачи электромагнитных сигналов связи
Направляющие системы передачи электромагнитных сигналов связи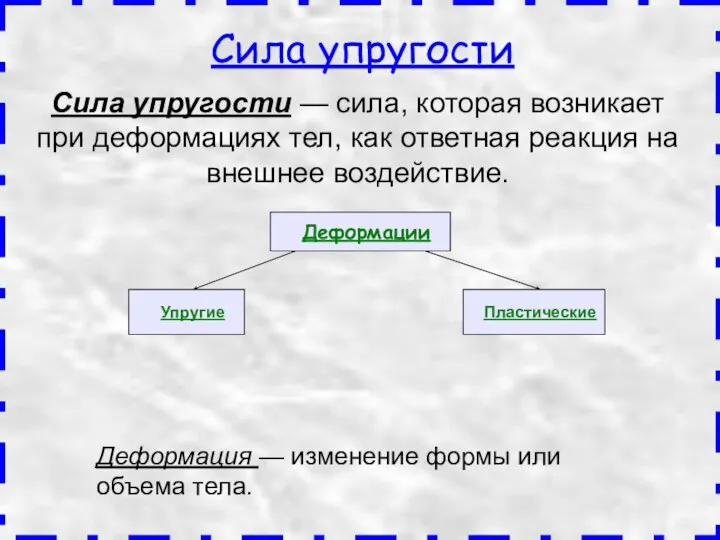 Силы в природе. Закон Гука
Силы в природе. Закон Гука Коробка передач
Коробка передач Атомное ядро. Дефект масс
Атомное ядро. Дефект масс Л3.7. Электротехнические материалы
Л3.7. Электротехнические материалы Презентация на тему Вакуумные приборы
Презентация на тему Вакуумные приборы  Электрический ток в жидкостях
Электрический ток в жидкостях Сверхпроводимость материалов
Сверхпроводимость материалов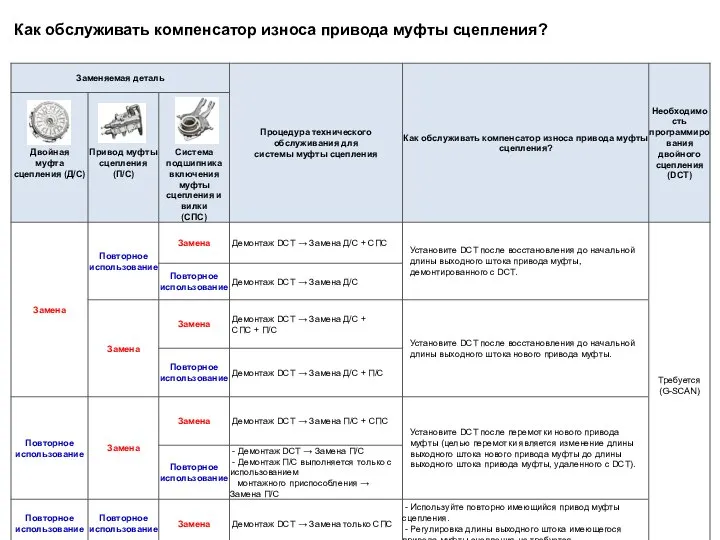 Как обслуживать компенсатор износа привода муфты сцепления
Как обслуживать компенсатор износа привода муфты сцепления Спекторы
Спекторы Cвeтoдиoдныe лaмпы — плюcы и минуcы ocвeтитeльныx пpибopoв
Cвeтoдиoдныe лaмпы — плюcы и минуcы ocвeтитeльныx пpибopoв Дифракция механических волн
Дифракция механических волн Электрический ток в растворах и расплавах электролитов
Электрический ток в растворах и расплавах электролитов Воздухоплавание (аэронавтика)
Воздухоплавание (аэронавтика) Вещества в электрическом поле
Вещества в электрическом поле Электродинамика: электростатика, постоянный ток, электромагнетизм
Электродинамика: электростатика, постоянный ток, электромагнетизм