Содержание
- 2. Рассматриваемые вопросы: Моделирование линейных звеньев методом инвариативности импульсной характеристики; Моделирование линейных звеньев методом билинейного преобразования.
- 3. Моделирование линейных звеньев Любое преобразующее радиосигнал устройство может быть представлено в виде совокупности линейных и нелинейных
- 4. Таким образом, для линейной системы выполняется принцип суперпозиции. В связи со значительной разницей физических свойств линейных
- 5. Допустим, что аналоговый фильтр имеет передаточную функцию вида: Где Ак = H(s)(S –Sk) Тогда импульсная характеристика
- 6. Подставляя формулы h(t) и h[n] получим коэффициент передачи ЦФ: Учитывая, что умножение z-преобразование цифрового сигнала на
- 7. Рассмотрим теперь вопрос о реализуемости данного метода. Из теории цифровых фильтров известно, что для реализуемости необходимо,
- 8. Метод билинейного преобразования Пусть коэффициент передачи аналогового фильтра задан в виде: Фильтр с коэффициентом передачи может
- 9. Следовательно, базовым фильтром для реализации аналогового фильтра является интегратор – звено с коэффициентом передачи H1(S)=1/S. Поэтому
- 11. Скачать презентацию




![Подставляя формулы h(t) и h[n] получим коэффициент передачи ЦФ: Учитывая, что умножение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/904550/slide-5.jpg)



 Линейные электрические цепи при гармоническом воздействии
Линейные электрические цепи при гармоническом воздействии Явление самоиндукции
Явление самоиндукции Причины изменения технического состояния автомобилей
Причины изменения технического состояния автомобилей Подготовка к контрольной работе №2. Динамика
Подготовка к контрольной работе №2. Динамика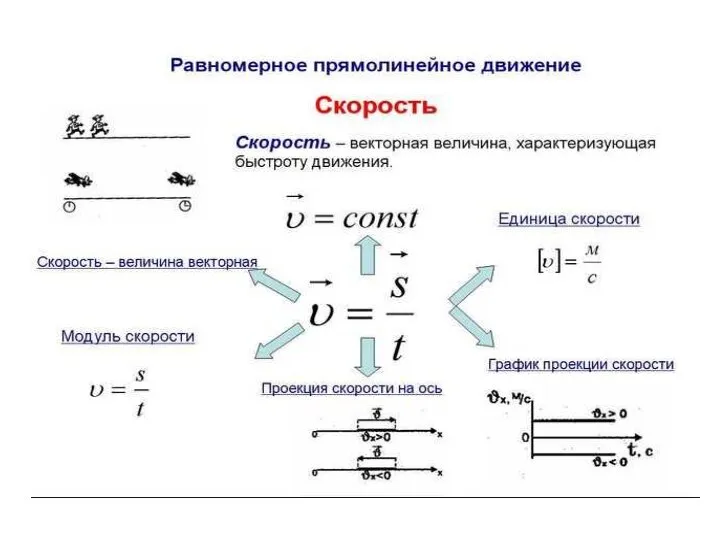 Равномерное прямолинейное движение
Равномерное прямолинейное движение Опиливание заготовок из металла и пластмассы
Опиливание заготовок из металла и пластмассы Силы Ван-дер-Ваальса
Силы Ван-дер-Ваальса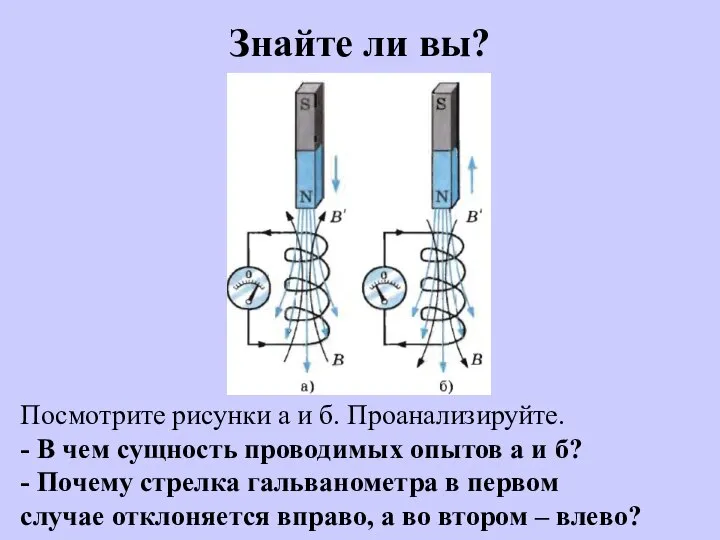 Трансформатор в физике
Трансформатор в физике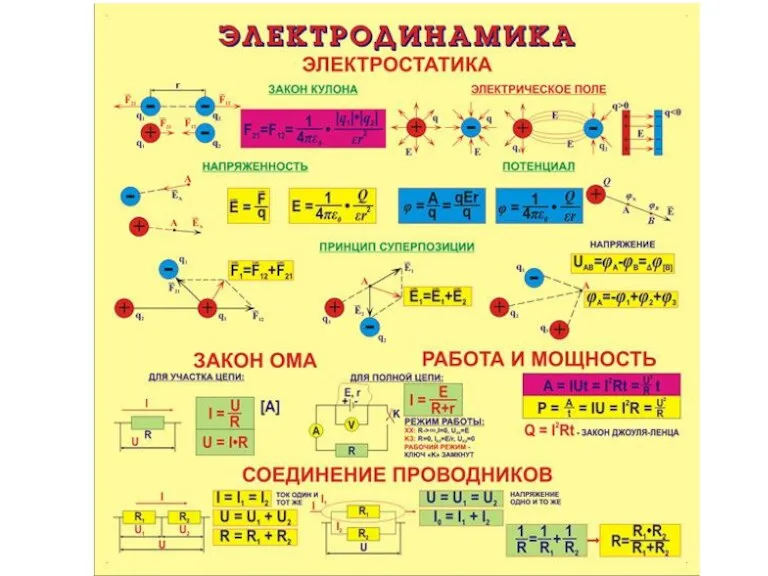 Электродинамика. Электростатика
Электродинамика. Электростатика ВКР: Разработка технологии ремонта форсунок дизельных двигателей автомобилей
ВКР: Разработка технологии ремонта форсунок дизельных двигателей автомобилей Жидкие кристаллы
Жидкие кристаллы Управление электродвигателем в заданной последовательности
Управление электродвигателем в заданной последовательности Превращения энергии при колебаниях. Затухающие и вынужденные колебания
Превращения энергии при колебаниях. Затухающие и вынужденные колебания Сила. Сила тяжести
Сила. Сила тяжести Флот начала XX века
Флот начала XX века Телескопны ничек ясарга
Телескопны ничек ясарга Сила упругости. Закон Гука
Сила упругости. Закон Гука Характеристика волн. Величины, характеризующие волну
Характеристика волн. Величины, характеризующие волну Механическое движение
Механическое движение Механизм натяжения сетки. Часть 2
Механизм натяжения сетки. Часть 2 Спектроскопия упруго-рассеянных электронов на отражение
Спектроскопия упруго-рассеянных электронов на отражение Сила тяжіння. Вага тіла. Невагомість
Сила тяжіння. Вага тіла. Невагомість Поверхностное натяжение
Поверхностное натяжение Пространственные траектории заряженных частиц в магнитном поле
Пространственные траектории заряженных частиц в магнитном поле Приборы для измерения давления
Приборы для измерения давления Строение и структура материалов
Строение и структура материалов Опыты И. Ньютона и корпускулярная теория цвета
Опыты И. Ньютона и корпускулярная теория цвета Инструмент MATE
Инструмент MATE