Содержание
- 2. Графы I. два варианта значения слова “граф”: 1) удобная форма описания структур типа дорожной сети или
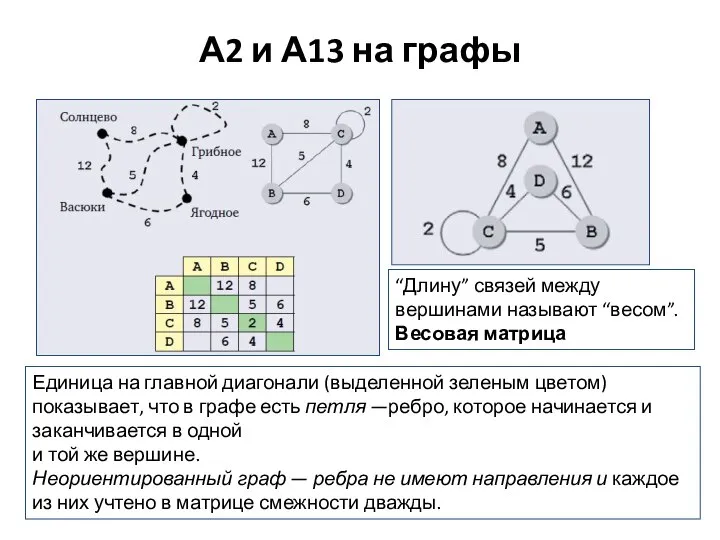
- 3. А2 и А13 на графы Единица на главной диагонали (выделенной зеленым цветом) показывает, что в графе
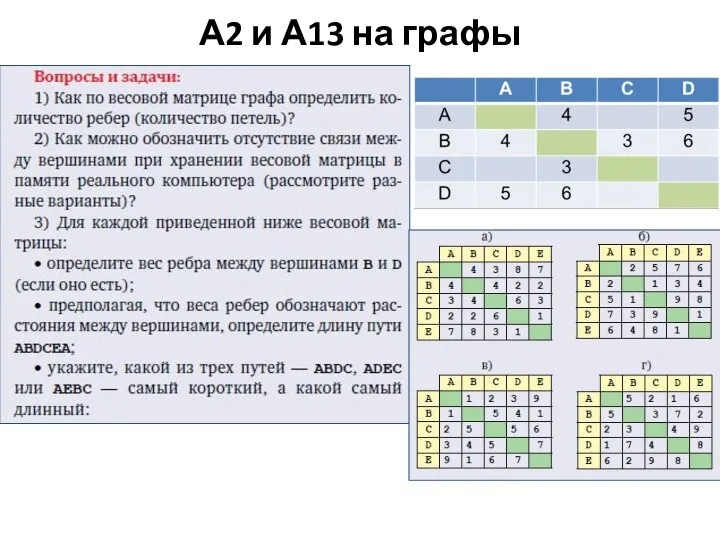
- 4. А2 и А13 на графы
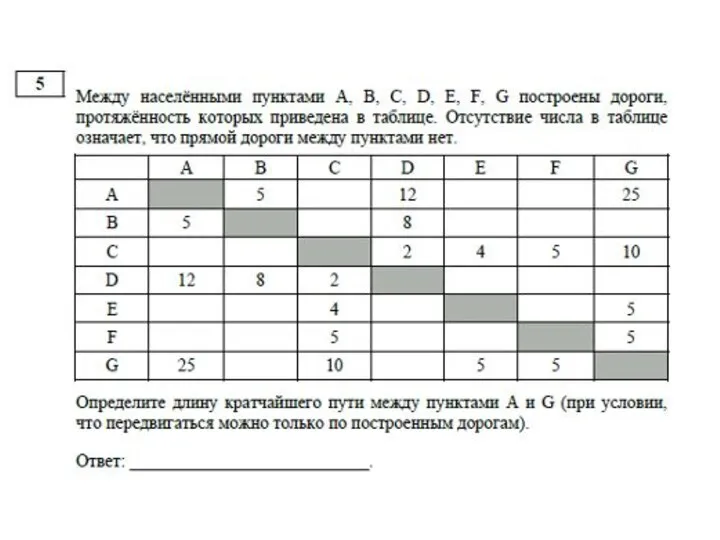
- 5. Задача на «кратчайшее расстояние» ДЕМО 2013
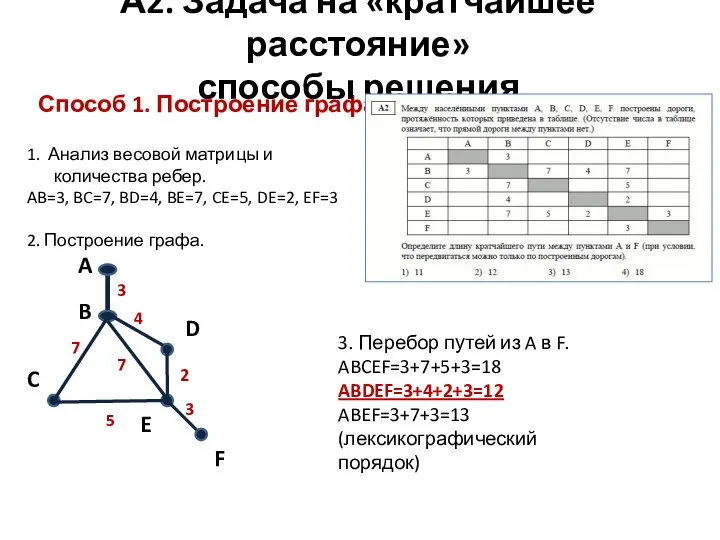
- 6. Способ 1. Построение графа. А2. Задача на «кратчайшее расстояние» способы решения 1. Анализ весовой матрицы и
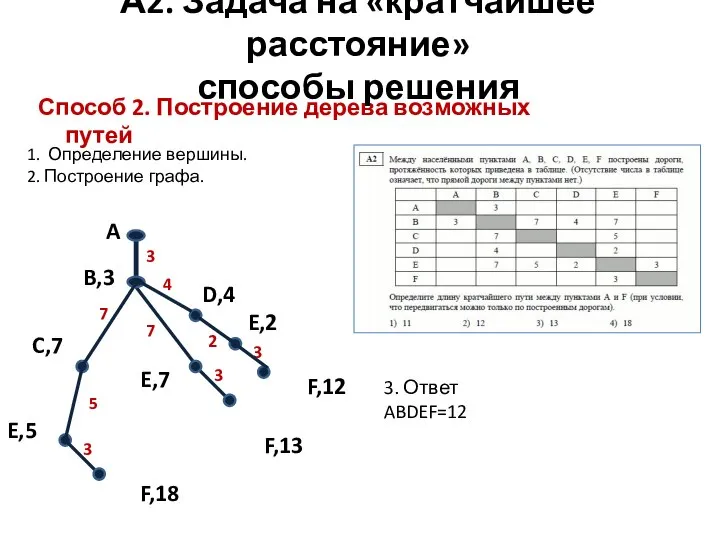
- 7. Способ 2. Построение дерева возможных путей А2. Задача на «кратчайшее расстояние» способы решения 1. Определение вершины.
- 8. А2. Задача на «кратчайшее расстояние» способы решения Способ 3. Перебор возможных путей без построения дерева 1.
- 9. А2. Задача на «кратчайшее расстояние» способы решения Способ 4. Использование алгоритма Дейкстры. Описание в статье К.Полякова
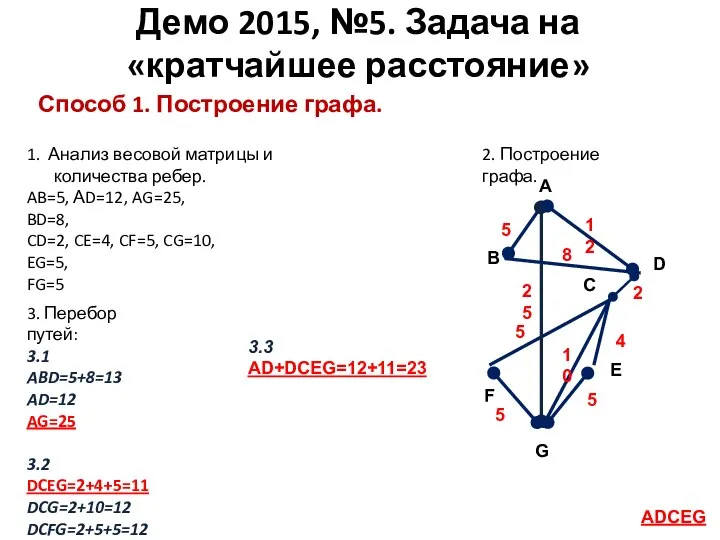
- 11. Способ 1. Построение графа. Демо 2015, №5. Задача на «кратчайшее расстояние» Анализ весовой матрицы и количества
- 12. Способ 1. Построение графа. Демо 2015, №5. Задача на «кратчайшее расстояние» 1. Анализ весовой матрицы и
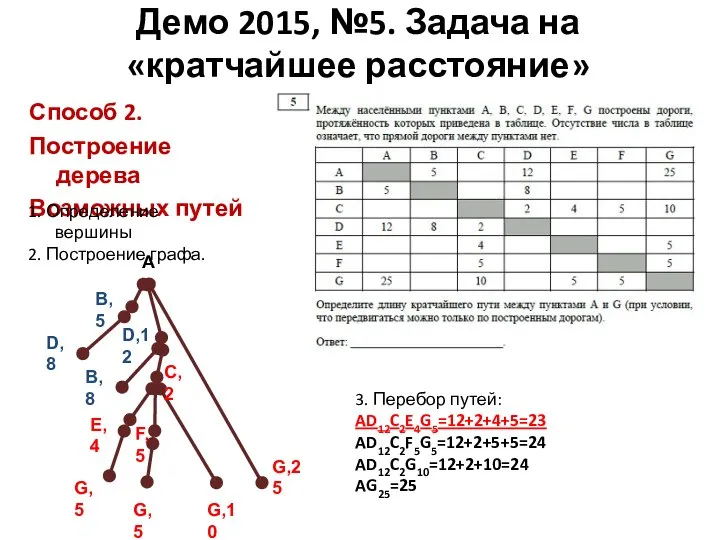
- 13. Способ 2. Построение дерева Возможных путей Демо 2015, №5. Задача на «кратчайшее расстояние» 1. Определение вершины
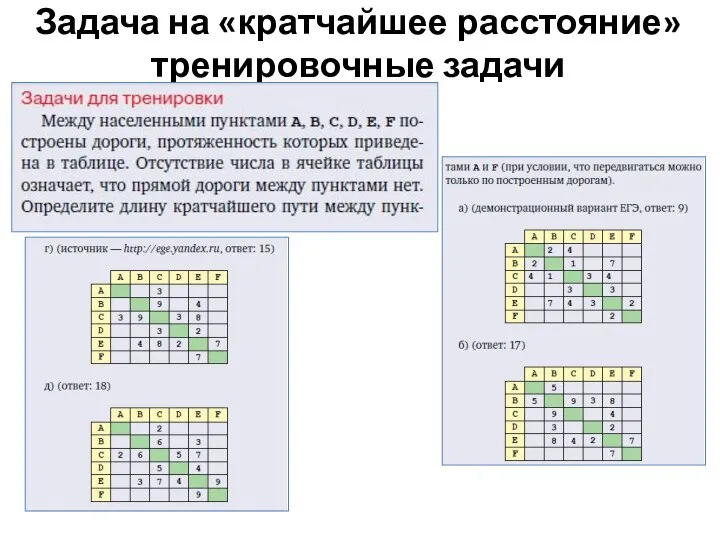
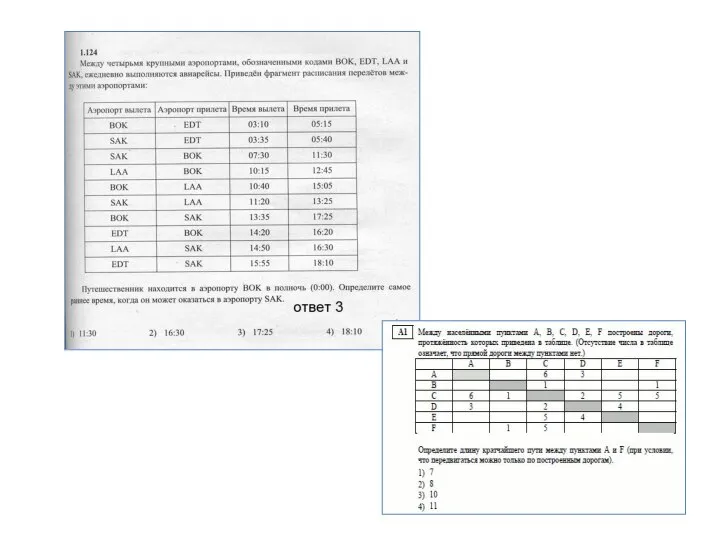
- 14. Задача на «кратчайшее расстояние» тренировочные задачи
- 15. Задача на «кратчайшее расстояние»
- 16. Задача на «кратчайшее расстояние» тренировочные задачи
- 21. Скачать презентацию









 Получение нанокапель методом сверхзвукового разшерения
Получение нанокапель методом сверхзвукового разшерения 0 гениальных изобретений Николы Тесла
0 гениальных изобретений Николы Тесла Оптика
Оптика Методы повышения конструкционной прочности деталей машин
Методы повышения конструкционной прочности деталей машин Конденсатор. Индуктивность
Конденсатор. Индуктивность Перенос графена на произвольную подложку
Перенос графена на произвольную подложку Характеристика волн
Характеристика волн Движение по окружности
Движение по окружности Сила тяжести на других планетах. Урок 27
Сила тяжести на других планетах. Урок 27 Открытие фотоэффекта
Открытие фотоэффекта Условие передачи максимума средней мощности от источника к приемнику
Условие передачи максимума средней мощности от источника к приемнику Законы геометрической оптики
Законы геометрической оптики Случайные фракталы
Случайные фракталы Применение первого закона термодинамики к изопроцессам. 10 класс
Применение первого закона термодинамики к изопроцессам. 10 класс Первый пароход 4/2 класс
Первый пароход 4/2 класс Физико-химический марафон
Физико-химический марафон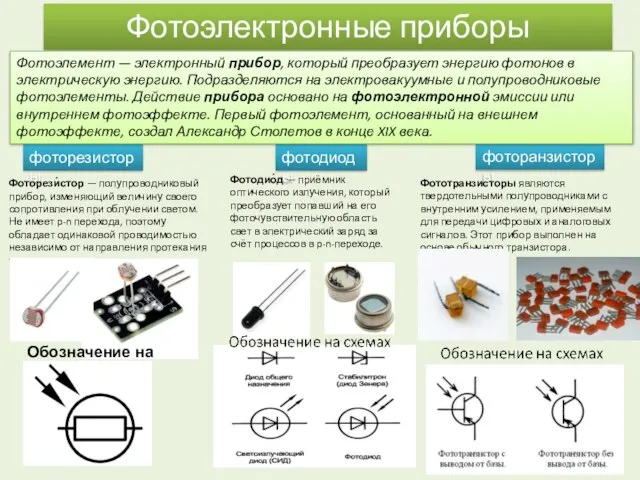 Фотоэлектронные приборы
Фотоэлектронные приборы Электромагнитная индукция
Электромагнитная индукция Познавательная игра для учащихся 9 класса Макова Л.И. МОУ Есиповская сош
Познавательная игра для учащихся 9 класса Макова Л.И. МОУ Есиповская сош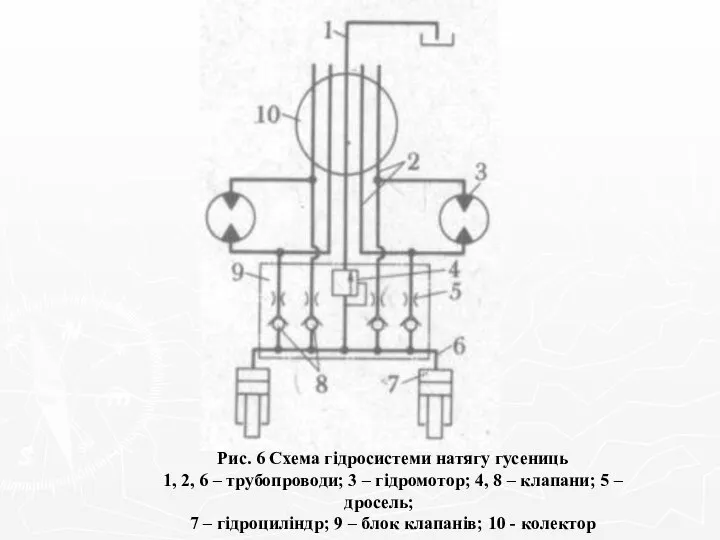 Схема гідросистеми натягу гусениць
Схема гідросистеми натягу гусениць методичка1 - Расчет тайминга движущихся предметов
методичка1 - Расчет тайминга движущихся предметов Метод переходного состояния. Классическая теория
Метод переходного состояния. Классическая теория Судостроение. Что общего у предметов?
Судостроение. Что общего у предметов? Количество вщства. Решение задач
Количество вщства. Решение задач Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Решение задач
Решение задач Механическое движение
Механическое движение Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики
Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики