Содержание
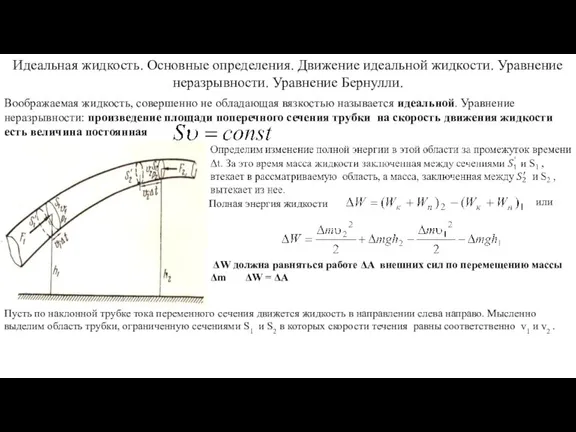
- 2. Идеальная жидкость. Основные определения. Движение идеальной жидкости. Уравнение неразрывности. Уравнение Бернулли. Воображаемая жидкость, совершенно не обладающая
- 3. Определим ΔA. Внешняя сила давления F1 совершает работу ΔA1 по перемещению втекающей массы на пути v1Δt
- 4. К жидкостям относят вещества, которые по своим свойствам занимают промежуточное положение между газами и твердыми телами.
- 5. Сила внутреннего трения пропорциональна площади S взаимодействующих слоев и тем больше, чем больше их относительная скорость.
- 6. Течение вязкой жидкости по трубам. Формула Пуазейля Течение вязкой жидкости по трубам представляет для медицины особый
- 7. Проинтегрируем это уравнение
- 8. Проведем аналогию между формулой Пуазейля и законом Ома для участка цепи без источника тока. Разность потенциалов
- 9. Общее гидравлическое сопротивление трех труб, соединенных последовательно и параллельно, вычисляется по формулам
- 10. Вязкость проявляется при движении не только жидкости по трубам, но и тел в жидкости. Наиболее простой
- 11. Формула справедлива для движения шарика не только в жидкости, но и в газе. Методы определения вязкости
- 12. Система кровообращения служит для постоянного снабжения клеток питательными веществами и газами, для обмена продуктами жизнедеятельности клеток,
- 13. Модель кровеносной системы, предложенная О. Франком. Несмотря на достаточную простоту модель позволяет установить связь между ударным
- 14. На основании уравнения Пуазейля можно записать для периферической части системы Подставляя, получаем Проинтегрируем. Пределы интегрирования по
- 15. Соответствующая кривая изображена тонкой линией на рис. и получаем зависимость объемной скорости оттока крови от времени:
- 16. На основе механической модели по аналогии может быть построена электрическая модель В более точной модели сосудистого
- 17. Двухкамерная модель лучше описывает процессы, происходящие в сосудистом русле, но и она не объясняет колебания давления
- 18. Пульсовая волна При сокращении сердечной мышцы (систола) кровь выбрасывается из сердца в аорту и отходящие от
- 19. Профиль части артерии схематически показан на рис. а — после прохождения пульсовой волны, б — в
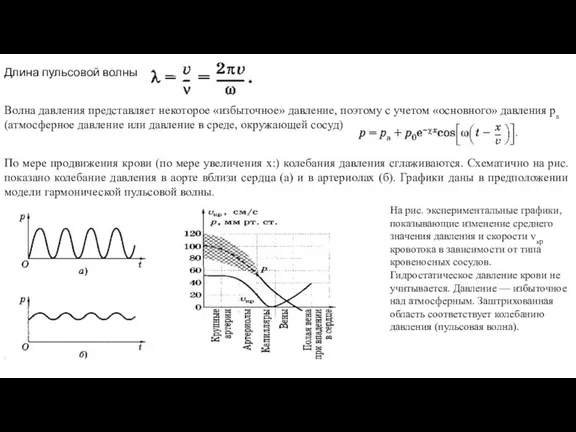
- 20. Длина пульсовой волны Волна давления представляет некоторое «избыточное» давление, поэтому с учетом «основного» давления ра (атмосферное
- 21. Скорость пульсовой волны в крупных сосудах следующим образом зависит от их параметров (формула Моенса—Кортевега): У человека
- 22. Работа и мощность сердца. Аппарат искусственного кровообращения На сообщение кинетической энергии этому объему крови затрачена работа
- 23. Пример Подставив в формулу значения р = 13 кПа, Vу = 60 мл = 6 •
- 24. Физические основы клинического метода измерения давления крови Систолическое и диастолическое давления в какой-либо артерии могут быть
- 25. Для измерения артериального давления применяют приборы, показанные на рис.: а — сфигмоманометр с ртутным манометром, б
- 26. Изучить методы : Определение скорости кровотока Ультразвуковой метод (ультразвуковая расходометрия) основан на эффекте Доплера Электромагнитный метод
- 28. Скачать презентацию























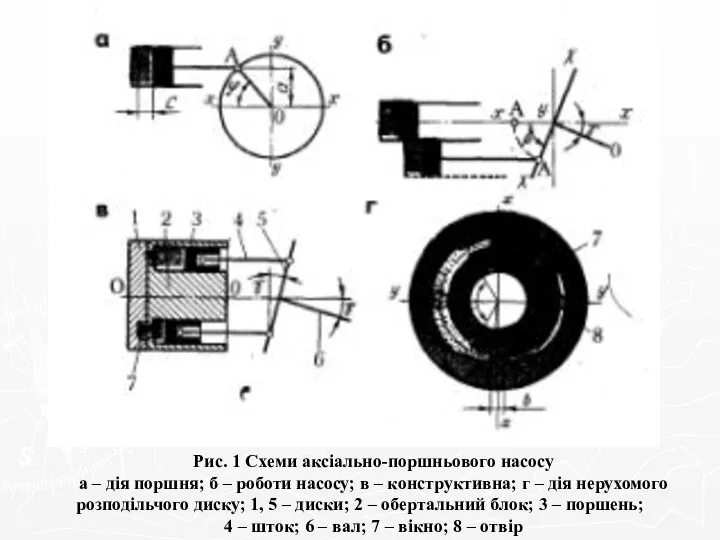 Схеми аксіально-поршньового насосу. Билет 8
Схеми аксіально-поршньового насосу. Билет 8 Презентация "Электрические явления" - скачать
Презентация "Электрические явления" - скачать Колебательный контур
Колебательный контур Импульс материальной точки. Другая формулировка второго закона Ньютона
Импульс материальной точки. Другая формулировка второго закона Ньютона Расчёт аэродинамических характеристик дозвуковых самолётов (Лекция 1)
Расчёт аэродинамических характеристик дозвуковых самолётов (Лекция 1) Определение магнитных сил
Определение магнитных сил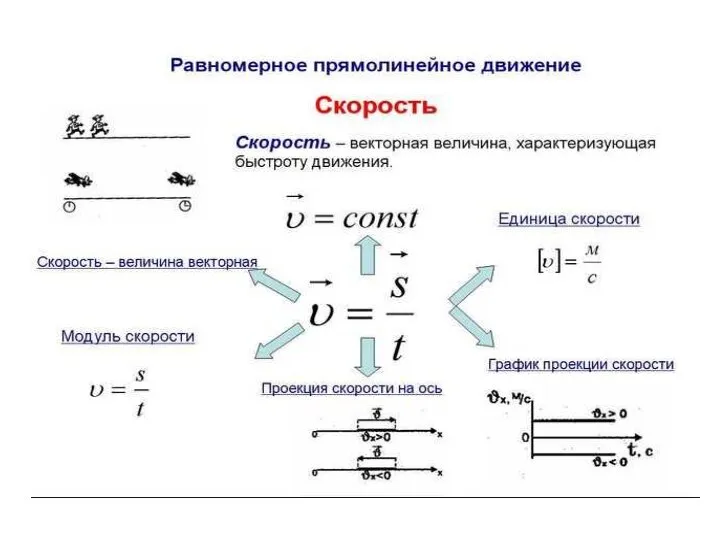 Равномерное прямолинейное движение
Равномерное прямолинейное движение 9-1 تغيير الأصوات
9-1 تغيير الأصوات Реверберация. Лекция2
Реверберация. Лекция2 Историческая справка. Звук в воздухе
Историческая справка. Звук в воздухе Начала термодинамики и термохимия
Начала термодинамики и термохимия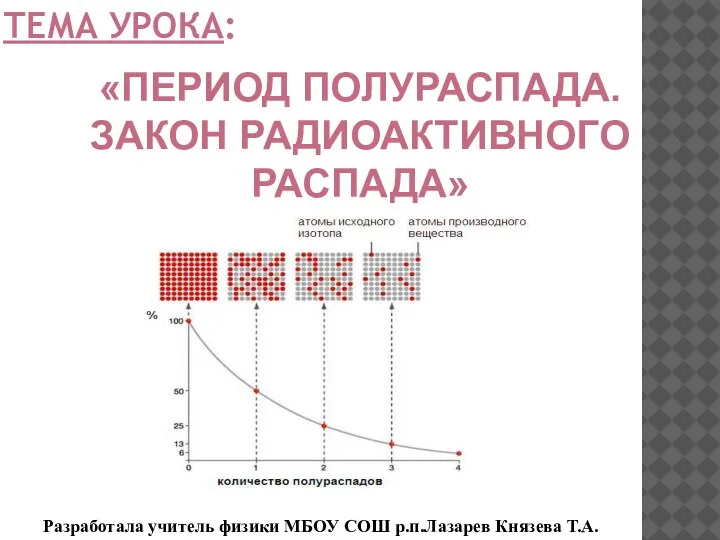 Закон радиоактивного распада. Период полураспада радиоактивных изотопов
Закон радиоактивного распада. Период полураспада радиоактивных изотопов Электрический ток в газах и в вакууме
Электрический ток в газах и в вакууме otkritie_elektromagnitnoi_indukcii
otkritie_elektromagnitnoi_indukcii Манометры поршневой жидкостный насос. Гидравлический пресс (7 класс)
Манометры поршневой жидкостный насос. Гидравлический пресс (7 класс) Ускорители заряженных частиц
Ускорители заряженных частиц 8 кл 3-4 Вн энергия. виды теплопередачи
8 кл 3-4 Вн энергия. виды теплопередачи Лед и соль!
Лед и соль! Определение скоростей точек тела при плоскопараллельном движении
Определение скоростей точек тела при плоскопараллельном движении Загадочные явления
Загадочные явления Мимеография
Мимеография Профессия механик
Профессия механик Презентация на тему Виды теплопередачи. Конвекция
Презентация на тему Виды теплопередачи. Конвекция  Experimental studies of modular generator
Experimental studies of modular generator Физическое явление. Оценка ответов учащихся
Физическое явление. Оценка ответов учащихся График плавления и отвердевания кристаллических тел
График плавления и отвердевания кристаллических тел Электротехника и электрооборудование автомобилей
Электротехника и электрооборудование автомобилей Фигуры Хладни, влияние звука на песок
Фигуры Хладни, влияние звука на песок