Определение скоростей точек тела при плоскопараллельном движении

Аналитический метод
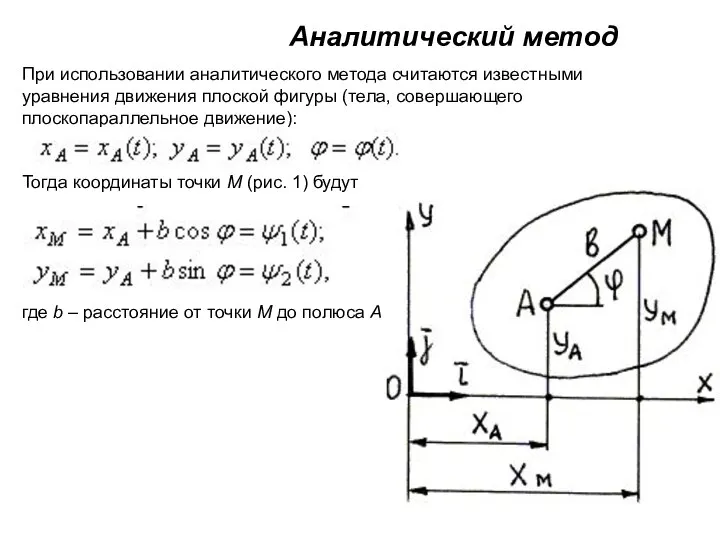
При использовании аналитического метода считаются известными уравнения движения плоской фигуры (тела, совершающего плоскопараллельное движение):
Тогда координаты точки М (рис. 1) будут
где b – расстояние от точки М до полюса А.

Модуль скорости точки М определяется по формуле
Направление вектора определяется по направляющим косинусам:
Таким образом, задача по определению скоростей точек плоской фигуры сводится к известному решению соответствующей задачи кинематики точки.
Угловая скорость плоской фигуры определяется дифференцированием последнего уравнения, т.е.
Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры

Определение скоростей точек звеньев плоских механизмов
Последовательность решения задач по определению скоростей для плоских механизмов.
1. Изобразить механизм на расчетной схеме в том положении, для которого требуется решить задачу о скоростях.
2. Определить скорости точек звена, движение которого задано по условию задачи. Это звено принято называть ведущим. Может оказаться, что ведущее звено совершает не плоскопараллельное, а вращательное движение. Тогда задача о скоростях решается методом, разработанным для вращательного движения.
3. Определить скорости точек звена, присоединенного к ведущему звену, имея в виду, что скорость точки в месте соединения этих звеньев должна быть определена ранее в п. 2.
4. Если число звеньев в механизме больше двух, то после п. 3 определяются скорости точек третьего и последующих звеньев. Скорости точек в местах соединения звеньев всегда определяются на предшествующем этапе вычислений.

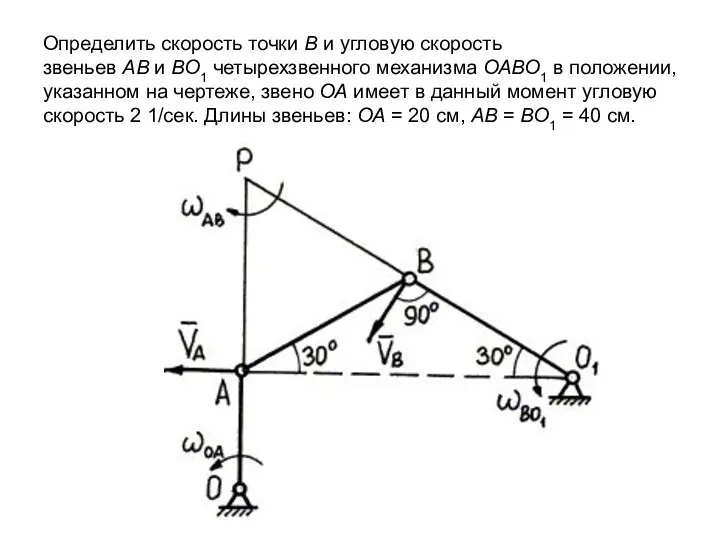
Определить скорость точки В и угловую скорость звеньев АВ и ВО1 четырехзвенного механизма ОАВО1 в положении, указанном на чертеже, звено ОА имеет в данный момент угловую скорость 2 1/сек. Длины звеньев: ОА = 20 см, АВ = ВО1 = 40 см.