Содержание
- 2. Содержание
- 3. Корпускулярно-волновая природа света Несмотря на огромные успехи электромагнитной теории света к концу XIX века начали накапливаться
- 4. Макс Планк в 1900 г. на новой основе возродил идею Декарта-Ньютона о корпускулярной природе света. Планк
- 5. Квант света
- 8. Планку удалось объяснить все закономерности в излучении абсолютно-черного тела. В 1905 году Альберт Эйнштейн объяснил закономерности
- 9. Корпускулярно-волновой дуализм Корпускулярная теория – поток частиц (корпускул); 2. Волновая теория - свет представляет собой электромагнитную
- 10. Свет - сложный объект, в одних случаях проявляются его волновые свойства в других корпускулярные (на расстояние
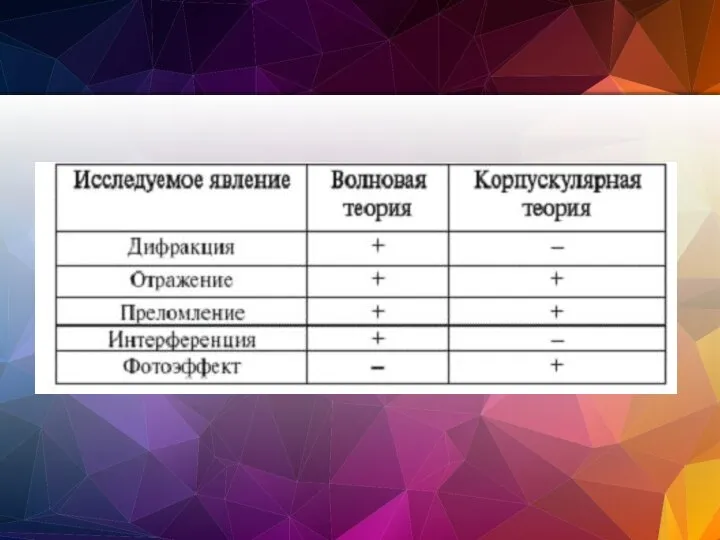
- 11. Свет обладает корпускулярно - волновым дуализмом и световые явления можно разделить на две группы: волновые и
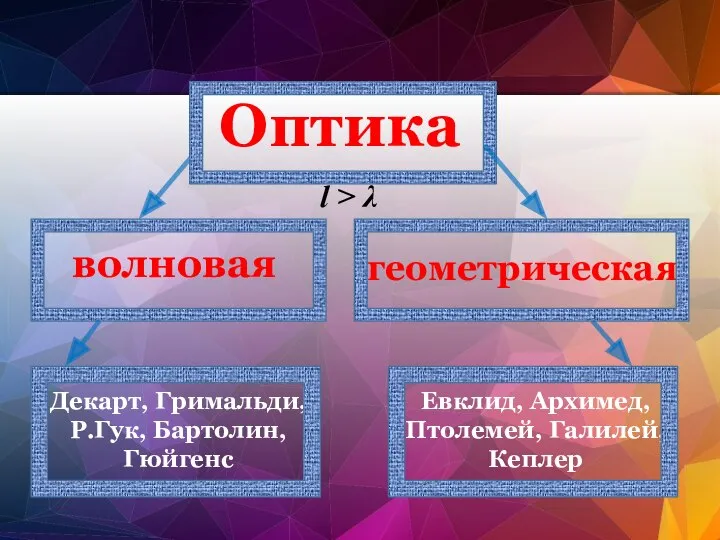
- 12. Оптика l > λ волновая геометрическая Декарт, Гримальди, Р.Гук, Бартолин, Гюйгенс Евклид, Архимед, Птолемей, Галилей, Кеплер
- 13. Геометрическая оптика Геометрическая оптика оперирует понятием светового луча. Он указывает направление распространения света, но не сами
- 14. Законы геометрической оптики 2.Закон независимости световых лучей - при пересечении световые лучи не возмущают друг друга.
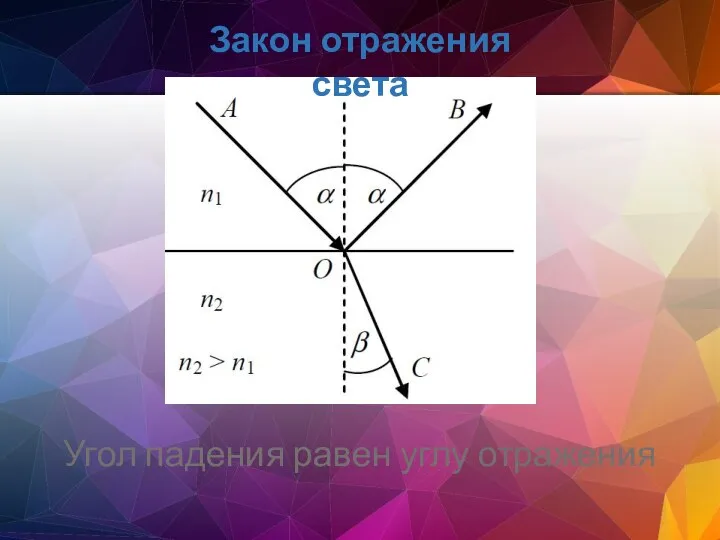
- 15. Угол падения равен углу отражения Закон отражения света
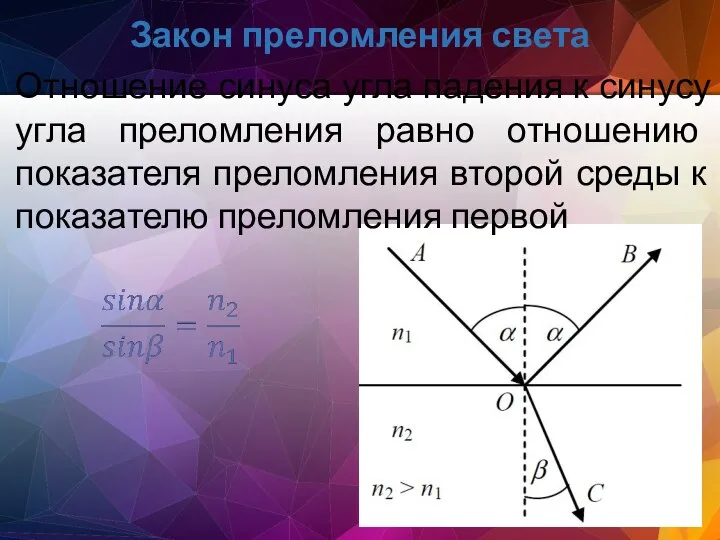
- 16. Закон преломления света Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй
- 18. Абсолютным показателем преломления равен отношению скорости света c в вакууме к скорости света υ в среде:
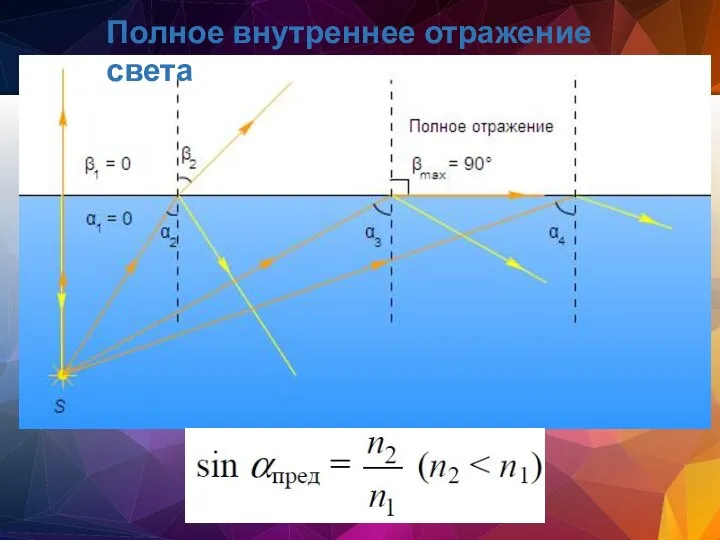
- 19. Полное внутреннее отражение света
- 20. Линзы Линзу можно представить как фигуру, образованную пересечением двух сфер. У некоторых линз одна из боковых
- 21. Линза –оптически прозрачное тело, ограниченное двумя сферическими поверхностями
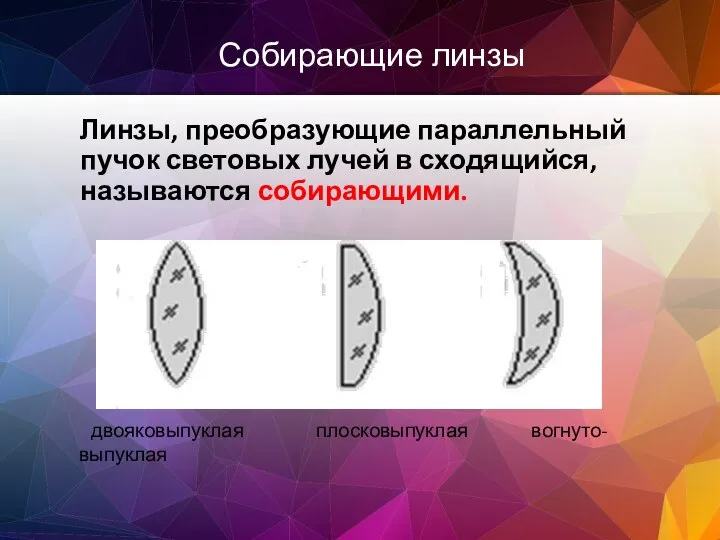
- 23. Собирающие линзы Линзы, преобразующие параллельный пучок световых лучей в сходящийся, называются собирающими.
- 24. Рассеивающие линзы Линзы, преобразующие параллельный пучок световых лучей в расходящийся, называются рассеивающими.
- 25. Тонкая линза Линза, толщина которой пренебрежимо мала по сравнению с радиусами кривизны ее поверхности называют тонкой.
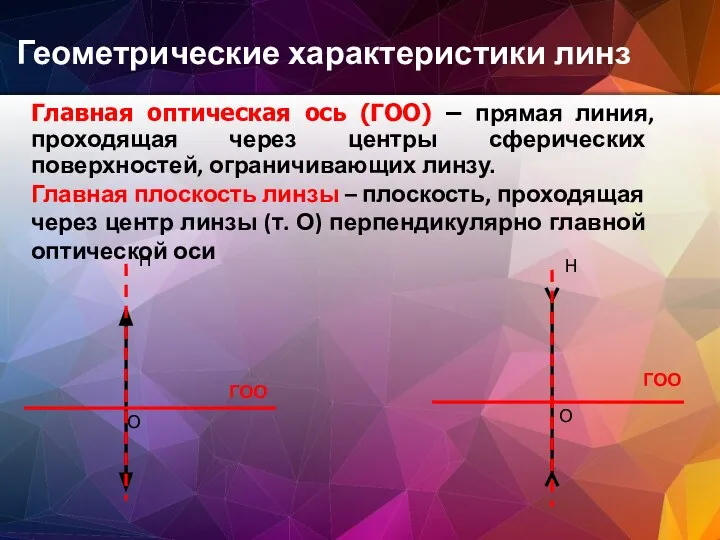
- 26. Геометрические характеристики линз Главная оптическая ось (ГОО) – прямая линия, проходящая через центры сферических поверхностей, ограничивающих
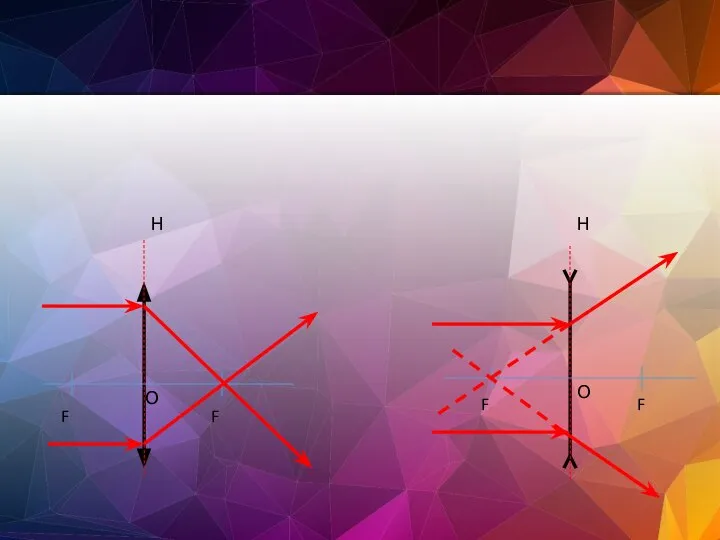
- 27. Фокус собирающей линзы – точка на главной оптической оси, в которой собираются лучи, падающие параллельно главной
- 28. Н Н О О F F F F
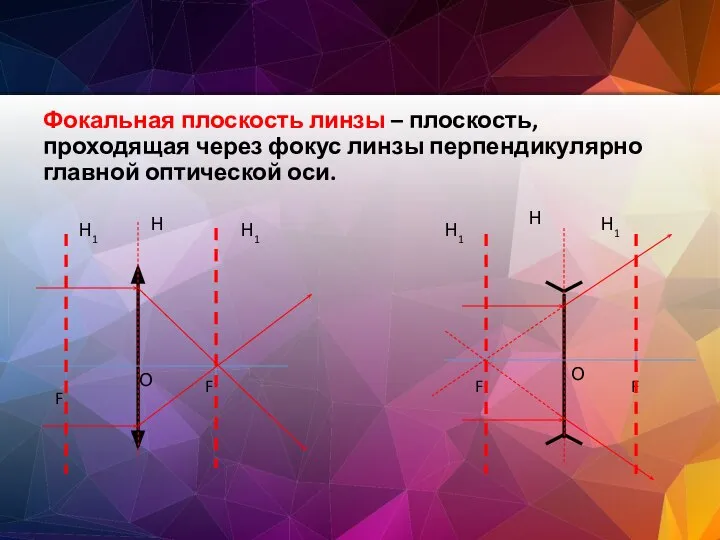
- 29. Фокальная плоскость линзы – плоскость, проходящая через фокус линзы перпендикулярно главной оптической оси. Н Н1 Н1
- 30. O - оптический центр - это точка, лежащая на оптической оси, через которую любой луч проходит
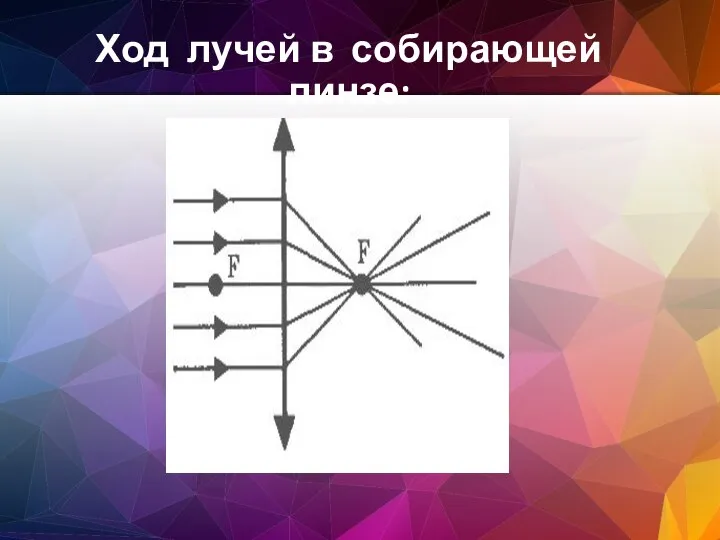
- 31. Ход лучей в собирающей линзе:
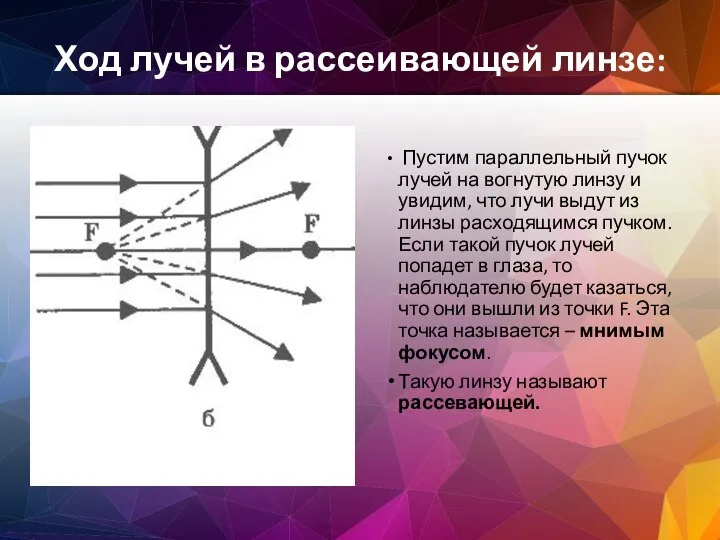
- 32. Ход лучей в рассеивающей линзе: Пустим параллельный пучок лучей на вогнутую линзу и увидим, что лучи
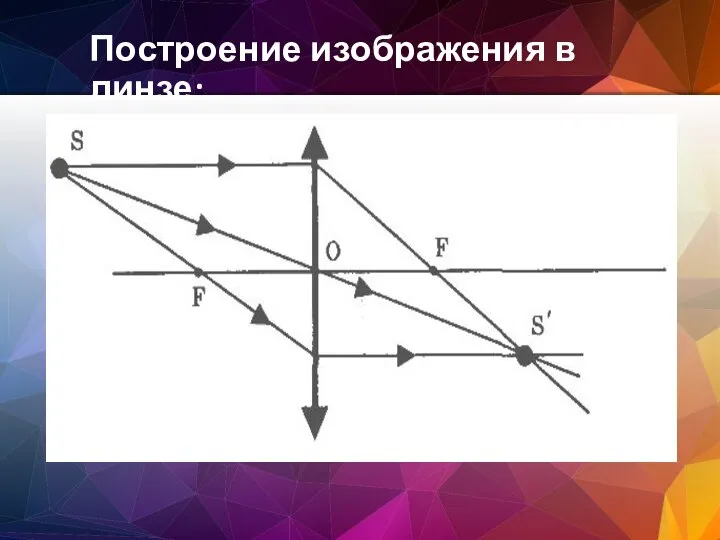
- 33. Построение изображения в линзе: Луч, падающий на линзу параллельно оптической оси, после преломления идет через фокус
- 34. 1) Лучи, проходящие через оптический центр линзы (О), не преломляются. 2) Лучи, параллельные главной оптической оси,
- 35. Формула тонкой линзы где F – фокусное расстояние; d – расстояние от предмета до линзы; f
- 36. Линза собирающая, то 1/F > 0, линза рассеивающая, то перед 1/F указывают знак « - ».
- 37. Линейным увеличением линзы называют параметр, выражающий соотношение размеров изображения Н к размерам предмета h. Для его
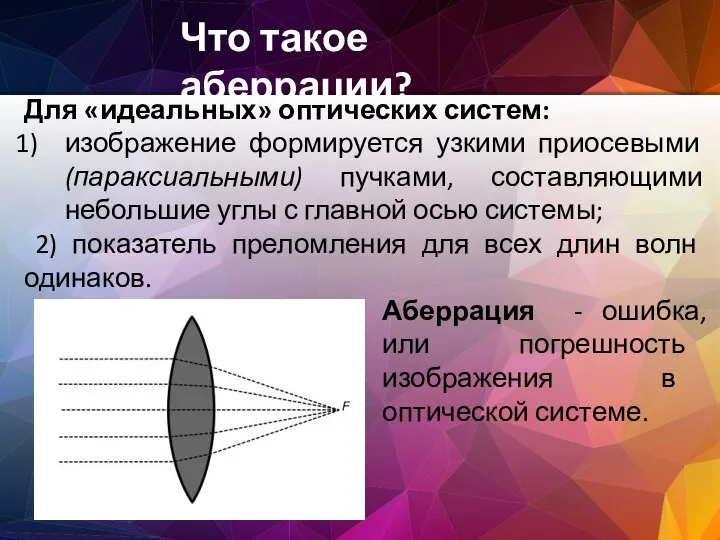
- 38. Что такое аберрации? Для «идеальных» оптических систем: изображение формируется узкими приосевыми (параксиальными) пучками, составляющими небольшие углы
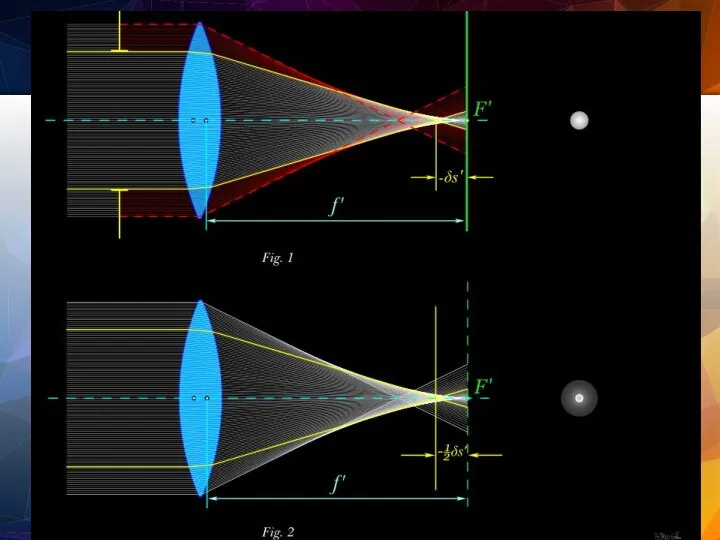
- 39. Сферическая аберрация Лучи, падающие на края линзы, собираются ближе к линзе, чем лучи, падающие на центральную
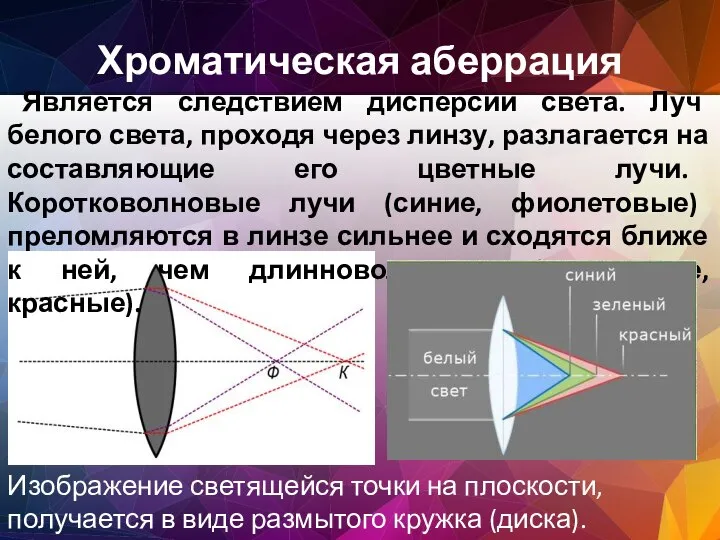
- 41. Хроматическая аберрация Является следствием дисперсии света. Луч белого света, проходя через линзу, разлагается на составляющие его
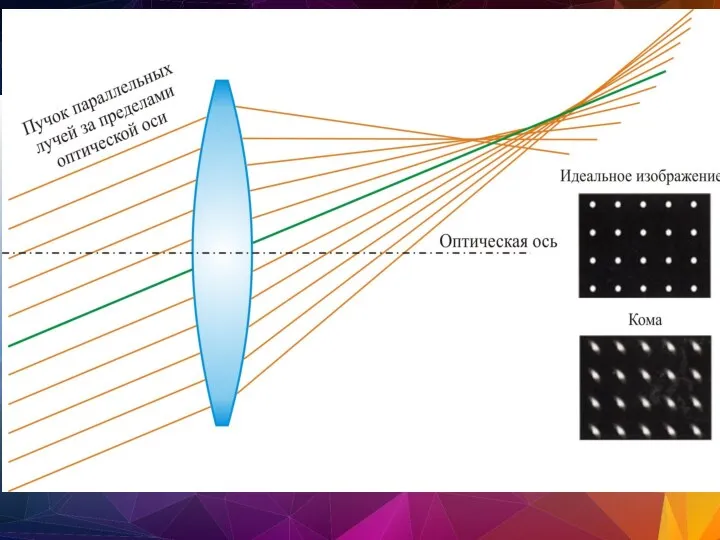
- 43. Кома Вид сферической аберрации для внеосевых (наклонных) лучей. Лучи, приходящие под углом к оптической оси не
- 46. Дисторсия изображения Лучи, участвующие в построении изображения, образуют достаточно большие углы с главной оптической осью, увеличение
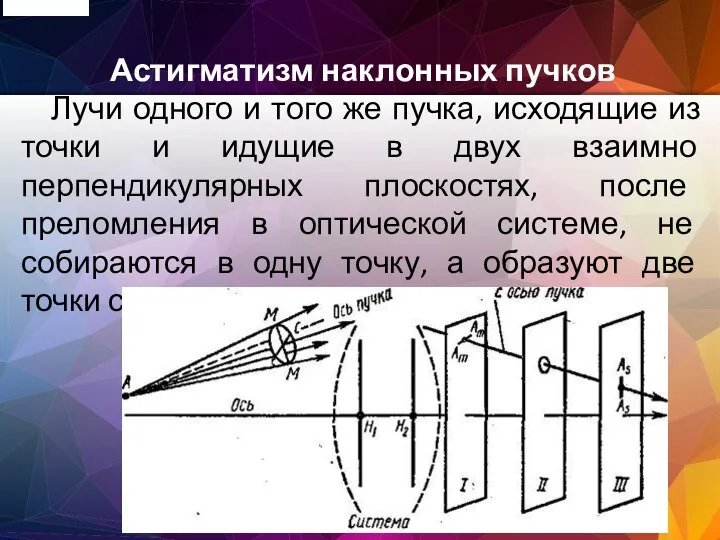
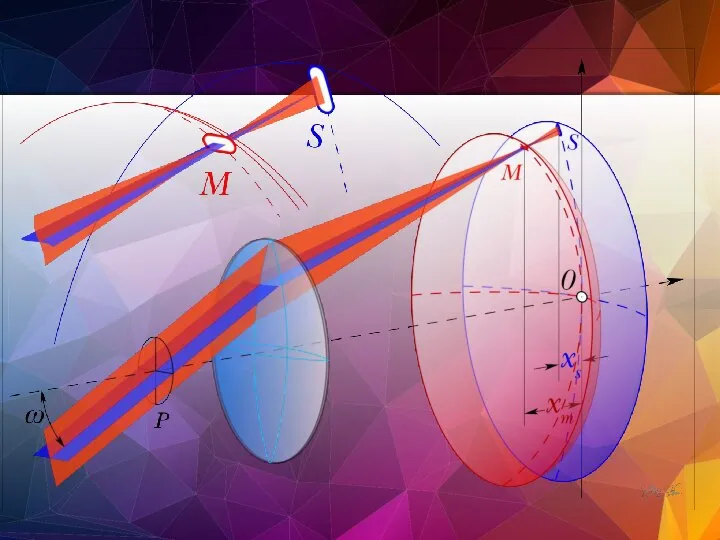
- 48. Астигматизм наклонных пучков Лучи одного и того же пучка, исходящие из точки и идущие в двух
- 51. Интерференция
- 53. Воспользуемся простейшими тригонометрическими преобразованиями:
- 55. Условие когерентности Если разность фаз гармонических колебаний одинаковой частоты остается постоянной во времени, то возникающие волны
- 57. Результат наложения волн Если встречаются друг с другом два фронта волн с одинаковой фазой, то возникает
- 58. Открытие интерференции Интерференция света наблюдались ещё Ньютоном в 17 в., однако он не смог объяснить её
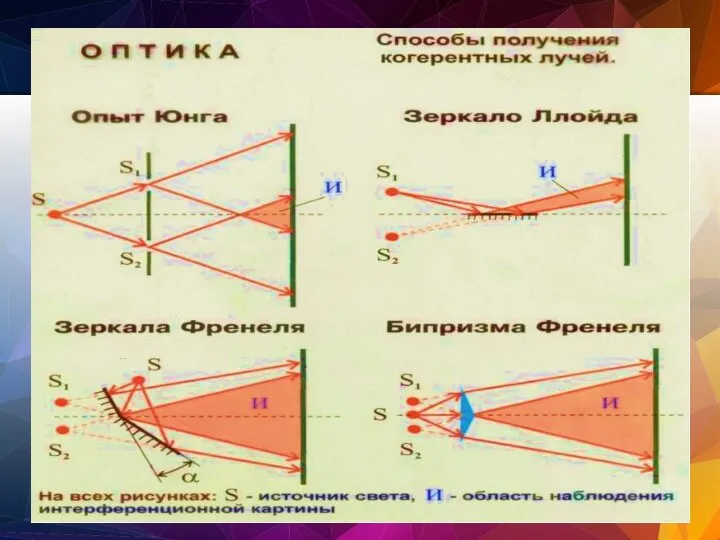
- 59. 1) разделение волны по фронту (опыт Юнга, бипризма Френеля, бизеркала Френеля, зеркала Ллойда, билинза Бийе); 2)
- 60. Способы получения когерентных волн Бипризма Френеля Зеркало Ллойда
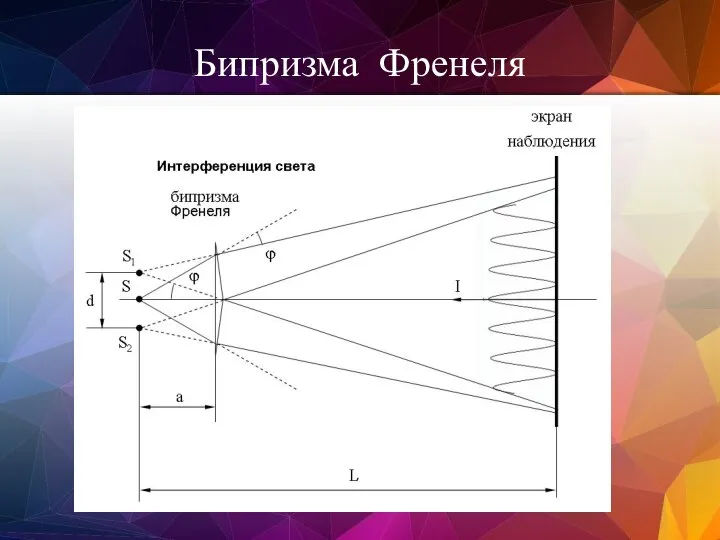
- 61. Бипризма Френеля- двойная призма с очень малыми углами при вершинах, как бы составленная из двух сложенных
- 62. Бипризма Френеля
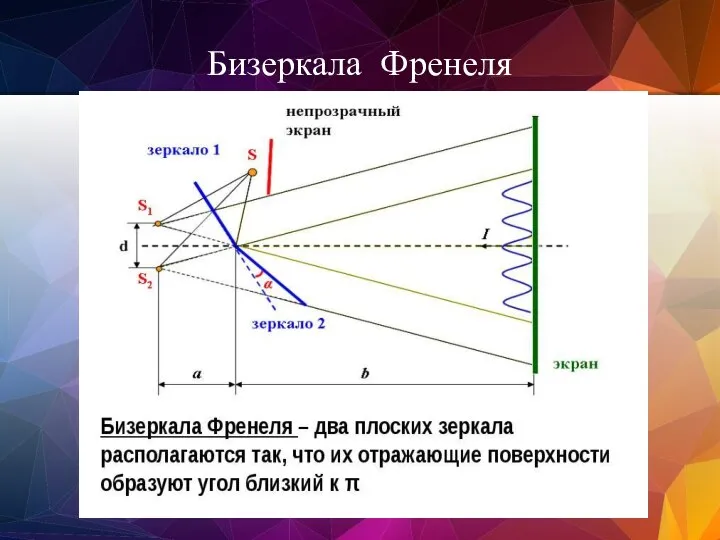
- 63. Бизеркала Френеля
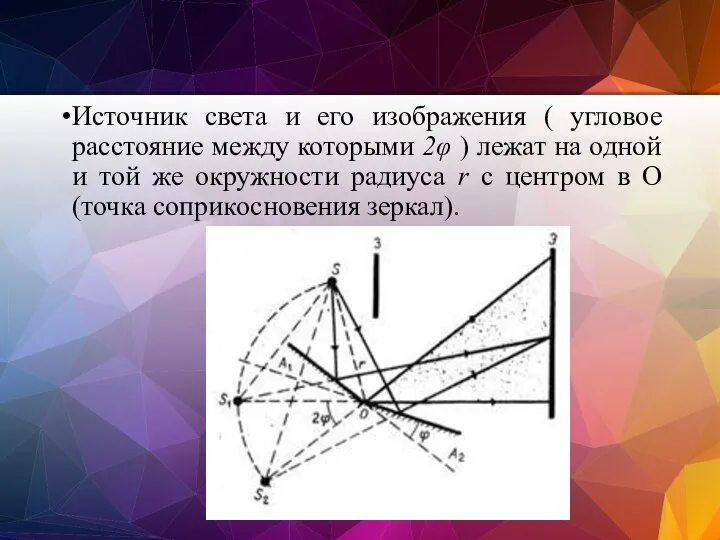
- 64. Источник света и его изображения ( угловое расстояние между которыми 2φ ) лежат на одной и
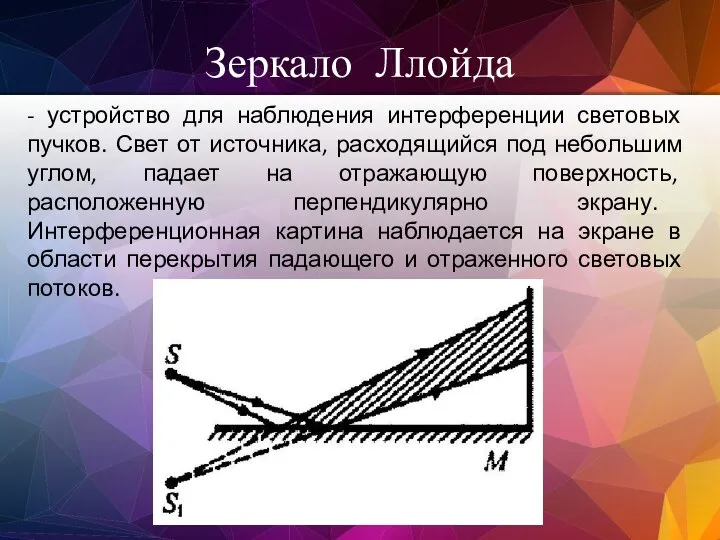
- 65. Зеркало Ллойда - устройство для наблюдения интерференции световых пучков. Свет от источника, расходящийся под небольшим углом,
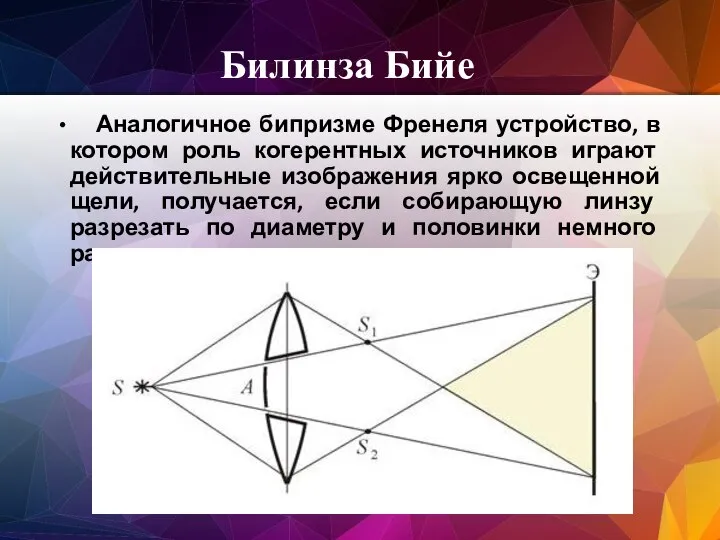
- 66. Билинза Бийе Аналогичное бипризме Френеля устройство, в котором роль когерентных источников играют действительные изображения ярко освещенной
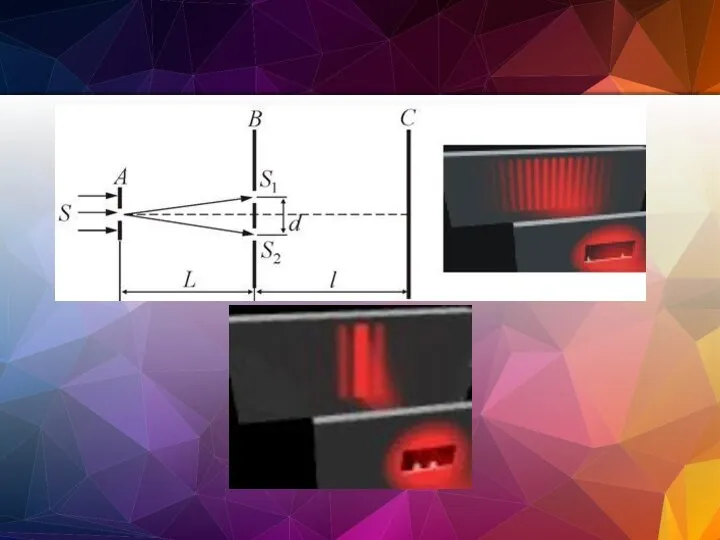
- 67. Опыт Юнга 1802 г
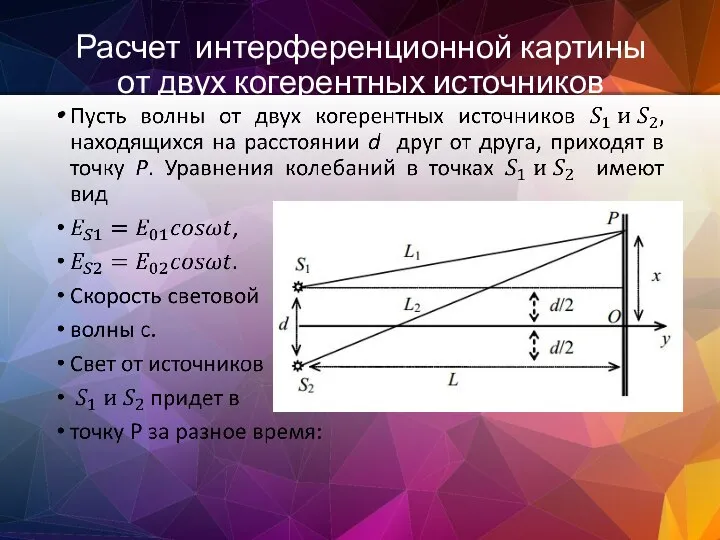
- 69. Расчет интерференционной картины от двух когерентных источников
- 71. Интерференционные экстремумы
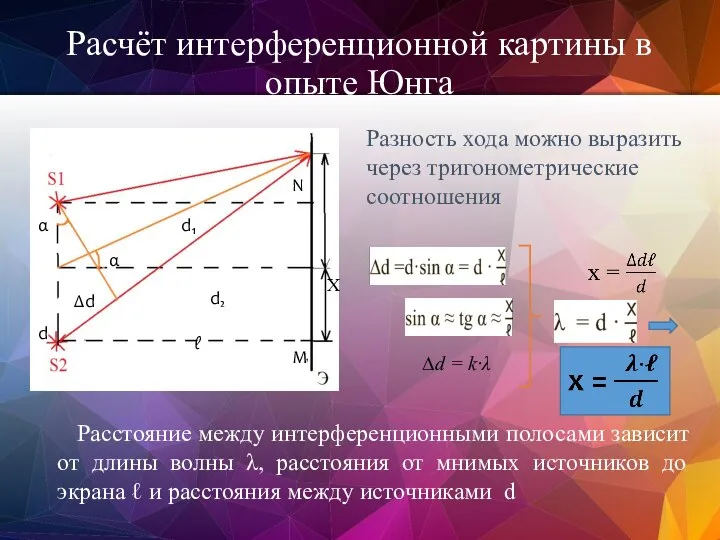
- 74. Расчёт интерференционной картины в опыте Юнга α α Х ∆d M N d d₁ d₂ ℓ
- 75. Интерференция в тонких плёнках Причина: отражение от внешней поверхности плёнки, а другая – от внутренней. Тонкая
- 76. Интерференция в тонких плёнках Рассмотрим плоскопараллельную тонкую пластину, показатель преломления которой равен n, а толщина равна
- 77. На поверхности такой пленки, в некоторой точке А луч делится. Он частично отражается от верхней поверхности
- 79. Интерференция в тонких плёнках
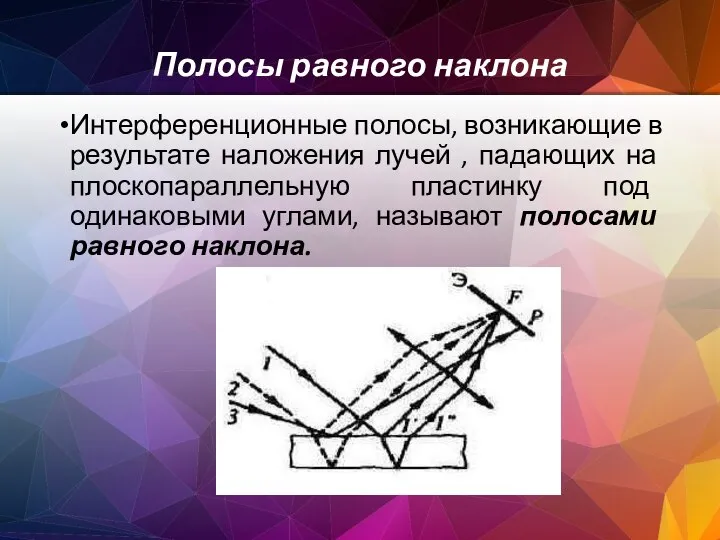
- 80. Полосы равного наклона (интерференция от плоскопараллельной пластинки)
- 81. Полосы равного наклона Интерференционные полосы, возникающие в результате наложения лучей , падающих на плоскопараллельную пластинку под
- 82. Полосы равного наклона Лучи 1’ и 1” , отразившиеся от верхней и нижней граней пластинки, параллельны
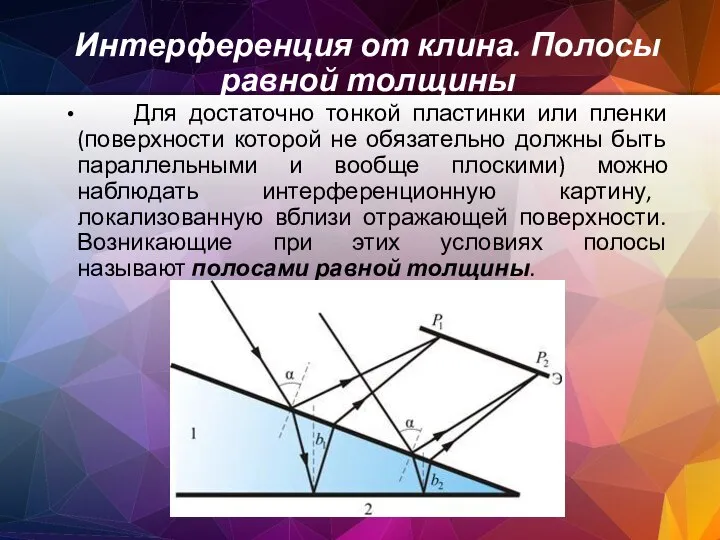
- 83. Интерференция от клина. Полосы равной толщины Для достаточно тонкой пластинки или пленки (поверхности которой не обязательно
- 84. В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цветами тонких пленок. Его легко наблюдать
- 85. Результат интерференции в точках P1 и P2 экрана определяется по формуле , подставляя в неё толщину
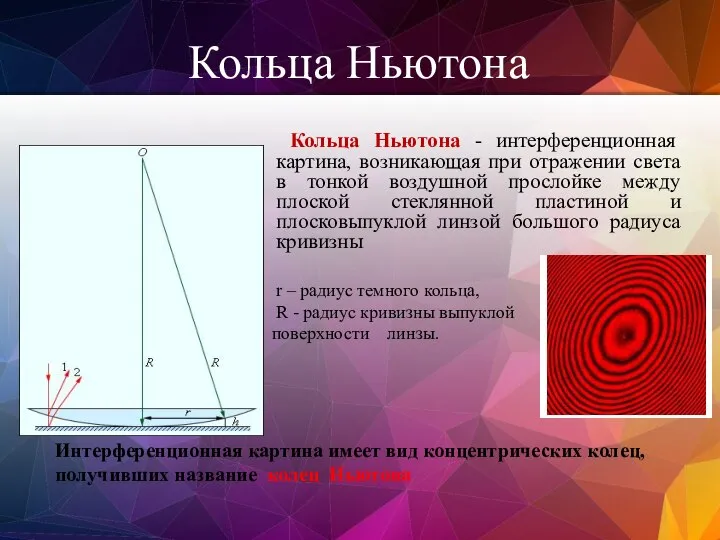
- 86. Кольца «Ньютона» Интерференционные полосы равной толщины в форме колец, расположенных концентрически вокруг точки касания двух сферических
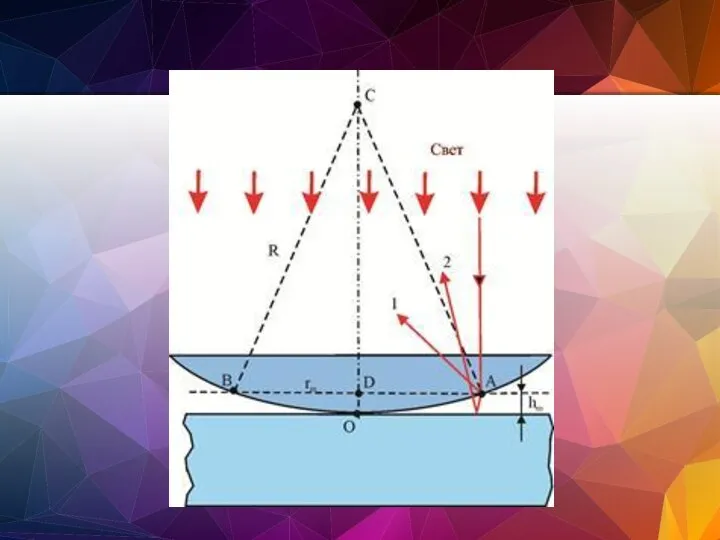
- 87. Кольца Ньютона - интерференционная картина, возникающая при отражении света в тонкой воздушной прослойке между плоской стеклянной
- 89. В отраженном свете интерференционная картина является результатом сложения когерентных волн 1 и 2, отраженных от сферической
- 90. При нормальном падении света кольца в отраженном свете имеют вид концентрических окружностей с центром в точке
- 91. Сначала запишем условие образования темных колец. Они возникают там, где оптическая разность хода волн, отраженных от
- 94. ДИФРАКЦИЯ СВЕТА Дифракция света – явление огибания световыми волнами границ непрозрачных тел, с образованием интерференционного перераспределения
- 96. Метод зон Френеля Фронт волны разделяется на зоны таким образом, чтобы волны от двух соседних зон
- 97. Метод зон Френеля Для расчета результата действия когерентных источников всего фронта Ф Френель предложил провести ряд
- 99. Суммарная амплитуда от воздействия всего фронта Ф в точке М равна , т.е. эквивалентна половине воздействия
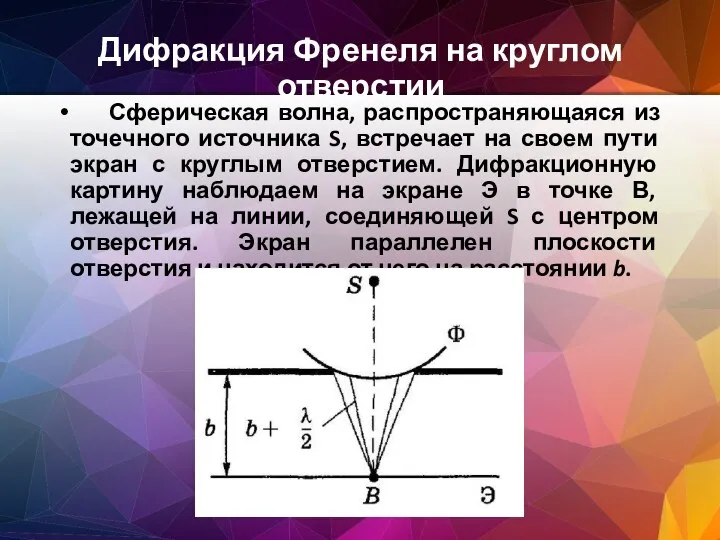
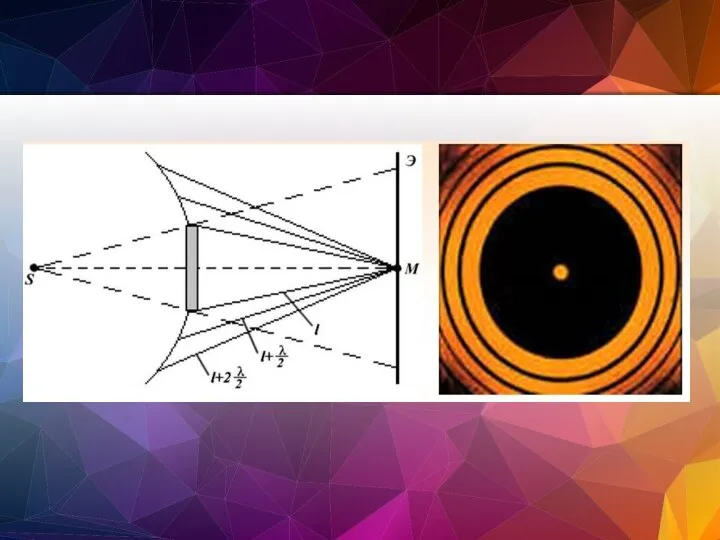
- 100. Дифракция Френеля на круглом отверстии Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути
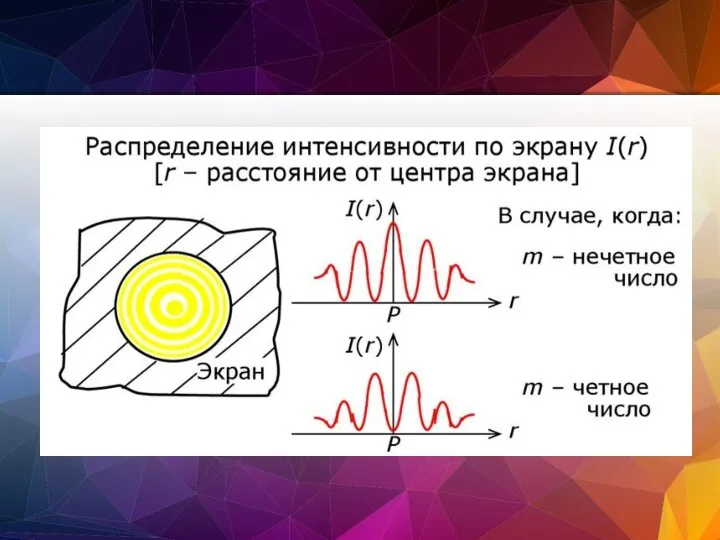
- 104. Дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец
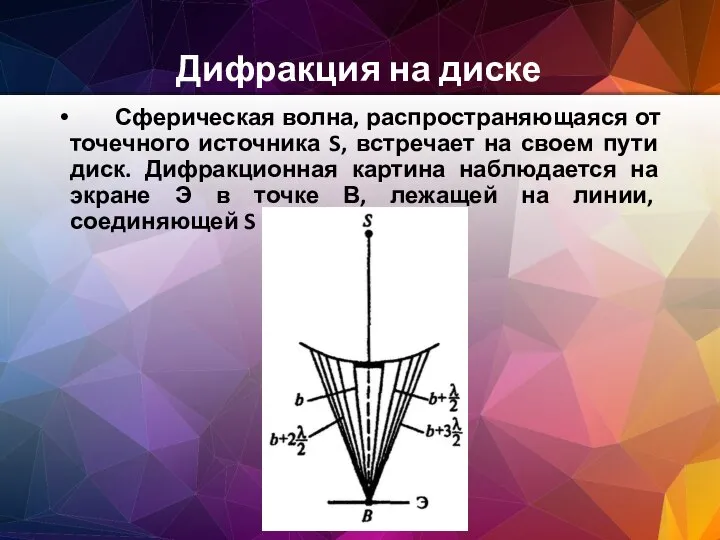
- 106. Дифракция на диске Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционная
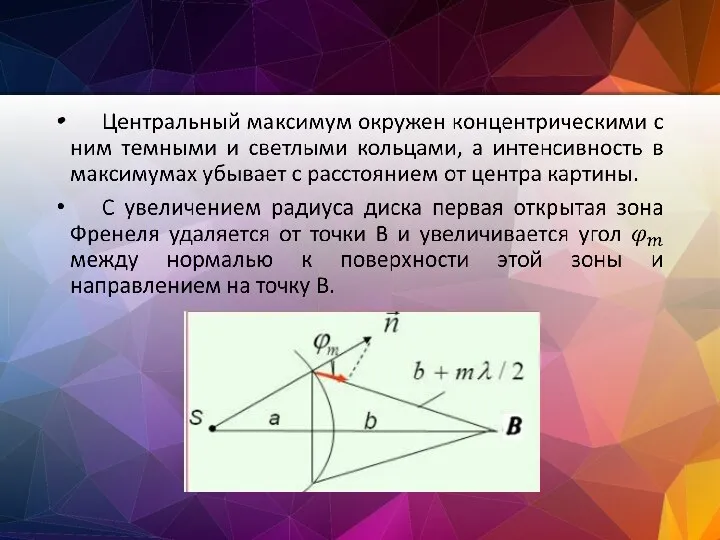
- 111. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним
- 112. Дифракция Фраунгофера
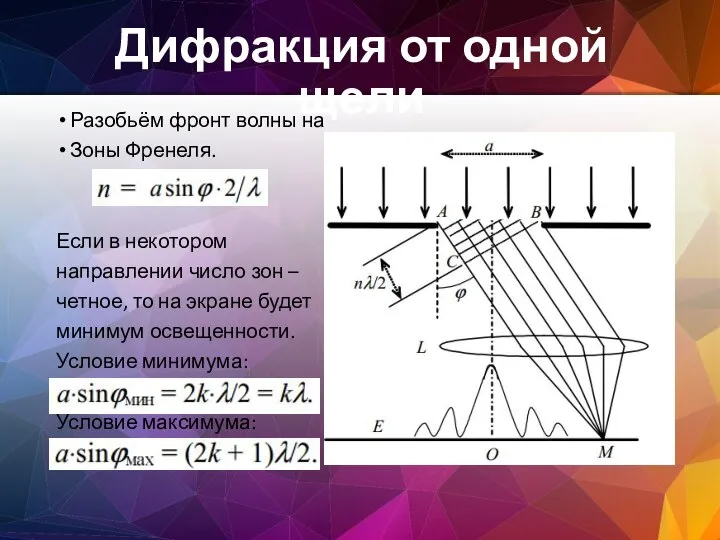
- 113. Дифракция от одной щели Разобьём фронт волны на Зоны Френеля. Если в некотором направлении число зон
- 114. Из опыта и соответствующих расчетов следует, что сужение щели приводит к тому, что центральный максимум расплывается,
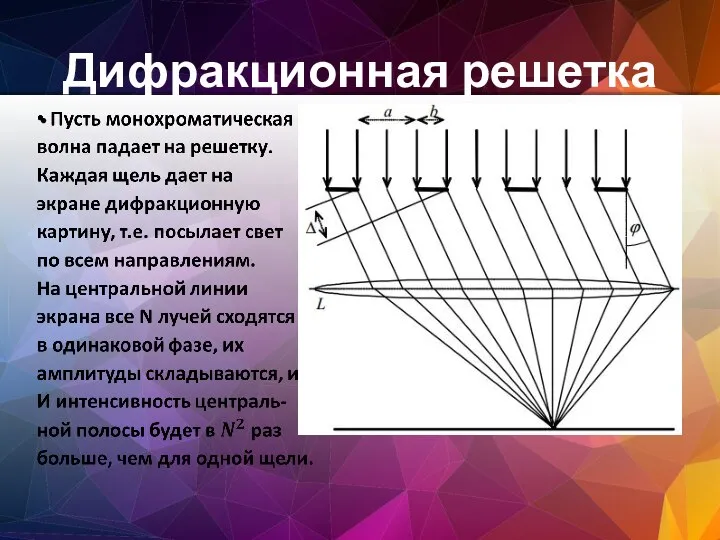
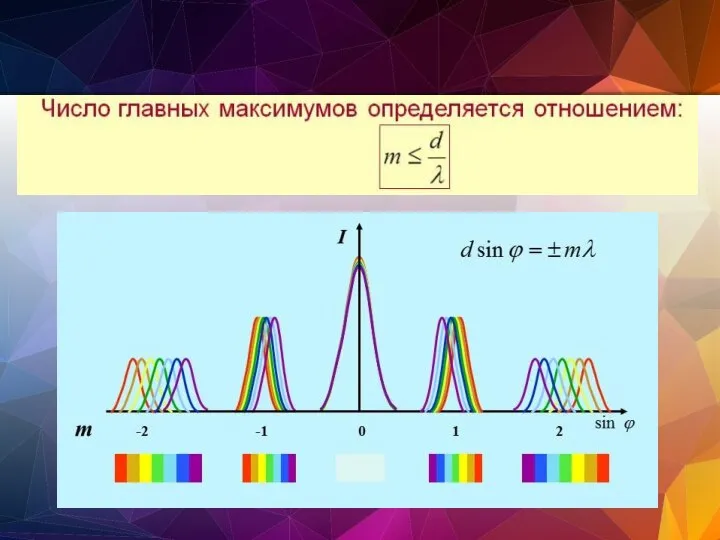
- 115. Дифракционная решетка
- 118. Дифракционная решетка
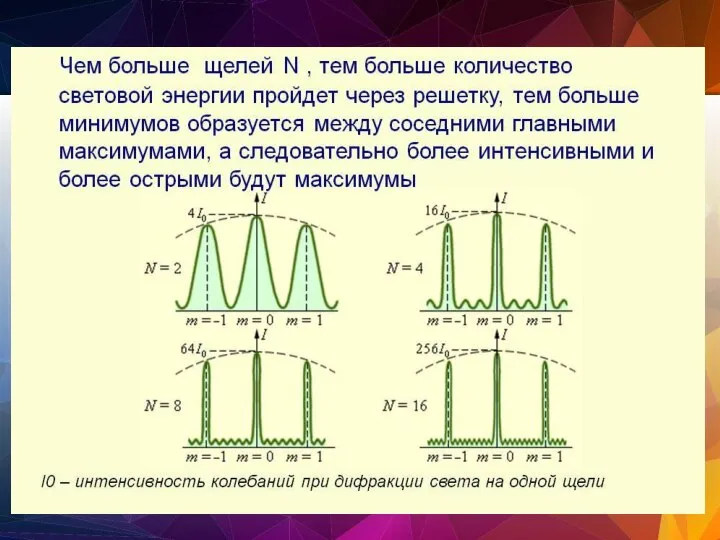
- 119. Дифракционная решетка
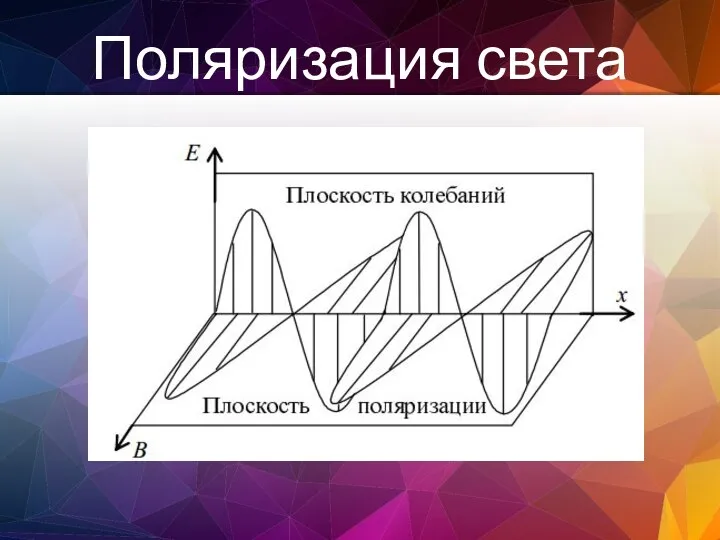
- 126. Поляризация света
- 127. Пусть монохроматическая волна распространяется вдоль оси х. Рассмотрим состояние векторов в некоторый момент времени. Векторы электрического
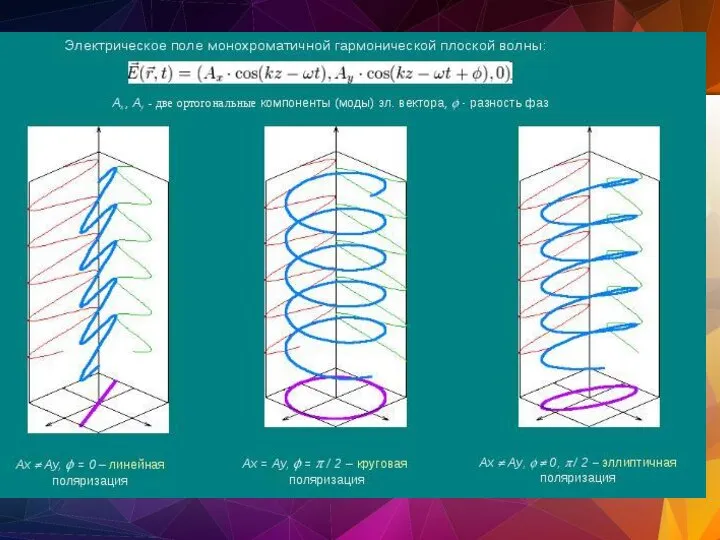
- 132. Циркулярно и линейно поляризованная плоская электромагнитная волна
- 134. Двойное лучепреломление
- 135. Особенностью таких кристаллов является то, что световые лучи с разными плоскостями поляризации имеют разные скорости внутри
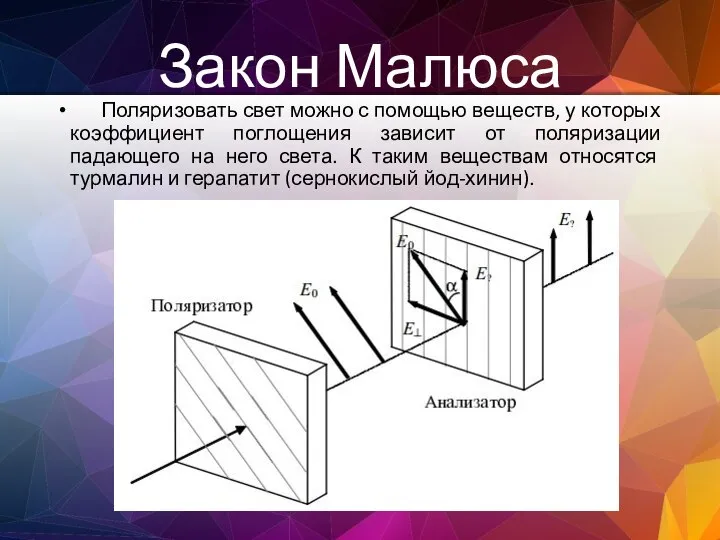
- 137. Закон Малюса Поляризовать свет можно с помощью веществ, у которых коэффициент поглощения зависит от поляризации падающего
- 138. Пусть на пластинку из турмалина или герапатита падает естественный свет. Свет, выходящий из пластинки, будет поляризован,
- 140. Закон Малюса
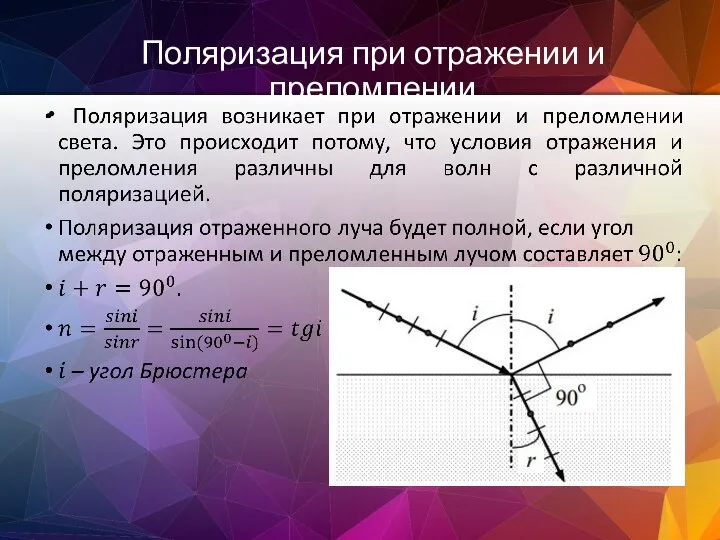
- 141. Поляризация при отражении и преломлении
- 142. Закон Брюстера
- 143. Вращение плоскости поляризации Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через
- 145. Приборы, использующие этот принцип называются сахариметрами.
- 146. Физический смысл спектрального разложения.
- 147. Известно, что произвольное немонохроматическое волновое возмущение можно представить в виде суперпозиции волн или, как говорят, разложить
- 148. Тепловое излучение - Свечение тел, обусловленное нагреванием. Тепловое излучение , является самым распространенным в природе, совершается
- 149. Излучение абсолютно черного тела Абсолютно черное тело – это такое тело, которое поглощает все падающее на
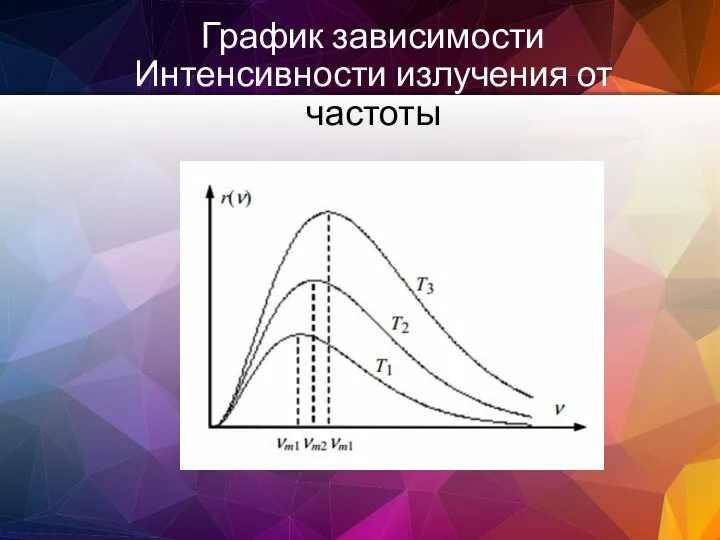
- 150. График зависимости Интенсивности излучения от частоты
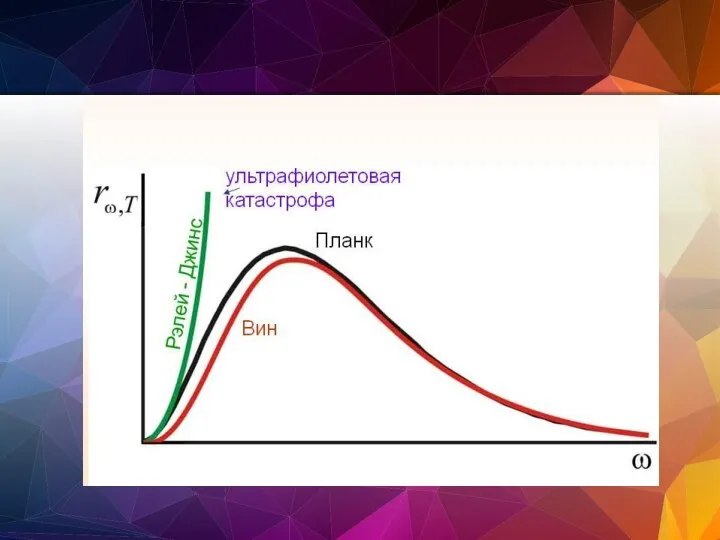
- 152. Закон смещения Вина Немецкий физик Вильгельм Вин в 1893 году, распространив понятие температуры и энтропии на
- 153. Гипотеза Планка
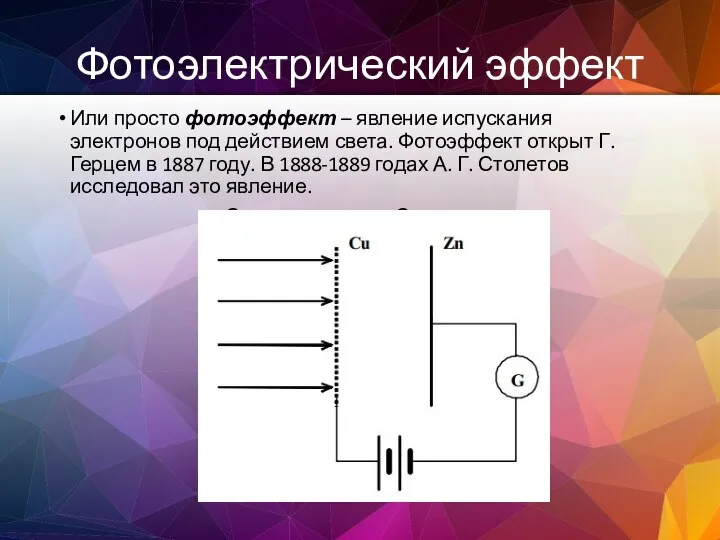
- 155. Фотоэлектрический эффект Или просто фотоэффект – явление испускания электронов под действием света. Фотоэффект открыт Г. Герцем
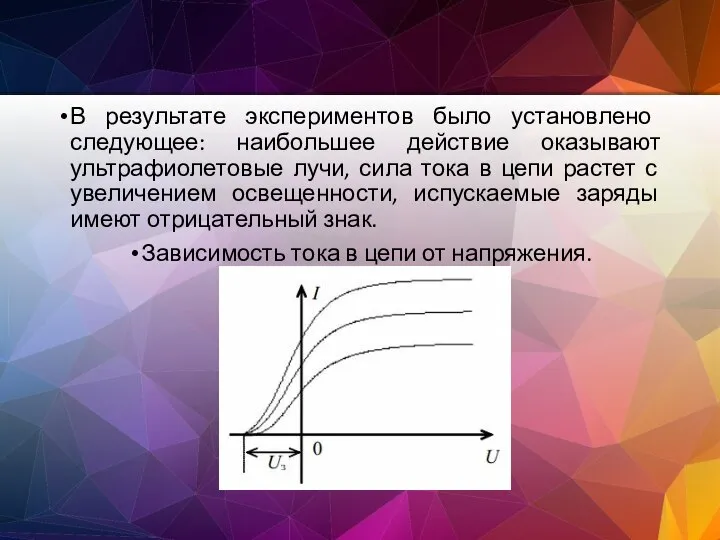
- 156. В результате экспериментов было установлено следующее: наибольшее действие оказывают ультрафиолетовые лучи, сила тока в цепи растет
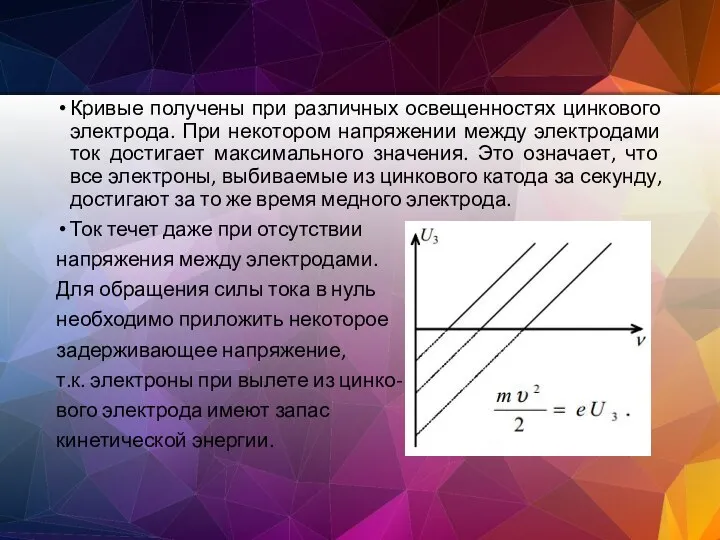
- 157. Кривые получены при различных освещенностях цинкового электрода. При некотором напряжении между электродами ток достигает максимального значения.
- 160. Скачать презентацию










































































































 Принципы автоматического управления пуском и торможением двигателя
Принципы автоматического управления пуском и торможением двигателя Решение задач по теме Прямолинейное равноускоренное движение
Решение задач по теме Прямолинейное равноускоренное движение Механические передачи
Механические передачи Взаимосвязь фундаментальных констант во Вселенной
Взаимосвязь фундаментальных констант во Вселенной Исследование закономерностей параллельного соединения проводников
Исследование закономерностей параллельного соединения проводников Путешествие по океану Знаний
Путешествие по океану Знаний Электрическое освещение бытовых и промышленных объектов
Электрическое освещение бытовых и промышленных объектов 1664775489323__ml7bfa (1)
1664775489323__ml7bfa (1) Перенос теплоты
Перенос теплоты Электризация тел. Электрический заряд. Закон сохранения электрического заряда
Электризация тел. Электрический заряд. Закон сохранения электрического заряда Использование энергии Солнца на Земле
Использование энергии Солнца на Земле Дифференцирующие и интегрирующие цепи
Дифференцирующие и интегрирующие цепи Реактивная сила
Реактивная сила Источники света. Распространение света
Источники света. Распространение света Магнитное поле
Магнитное поле Исследование воздействия волн на большие плавучие сооружения
Исследование воздействия волн на большие плавучие сооружения Первые рычаги
Первые рычаги Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Метрология
Метрология Магнитостатика. Магнитное поле
Магнитостатика. Магнитное поле Замена радиатора на системе охлаждения для марки ВАЗ 2107
Замена радиатора на системе охлаждения для марки ВАЗ 2107 Описание линейных дискретных систем в Zобласти. Тема № 8
Описание линейных дискретных систем в Zобласти. Тема № 8 Инфракрасное излучение
Инфракрасное излучение 00082e78-475de346
00082e78-475de346 Плоская электромагнитная волна. Лекция 2с 7 (2)
Плоская электромагнитная волна. Лекция 2с 7 (2) Изменение внутренней энергии газа в процессе теплообмена и совершения работы. Первое начало термодинамики. Лекция 5
Изменение внутренней энергии газа в процессе теплообмена и совершения работы. Первое начало термодинамики. Лекция 5 Аналогово-цифровой контроллер
Аналогово-цифровой контроллер Презентация на тему Агрегатное состояние вещества
Презентация на тему Агрегатное состояние вещества