Слайд 2Требования к выполненной работе:
Чертёж должен быть чётким, не мелким, примерно на треть

страницы, цифры написаны чертёжным шрифтом
Соблюдаем толщину основных толстых и тонких размерных линий
Не должно быть зачёркиваний, исправлений, пересечения размерных линий. Пользуйтесь штрихом или черновиками
В решении между строчками должен быть пробел
Оформление задачи: Дано, что сделать, решение, ответ.
Все единицы измерения должны быть проставлены.
Поясняющий текст к задаче ВЕСЬ записываем, без этого не выше тройки.
Слайд 3Критерии оценивания задачи
Оценка «отлично» выставляется при правильно решённой задаче: аккуратно и чисто,

в соответствии с требованиями, оформленном решении, при максимальной самостоятельности.
Оценка «хорошо» выставляется при правильно решенной задаче, при наличии в ходе решения незначительных исправлений и помарок, с подсказками преподавателя
Оценка «удовлетворительно» выставляется, если после проверки в работе будут исправлены все ошибки и она будет оформлена в соответствии с требованиями.
Во всех остальных случаях работа не засчитывается
Слайд 4Момент инерции
Величина, которая показывает, насколько трудно раскручивать (изгибать) тело относительно какой-либо оси,

проходящей через центр масс (тяжести)
Слайд 5Момент инерции сечения характеризует жёсткость
А) Чем больше момент инерции I, тем сложнее

прогнуть.
Б) Пример: линейка на прогиб: у нее сильно различается момент инерции вдоль осей.
Слайд 6Тела одинаковой массы могут вести себя по разному из-за распределения массы.
Момент инерции

учитывает это распределение.
При выборе конструкций среди различных сечений одинаковой площади выбирают сечение, которое будет лучше сопротивляться изгибу.
Слайд 71. Статический момент инерции -
алгебраическая сумма произведений:
элементарных площадей на
координаты их

центров тяжести
– мм3 , см3 , м3
(сумма d S ∙ х или d S ∙ у)
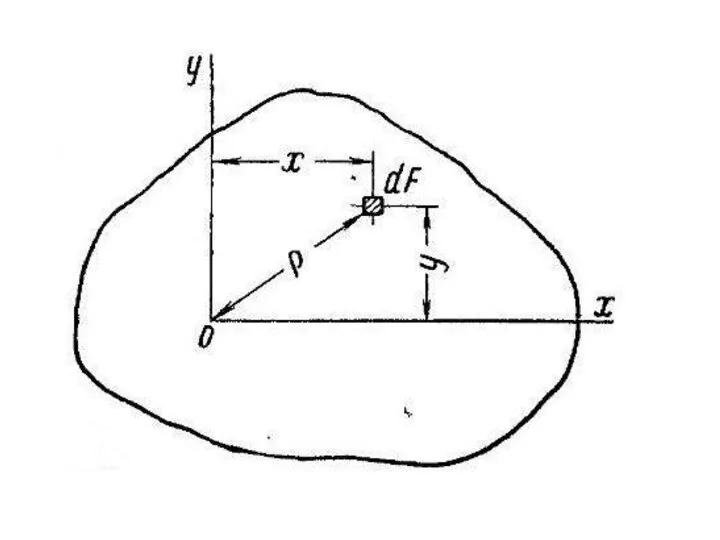
Слайд 9а) в интегральной форме
Sх = ∫ уdS - статический момент инерции

относительно оси х
Sу = ∫ хdS- статический момент инерции относительно оси у
Слайд 10
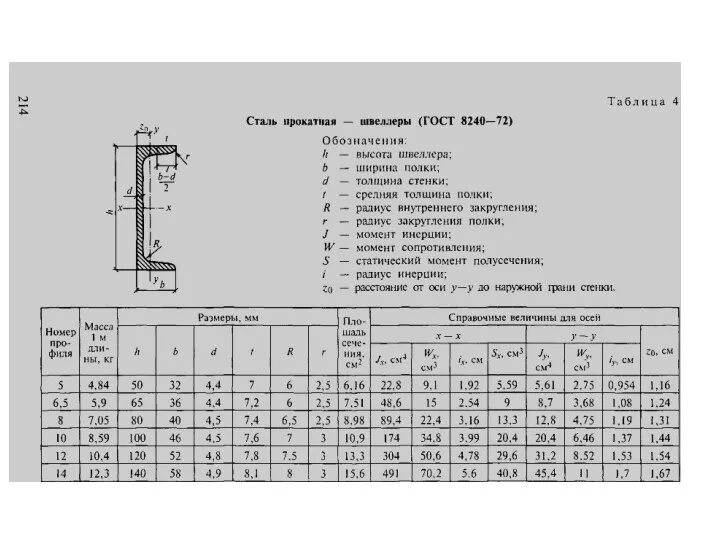
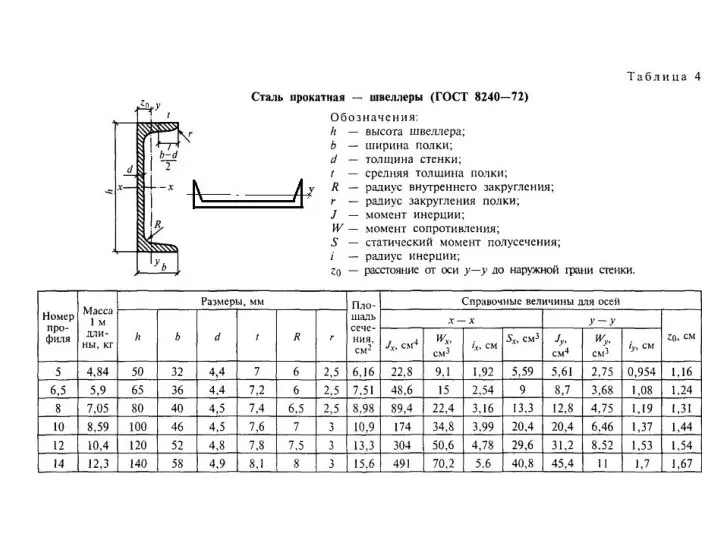
Задача № 9. «Определить главные моменты инерции заданного сечения из стандартных прокатных

профилей»
Слайд 12Последовательность решения задачи:
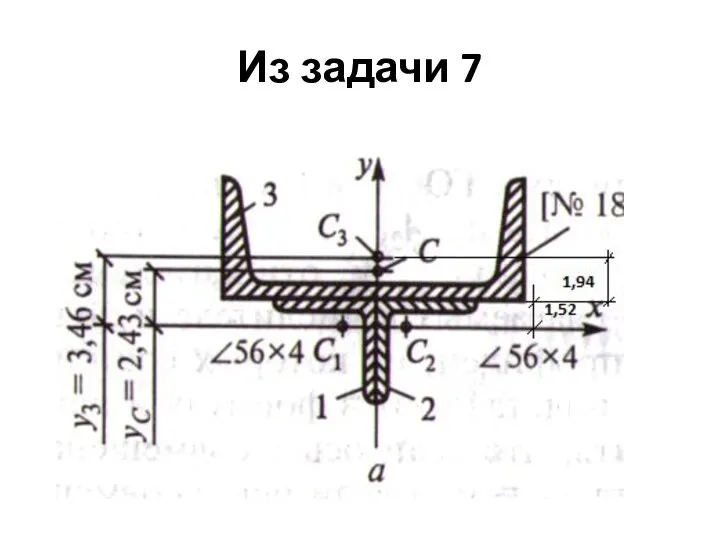
1. Положение центра тяжести определено в задаче 7, Ус =

2,43 см, если ось проходит через центр тяжести швеллера.
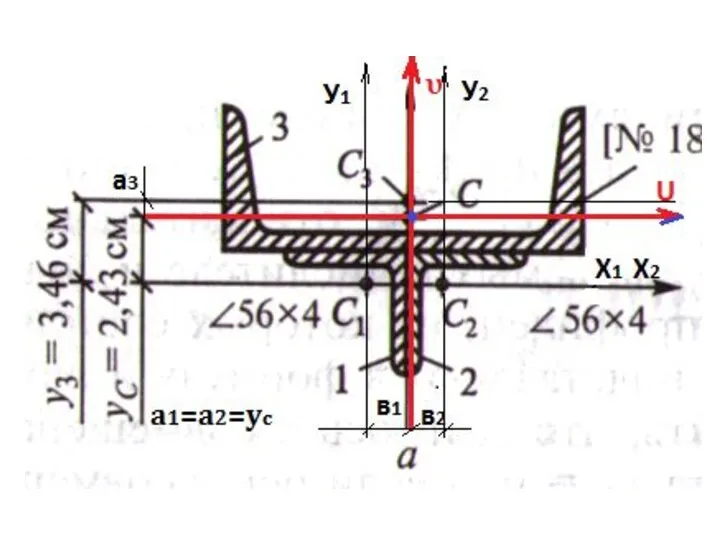
3. Провести центральные оси х1 х2 х3 у1 у2 у3
через центры тяжести С1 С2 С3
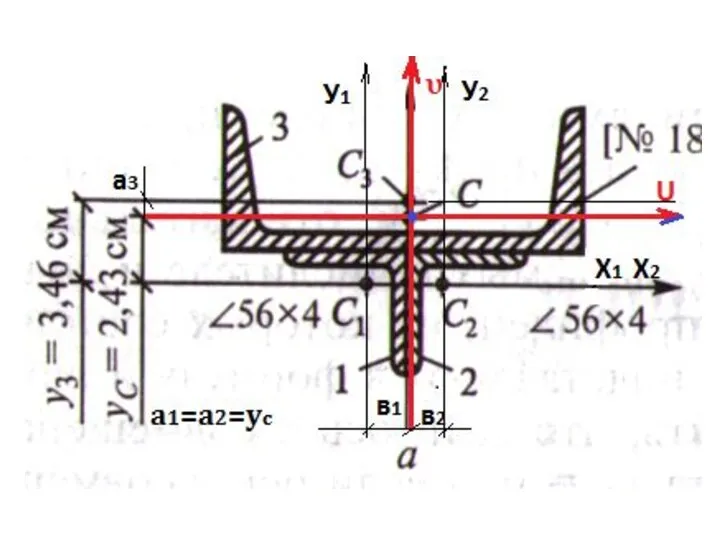
4. Провести главные центральные оси Х и У через центр тяжести С
А) вертикальную ось V совмещаем с осью симметрии
Б) горизонтальную u проводим через центр тяжести С перпендикулярно оси V
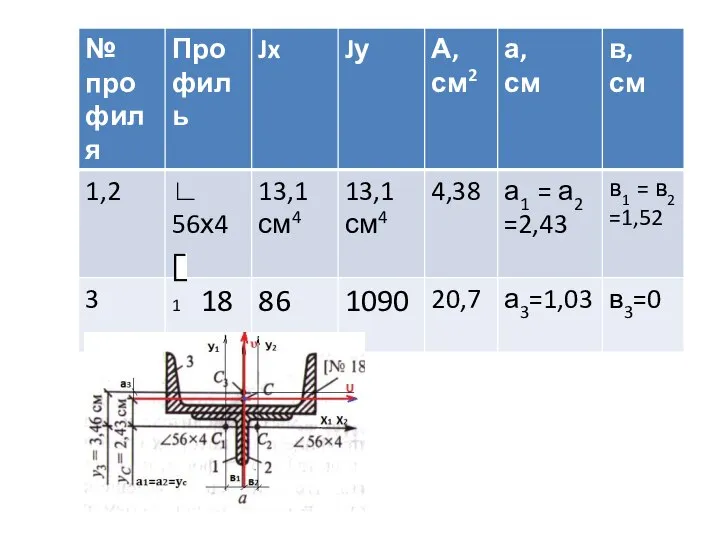
Слайд 145. Составить таблицу и занести в неё данные для определения главных моментов

инерции относительно главных центральных осей.
Слайд 16а1 – расстояние по вертикали от центра тяжести с1 до Главного центра

тяжести С (пересечения Главных центральных осей)
- КАК ПРАВИЛО, ЭТО Ус
а2 – от с2 до С
а3 – от с3 до С
а4 – от с4 до С
b1 – расстояние по горизонтали от центра тяжести с1 до Главного центра тяжести С (пересечения Главных центральных осей)
b 2 – от с2 до С
b 3 – от с3 до С
b 4 – от с4 до С
Слайд 236. Определить по формуле главный момент инерции относительно главной центральной оси u
7.

Определить по формуле главный момент инерции относительно главной центральной оси v
Слайд 24
6. Определим момент инерции сечения относительно оси u:
Ju = Juшв + Juуг

+ Juуг
А) так как уголки одинаковые и расположены на одинаковом расстоянии от оси u:
Ju = Juшв + 2·Juуг
Слайд 25
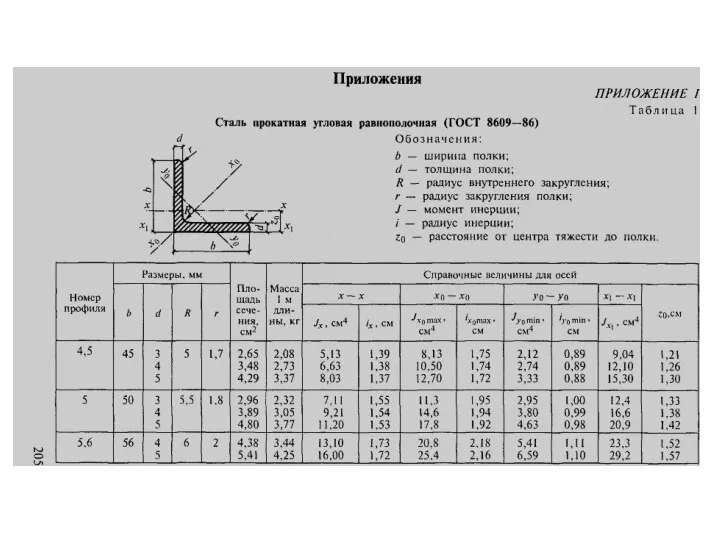
Б) момент инерции уголка № 56 х 4 относительно оси u:
Juшв =

Jx1шв + а12 ·Ауг = 13,1 + 2,432·4,38 = 39 см4
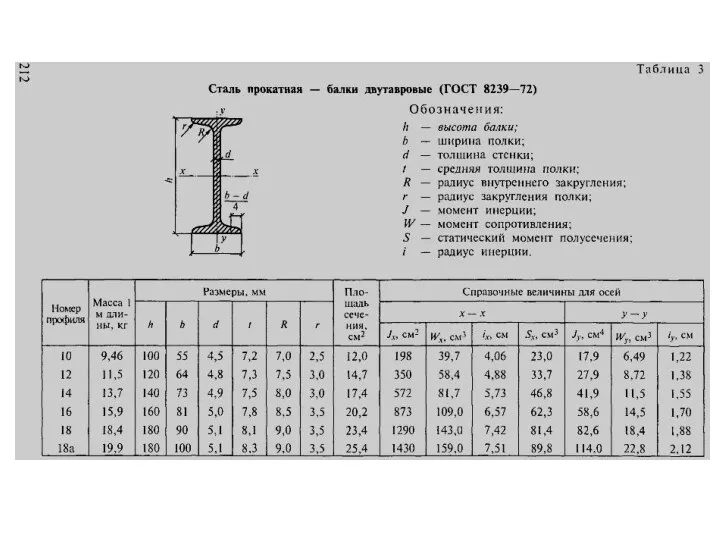
В) момент инерции швеллера № 18 относительно оси u:
Juшв = Jx1шв + а32 ·Ашв = 86 + 1,032 · 20,7 = 108 см4
Г) момент инерции сечения относительно оси u:
Ju =39 + 2· 108 = 255 см4
Слайд 26
7. Определим момент инерции сечения относительно оси V:
Jv = Jvшв + Jvуг

+ Jvуг
А) так как уголки одинаковые и расположены на одинаковом расстоянии от оси v:
Jv = Jvшв + 2·Jvуг















 Закон Ампера. Применение
Закон Ампера. Применение Параметры эвольвентного зубчатого зацепления
Параметры эвольвентного зубчатого зацепления Волновые процессы
Волновые процессы Плотность вещества. Решение задач
Плотность вещества. Решение задач Уровни описания технических систем
Уровни описания технических систем Техническое обслуживание и ремонт заднего моста автомобиля ГАЗ 31105. Экзаменационная работа
Техническое обслуживание и ремонт заднего моста автомобиля ГАЗ 31105. Экзаменационная работа Презентация на тему Постоянные магниты. Магнитное поле Земли
Презентация на тему Постоянные магниты. Магнитное поле Земли  Гидродинамика
Гидродинамика Розробка, виготовлення, випробування та комерціалізація біотеплогенератора потужністю 20 - 50 квт з термоелектричним модулем
Розробка, виготовлення, випробування та комерціалізація біотеплогенератора потужністю 20 - 50 квт з термоелектричним модулем Презентация на тему Тепловые двигатели 10 класс
Презентация на тему Тепловые двигатели 10 класс  Электрические явления. Заряд
Электрические явления. Заряд Проблемы применения нанотехнологии
Проблемы применения нанотехнологии Магнитная индукция
Магнитная индукция Методика организации лабораторных и экспериментальных работ учащихся на уроках физики
Методика организации лабораторных и экспериментальных работ учащихся на уроках физики Динамика. Первый закон Ньютона
Динамика. Первый закон Ньютона Потенциальное силовое поле
Потенциальное силовое поле Графен – бұл кәдімгі алмаз бен графиттен
Графен – бұл кәдімгі алмаз бен графиттен Критерии прочности при изгибе. Распространение критериев прочности на случай циклического нагружения
Критерии прочности при изгибе. Распространение критериев прочности на случай циклического нагружения Изменение импульса механической системы
Изменение импульса механической системы Презентация на тему Реактивное движение и его применение в технике
Презентация на тему Реактивное движение и его применение в технике  Асинхронные двигатели
Асинхронные двигатели Исследование одномерной схемы Йе на устойчивость
Исследование одномерной схемы Йе на устойчивость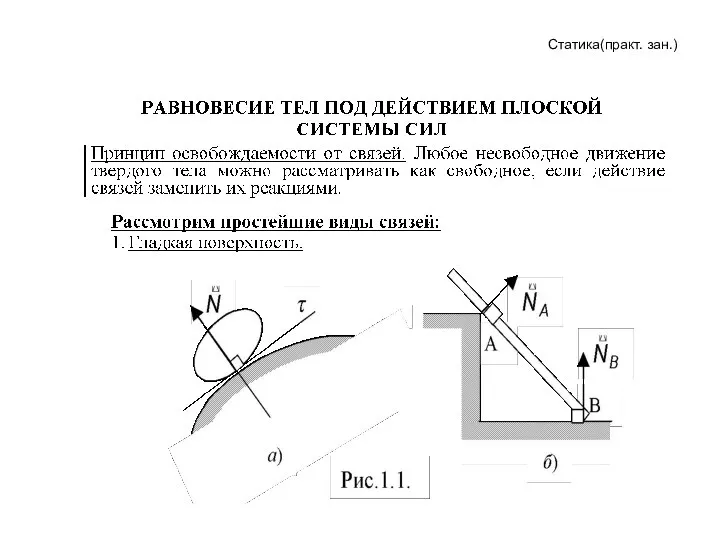 Равновесие тел под действием плоской системы сил
Равновесие тел под действием плоской системы сил Графен. Классические и квантовые низкоразмерные системы. Ковалентная химическая связь: σ- и π-электроны
Графен. Классические и квантовые низкоразмерные системы. Ковалентная химическая связь: σ- и π-электроны Научная лаборатория. Рассказ о профессии физик-химик
Научная лаборатория. Рассказ о профессии физик-химик Основы квантовой физики. Лекция 8
Основы квантовой физики. Лекция 8 Электроосветительные приборы
Электроосветительные приборы Презентация на тему Линзы
Презентация на тему Линзы