Содержание
- 2. Естественный и поляризованный свет Следствием теории Максвелла является поперечность световых волн: векторы напряженностей электрического Е и
- 3. Естественный и поляризованный свет Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы же излучают световые
- 4. Естественный и поляризованный свет Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!)
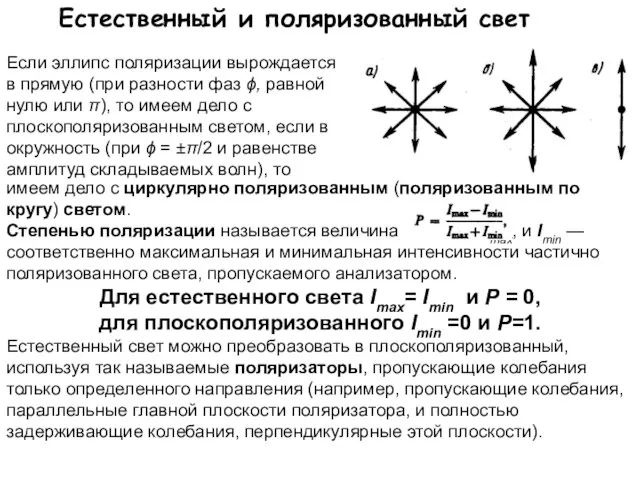
- 5. Естественный и поляризованный свет Если эллипс поляризации вырождается в прямую (при разности фаз ϕ, равной нулю
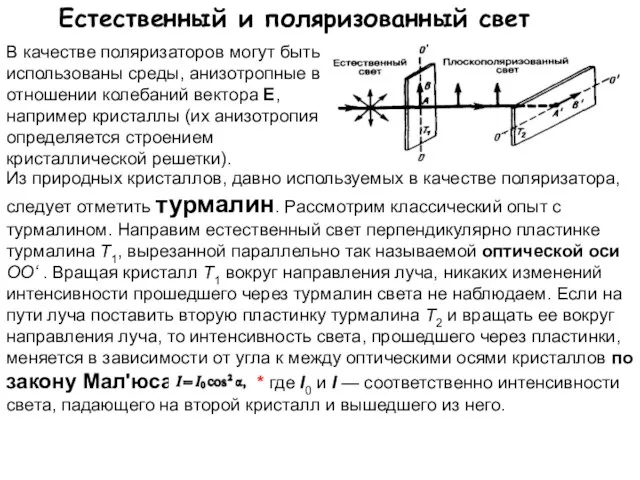
- 6. Естественный и поляризованный свет В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора
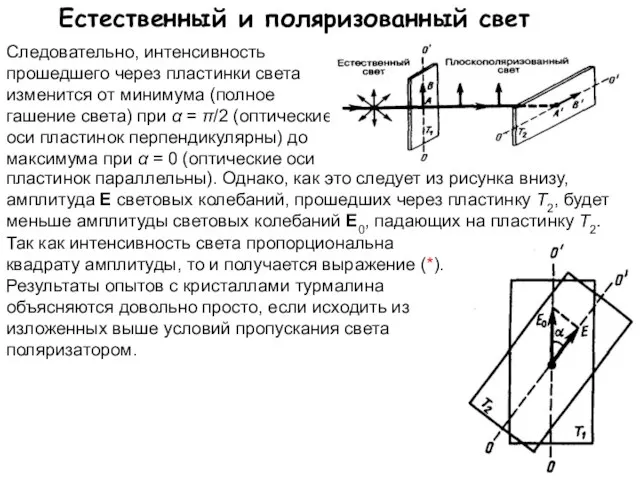
- 7. Естественный и поляризованный свет Следовательно, интенсивность прошедшего через пластинки света изменится от минимума (полное гашение света)
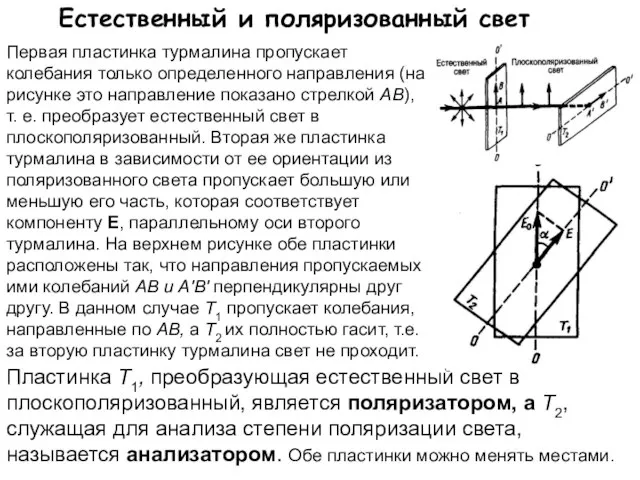
- 8. Естественный и поляризованный свет Пластинка Т1, преобразующая естественный свет в плоскополяризованный, является поляризатором, а Т2, служащая
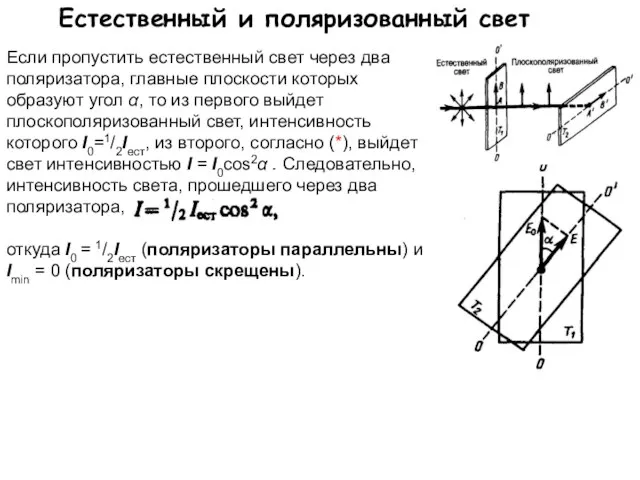
- 9. Естественный и поляризованный свет Если пропустить естественный свет через два поляризатора, главные плоскости которых образуют угол
- 10. Поляризация света при отражении и преломлении на границе двух диэлектриков Если естественный свет падает на границу
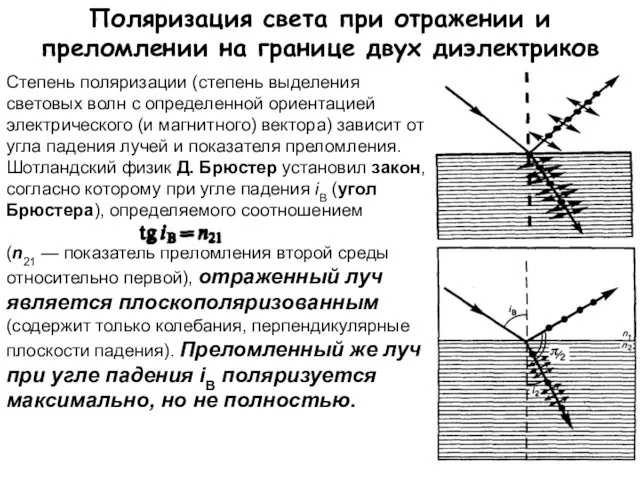
- 11. Поляризация света при отражении и преломлении на границе двух диэлектриков Степень поляризации (степень выделения световых волн
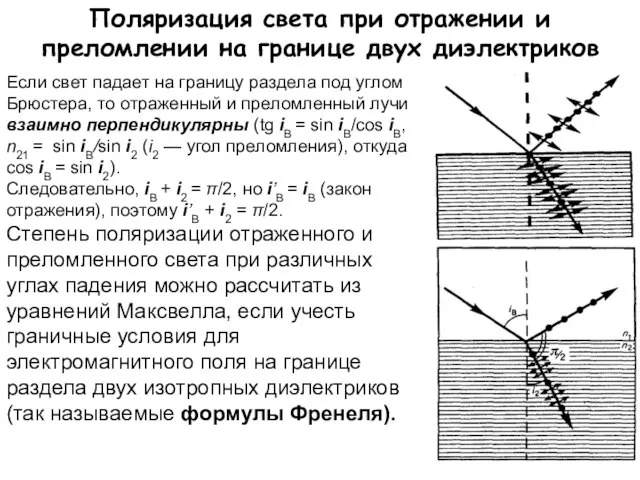
- 12. Поляризация света при отражении и преломлении на границе двух диэлектриков Если свет падает на границу раздела
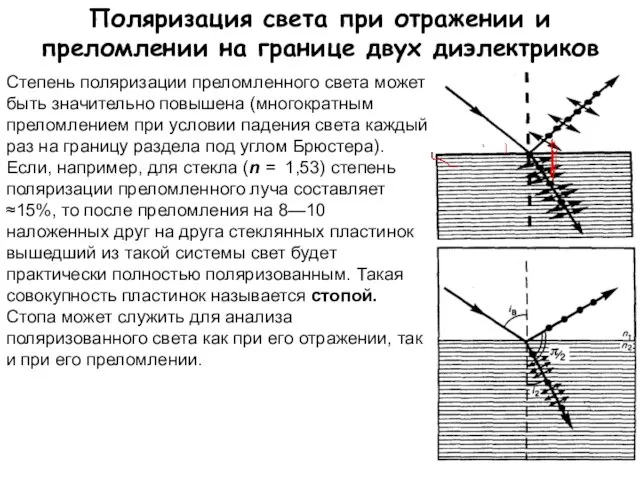
- 13. Поляризация света при отражении и преломлении на границе двух диэлектриков Степень поляризации преломленного света может быть
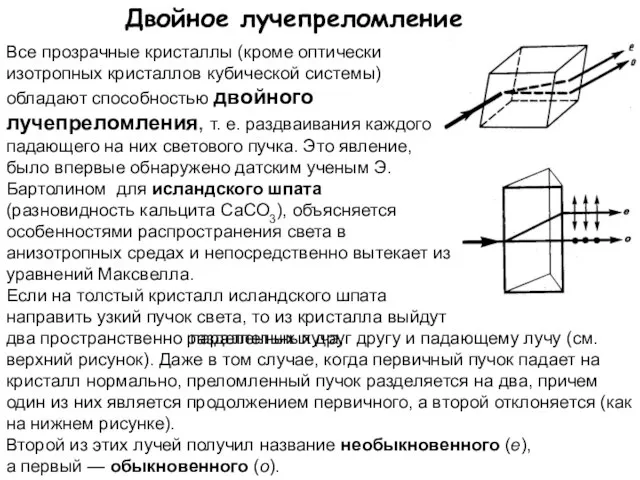
- 14. Двойное лучепреломление Все прозрачные кристаллы (кроме оптически изотропных кристаллов кубической системы) обладают способностью двойного лучепреломления, т.
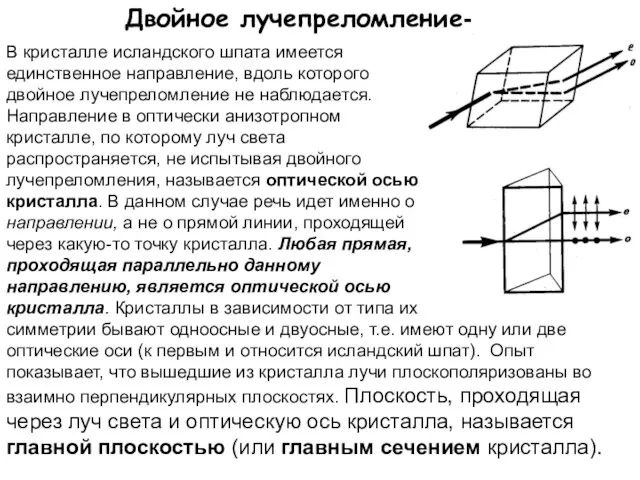
- 15. Двойное лучепреломление- В кристалле исландского шпата имеется единственное направление, вдоль которого двойное лучепреломление не наблюдается. Направление
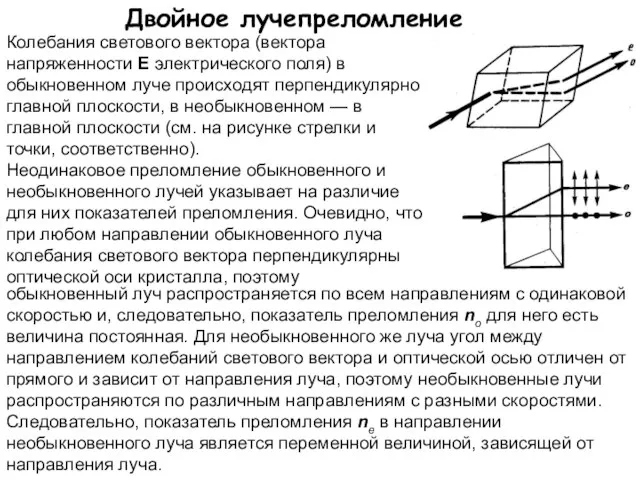
- 16. Двойное лучепреломление Колебания светового вектора (вектора напряженности Е электрического поля) в обыкновенном луче происходят перпендикулярно главной
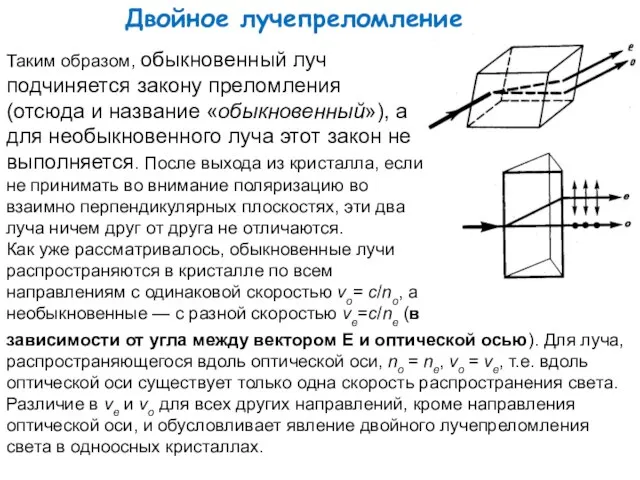
- 17. Двойное лучепреломление Таким образом, обыкновенный луч подчиняется закону преломления (отсюда и название «обыкновенный»), а для необыкновенного
- 18. Двойное лучепреломление Допустим, что в точке S внутри одноосного кристалла находится точечный источник света. На рисунке
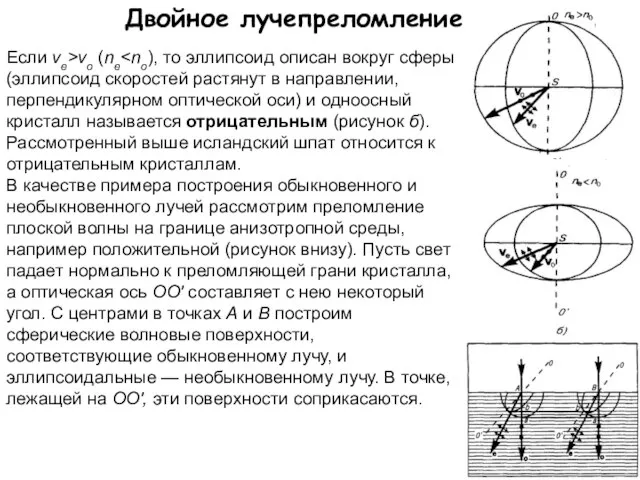
- 19. Двойное лучепреломление Если ve>vo (ne В качестве примера построения обыкновенного и необыкновенного лучей рассмотрим преломление плоской
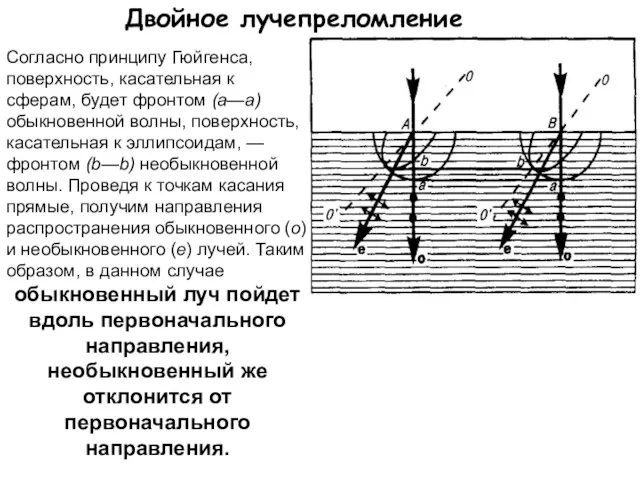
- 20. Двойное лучепреломление Согласно принципу Гюйгенса, поверхность, касательная к сферам, будет фронтом (а—а) обыкновенной волны, поверхность, касательная
- 21. Поляризационные призмы и поляроиды В основе работы поляризационных приспособлений, служащих для получения поляризованного света, лежит явление
- 22. Поляризационные призмы и поляроиды Типичным представителем поляризационных призм является призма Н`иколя, называемая часто н`иколем. Призма Николя
- 23. Поляризационные призмы и поляроиды Двоякопреломляющие призмы используют различие в показателях преломления обыкновенного и необыкновенного лучей, чтобы
- 24. Поляризационные призмы и поляроиды Двоякопреломляющие кристаллы обладают свойством дихроизма, т. е. различного поглощения света в зависимости
- 25. Поляризационные призмы и поляроиды Преимущество поляроидов перед призмами — возможность изготовлять их с площадями поверхностей до
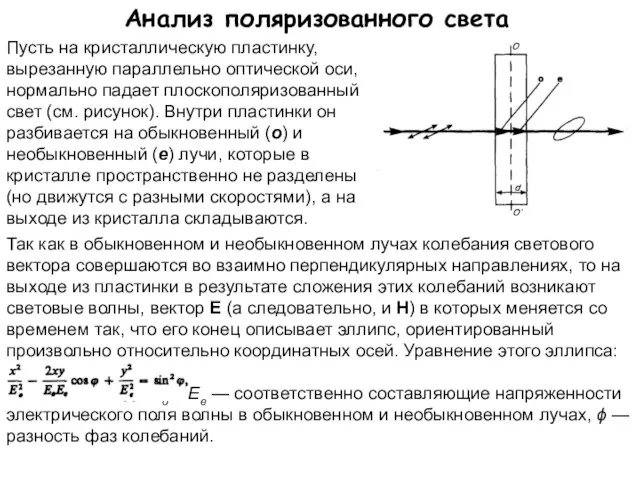
- 26. Анализ поляризованного света Пусть на кристаллическую пластинку, вырезанную параллельно оптической оси, нормально падает плоскополяризованный свет (см.
- 27. Анализ поляризованного света Таким образом, в результате прохождения через кристаллическую пластинку плоскополяризованный свет превращается в эллиптически
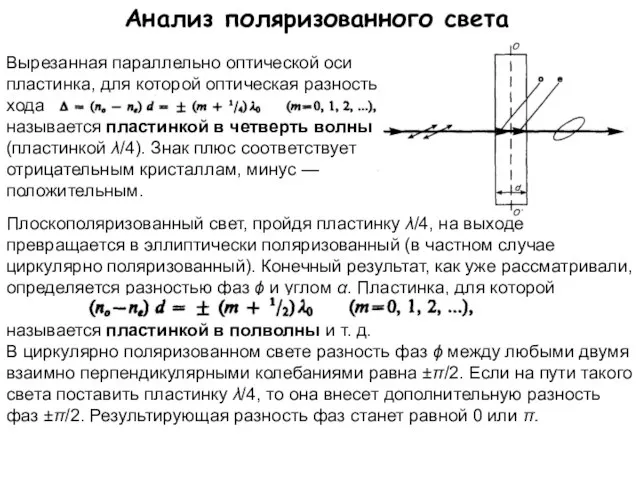
- 28. Анализ поляризованного света Вырезанная параллельно оптической оси пластинка, для которой оптическая разность хода называется пластинкой в
- 29. Анализ поляризованного света Следовательно (см. (*)), циркулярно поляризованный свет, пройдя пластинку λ/4, становится плоскополяризованным. Если теперь
- 30. Искусственная оптическая анизотропия Двойное лучепреломление имеет место в естественных анизотропных средах. Существуют, однако, различные способы получения
- 31. Искусственная оптическая анизотропия Мерой возникающей оптической анизотропии служит разность показателей преломления обыкновенного и необыкновенного лучей в
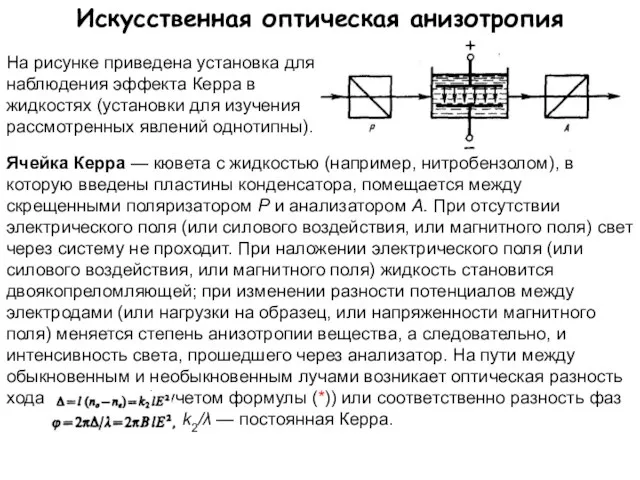
- 32. Искусственная оптическая анизотропия На рисунке приведена установка для наблюдения эффекта Керра в жидкостях (установки для изучения
- 33. Искусственная оптическая анизотропия Эффект Керра — оптическая анизотропия веществ под действием электрического поля — объясняется различной
- 34. Вращение плоскости поляризации Некоторые вещества (например, из твердых тел — кварц, сахар, киноварь, из жидкостей —
- 35. Вращение плоскости поляризации Опыт показывает, что угол поворота плоскости поляризации для оптически активных кристаллов и чистых
- 36. Вращение плоскости поляризации Оптически активные вещества в зависимости от направления вращения плоскости поляризации разделяются на право-
- 38. Скачать презентацию


















 Соединение обмоток генератора треугольником
Соединение обмоток генератора треугольником Мимеография
Мимеография Велосипед: из чего состоит и его характеристики
Велосипед: из чего состоит и его характеристики Презентация на тему Теория фотоэффекта
Презентация на тему Теория фотоэффекта  Жидкие кристаллы
Жидкие кристаллы Телескопы
Телескопы Излучение электромагнитного поля. Антенны
Излучение электромагнитного поля. Антенны Чистые источники энергии. Выполнила: учитель физики ГБОУ ЦО «Школа здоровья» №628 Лисицкая Елена Владимировна
Чистые источники энергии. Выполнила: учитель физики ГБОУ ЦО «Школа здоровья» №628 Лисицкая Елена Владимировна Тест по теме Архимедова сила. Плавание тел
Тест по теме Архимедова сила. Плавание тел Метрология ионизирующих излучений. (Лекция 3)
Метрология ионизирующих излучений. (Лекция 3) Телефон без электричества. Физика
Телефон без электричества. Физика Механика. Законы сохранения в механике
Механика. Законы сохранения в механике Презентация на тему Простые механизмы
Презентация на тему Простые механизмы  Решение задач по теме Электрический ток
Решение задач по теме Электрический ток Метод рефрактометрии и ИК-спектроскопии
Метод рефрактометрии и ИК-спектроскопии Урок 7
Урок 7 Величайшие открытия физики
Величайшие открытия физики Тепловые двигатели
Тепловые двигатели Расчет давления и атомных напряжений в МД
Расчет давления и атомных напряжений в МД Сообщающиеся сосуды. 7 класс
Сообщающиеся сосуды. 7 класс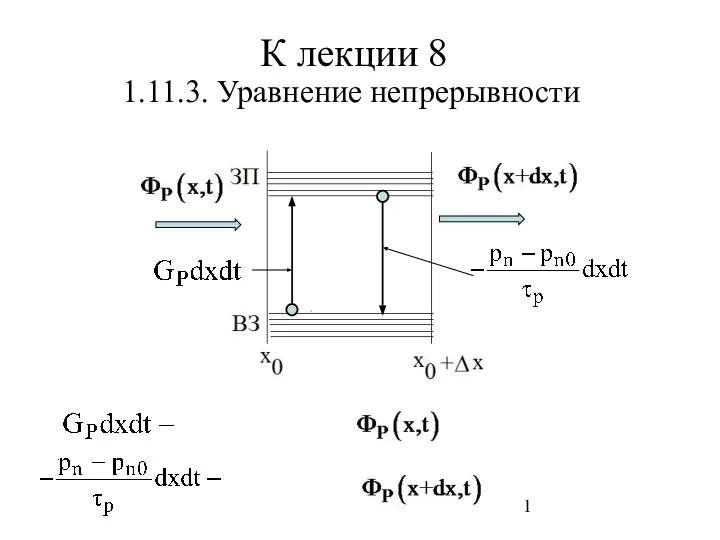 Уравнение непрерывности
Уравнение непрерывности Термодинамика
Термодинамика Коллективные спасательные средства. Тема 2.3
Коллективные спасательные средства. Тема 2.3 Лекция 7. Расчет статически неопределимых систем методом сил
Лекция 7. Расчет статически неопределимых систем методом сил Практическое занятие. Расчет тока КЗ
Практическое занятие. Расчет тока КЗ Последовательное и параллельное соединения проводников
Последовательное и параллельное соединения проводников Электрические силы
Электрические силы Движение. Тело отсчёта
Движение. Тело отсчёта