Слайд 21. Основные понятия.
1.1. Тепловое движение, термодинамические системы, молярная масса.
Все тела в природе

состоят из частиц – атомов или молекул. Эти частицы движутся, и их движение подчиняется законам механики (классической или квантовой). Поэтому для строгого описания их движения можно было бы для каждой частицы написать второй закон Ньютона и решить получившуюся систему уравнений.
Progr D: Progr E: Progr F: Progr G: Progr H:
Слайд 3Невозможность детального описания поведения молекул.
Однако число частиц в реальных телах равно около

1026 штук, и число уравнений Ньютона было бы того же порядка. Решить такую систему уравнений нельзя даже в принципе. Поэтому для описания систем из большого числа частиц, таких как реальные тела, используют энергетический способ.
Слайд 4Хаотичность движения молекул.
Это означает, что изначально отказываются от необходимости детально описать движение

каждой частицы, а лишь найти энергии этих частиц, да и то не каждой, а лишь среднюю энергию. Благодаря большому числу частиц, их движение приобретает качественно новое свойство, не изучаемое в механике – оно становится абсолютно беспорядочным, хаотическим.
Progr D: Progr E: Progr F: Progr G: Progr H:
Слайд 5Термодинамическая система.
Определение. Беспорядочное, хаотическое движение частиц реальных тел называется тепловым движением.
Определение. Часть

физики, изучающая тепловое движение называется термодинамикой.
Определение. Любая система, свойства которой определяются тепловым движением, называется термодинамической системой.
Слайд 6Количество вещества.
Поведение т.д.с. зависит в первую очередь от количества вещества, т.е. от

количества частиц в системе. Единицей измерения количества вещества можно было бы выбрать одну частицу, но это слишком малая единица, и пришлось бы использовать в уравнениях числа с большими порядками.
Слайд 7Единица измерения количества вещества.

Слайд 8Формула количества вещества.

Слайд 101.2. Термодинамические параметры. Уравнение состояния ТДС.
Определение. Параметры, описывающие состояние термодинамической системы, называются

термодинамическими параметрами.
Слайд 11Средняя кинетическая энергия молекул

Слайд 15Объём ТДС.
На поведение термодинамической системы оказывает влияние и объём пространства, который она

занимает. Таким образом, температура, давление и объём – основные параметры, описывающие поведение термодинамической системы.
Слайд 16Термодинамическое равновесие.
Характерной особенностью всех термодинамических систем является тот факт, что представленные самим

себе они всегда стремятся к т.н. термодинамическому равновесию.
Определение. Говорят, что термодинамическая система находится в состоянии термодинамического равновесия, если все её термодинамические параметры в отсутствии внешнего воздействия остаются постоянными сколь угодно долго.
Progr D: Progr E: Progr F: Progr G: Progr H:
Слайд 17Термодинамика неравновесных процессов.
Если термодинамическая система не находится в равновесии, её параметры могут

иметь разные значения в разных точках. Такие состояния изучает термодинамика неравновесных процессов.
Слайд 18Связь между термодинамическими параметрами.
Разным равновесным состояниям системы отвечают, вообще говоря, разные параметры.

Однако, изменяться параметры не могут независимо. Изменение одних параметров обязательно приводит к соответствующему изменению других. С математической точки зрения это означает, что между параметрами, описывающими одну и ту же термодинамическую систему существует функциональную связь.
Слайд 20Уравнения состояний в явном виде.

Слайд 21Термодинамический процесс.
Определение. Говорят, что система находится в термодинамическом процессе, если не все

её параметры остаются с течением времени постоянными.
Протекание процесса, кроме уравнения состояния ТДС, подчиняется некоторому дополнительному условию, называемому условием процесса.
Определение.
Уравнение состояния ТДС при выполнении условия процесса называется уравнением процесса.
Слайд 24Связь частных производных термодинамических параметров друг по другу.

Слайд 252. Основы термодинамики. Газовые законы.
2.1. Основное уравнение МКТ.
Определение температуры через среднюю кинетическую

энергию молекул требует знания кинетической энергии молекул, что непосредственным измерением сделать нельзя. Поэтому такое определение было бы бесполезно, если бы не было возможности косвенно определять кинетическую энергию молекул через макроскопические параметры систем. А именно, средняя кинетическая энергия молекул связана, как оказывается, с давлением.
Слайд 29Давление, оказываемое на стенку.

Слайд 31Проверка основного уравнения МКТ
Progr D: Progr E: Progr F: Progr G: Progr

H:
Слайд 322.2. Законы идеального газа.
Определение. Идеальным газом называется газ, частицы которого представляют собой

материальные точки и взаимодействуют между собой только в момент столкновения.
Слайд 34Проверка
Progr D: Progr E: Progr F: Progr G: Progr H:

Слайд 35Связь давления, объёма и температуры.

Слайд 36Универсальная газовая постоянная.

Слайд 37Уравнение Менделеева-Клапейрона.

Слайд 38Проверка уравнения Менделеева-Клапейрона.
Progr D: Progr E: Progr F: Progr G: Progr H:

Слайд 39Изопроцессы.
Из него следуют уравнения всех основных изопроцессов идеального газа.
Определение. Изопроцессами называются такие

процессы, при которых один из термодинамических параметров остаётся неизменным.
Слайд 40Уравнение Гей-Люссака или изобарический процесс.

Слайд 41Проверка закона Гей-Люссака
Progr D: Progr E: Progr F: Progr G: Progr H:

Слайд 42Один из способов измерения температуры.
Этот процесс называется изобарическим или законом Гей-Люссака. Графиком

этой зависимости является прямая линия. Из этого закона следует, что при объём газа тоже должен стать равным нулю.
На этом равенстве основан один из самых распространённых способов измерения температуры. Достаточно померить объём газа и по уравнению Гей-Люссака можно найти температуру.
Слайд 43Закон Шарля, изохорический процесс.

Слайд 44Проверка закона Шарля.
Progr D: Progr E: Progr F: Progr G: Progr H:

Слайд 45Изотермический процесс, закон Бойля-Мариотта.













































 Модели строения атома
Модели строения атома Принцип работы фотоаппарата
Принцип работы фотоаппарата Презентация на тему Действие магнитного поля на проводники с током (11 класс)
Презентация на тему Действие магнитного поля на проводники с током (11 класс)  Первичные и вторичные параметры длинной линии. Лекция Д1
Первичные и вторичные параметры длинной линии. Лекция Д1 Prezentatsia_para_sil
Prezentatsia_para_sil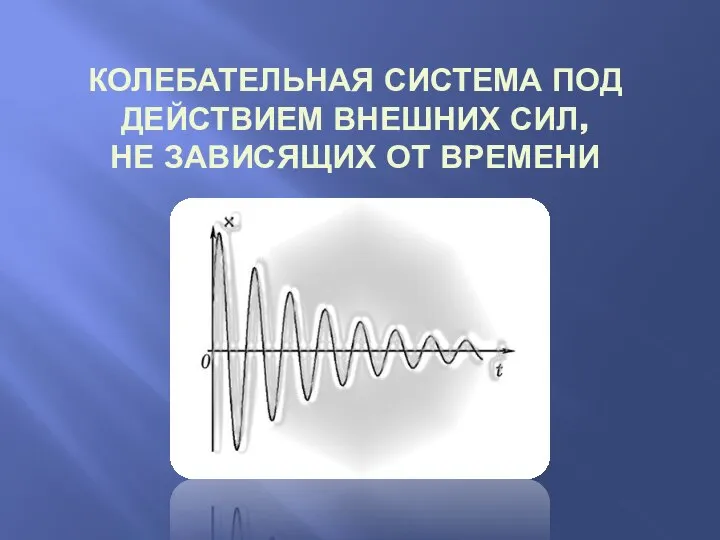 Колебательная система под действием внешних сил, не зависящих от времени
Колебательная система под действием внешних сил, не зависящих от времени Теория распределенной линии передачи. Эквивалентная схема отрезка линии передачи
Теория распределенной линии передачи. Эквивалентная схема отрезка линии передачи Марковские процессы. Правило
Марковские процессы. Правило Виды излучений
Виды излучений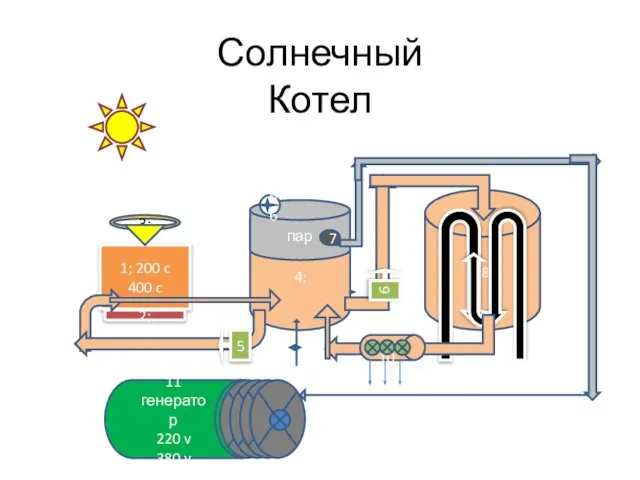 Солнечный котел
Солнечный котел Механические передачи. Цилиндрические и конические зубчатые передачи. (Лекция 5)
Механические передачи. Цилиндрические и конические зубчатые передачи. (Лекция 5) Вторичные (гидродинамические) МУН. Лекция 4-5
Вторичные (гидродинамические) МУН. Лекция 4-5 Взаимные превращения жидкостей и газов
Взаимные превращения жидкостей и газов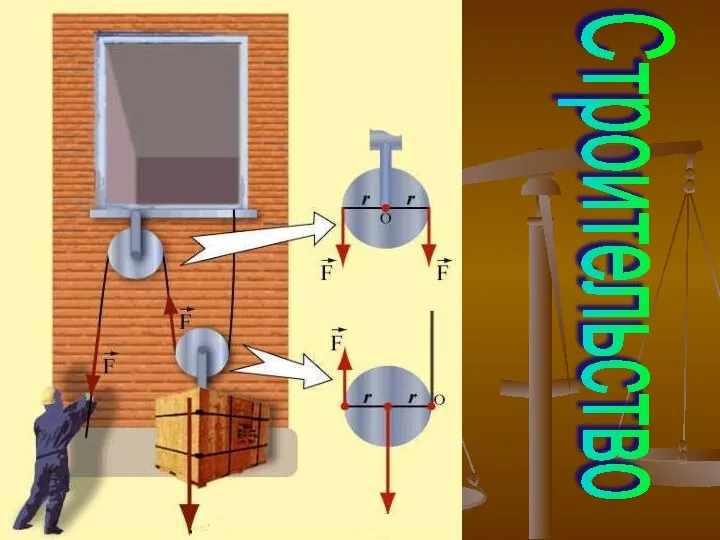 Наклонная плоскость
Наклонная плоскость Ядерные реакции. Атом, атомное ядро, атомная энергия (Лекция 2)
Ядерные реакции. Атом, атомное ядро, атомная энергия (Лекция 2) Система пуска двигателя
Система пуска двигателя Саха теңдеуі
Саха теңдеуі The nanoengineering
The nanoengineering Развитие ракетной техники
Развитие ракетной техники Законы сохранения в механике
Законы сохранения в механике Магнитные поля
Магнитные поля "Масса тела. Плотность вещества".
"Масса тела. Плотность вещества". Явление фотоэффекта
Явление фотоэффекта Светодиодная лампа. Открытый городской конкурс научно-технических проектов школьников Инженерный старт – 2019
Светодиодная лампа. Открытый городской конкурс научно-технических проектов школьников Инженерный старт – 2019 Лекция 5_Физики_Основы термодинамики (1)
Лекция 5_Физики_Основы термодинамики (1) Снежные причуды. Всё о снеге и снежинках
Снежные причуды. Всё о снеге и снежинках Обработка деталей на оборудовании с ЧПУ
Обработка деталей на оборудовании с ЧПУ Методические указания к курсовому проекту по спецкурсу № 2. Теории ядерных реакторов
Методические указания к курсовому проекту по спецкурсу № 2. Теории ядерных реакторов