Содержание
- 2. Понимать означает всегда только одно: познавать взаимосвязи… В. Гейзенберг В физике… нет места для путаных мыслей…
- 3. А.С. Чуев - 2020
- 4. Аналогия – вращение воды в сливающейся ванне. А.С. Чуев - 2020 Вихревое электрическое поле
- 5. Для электростатического поля: Согласно принципу суперпозиции: А.С. Чуев - 2020
- 6. Теорема Стокса Вихревое электрическое поле возникает при изменении магнитного поля Закон Фарадея А.С. Чуев - 2020
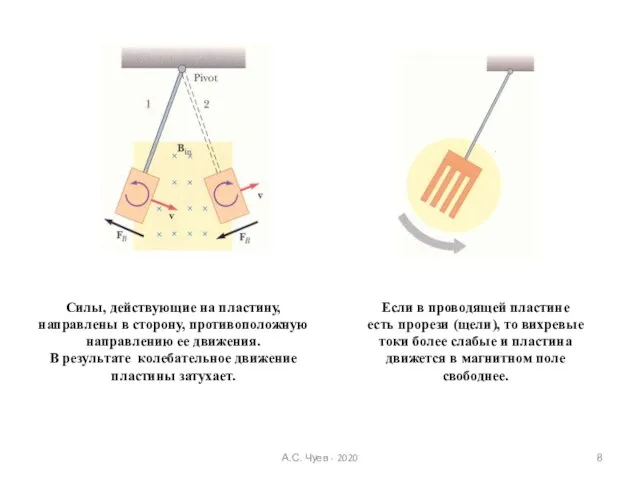
- 7. Токи Фуко. Переменный магнитный поток индуцирует ЭДС и ток в контуре. Эти токи являются результатом перемещения
- 8. Силы, действующие на пластину, направлены в сторону, противоположную направлению ее движения. В результате колебательное движение пластины
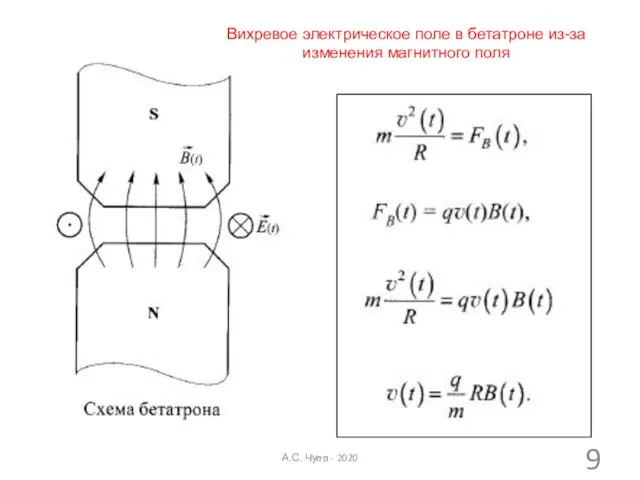
- 9. А.С. Чуев - 2020 Вихревое электрическое поле в бетатроне из-за изменения магнитного поля
- 10. Ускорение частицы Циркуляция вектора Е Сила после подстановки Е m Увеличением В (тока в катушках) производим
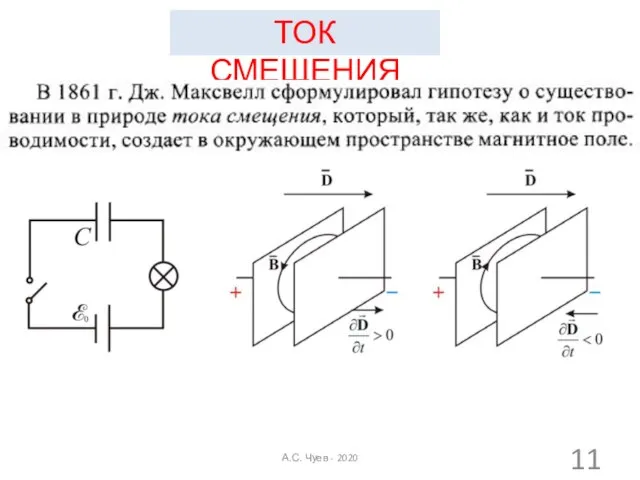
- 11. ТОК СМЕЩЕНИЯ А.С. Чуев - 2020
- 12. А.С. Чуев - 2020
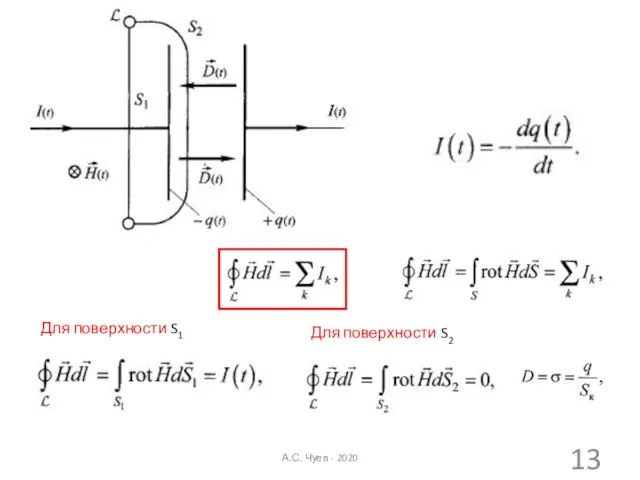
- 13. Для поверхности S1 Для поверхности S2 А.С. Чуев - 2020
- 14. Для поверхности S2 вводится ток смещения Плотность тока смещения: А.С. Чуев - 2020
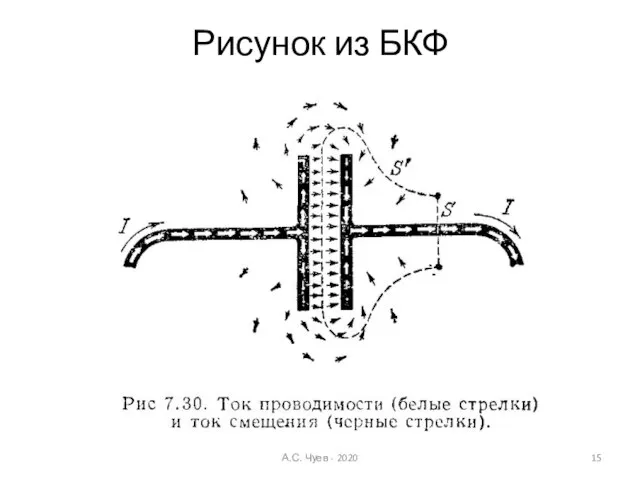
- 15. Рисунок из БКФ А.С. Чуев - 2020
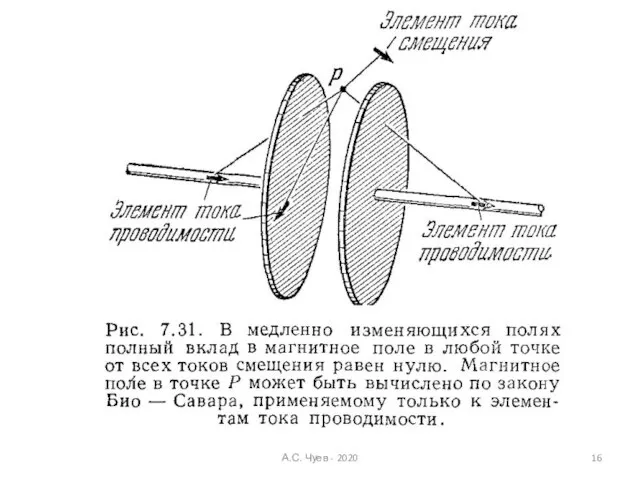
- 16. А.С. Чуев - 2020
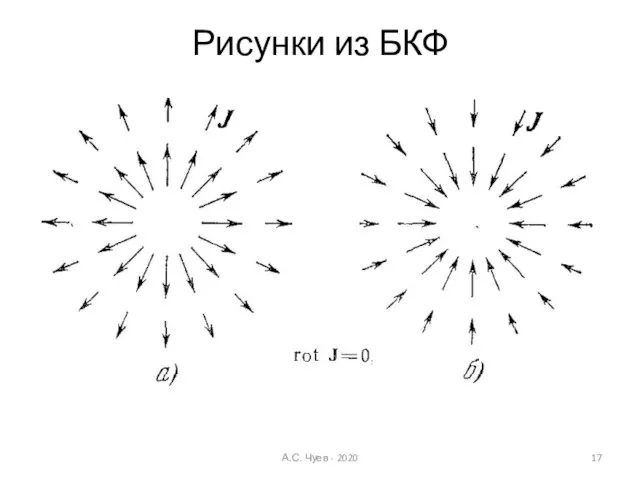
- 17. Рисунки из БКФ А.С. Чуев - 2020
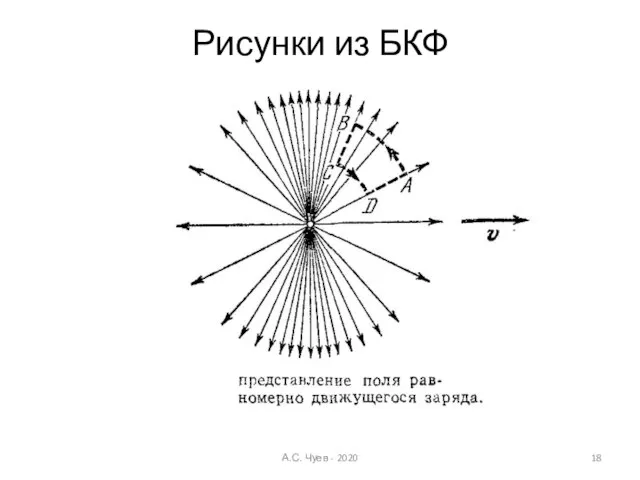
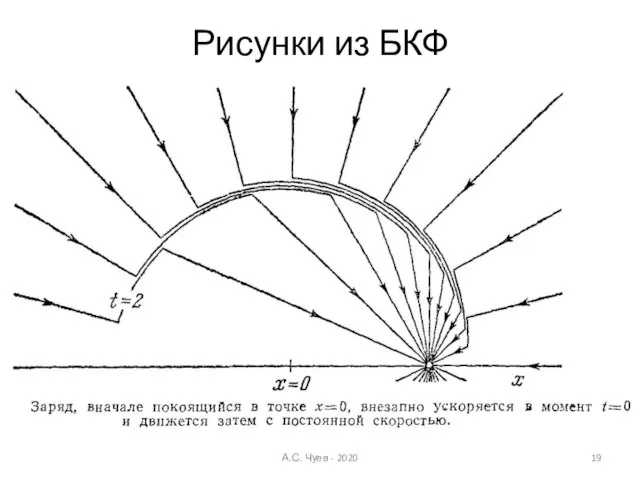
- 18. Рисунки из БКФ А.С. Чуев - 2020
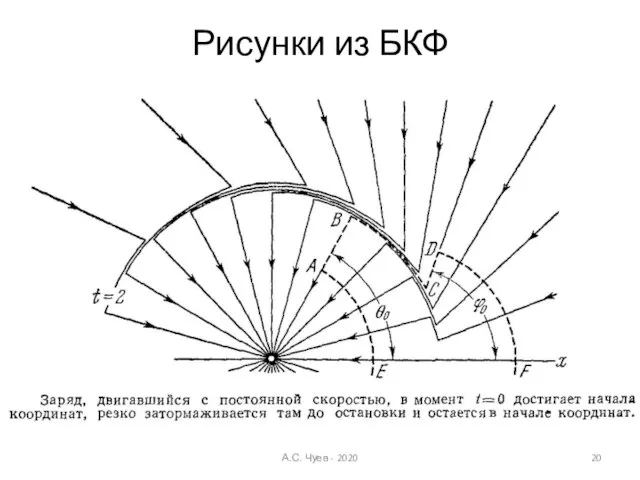
- 19. Рисунки из БКФ А.С. Чуев - 2020
- 20. Рисунки из БКФ А.С. Чуев - 2020
- 21. Уравнения Максвелла для вакуума Закон Гаусса в электричестве Закон Гаусса в магнетизме Закон Фарадея Закон Ампера
- 22. Закон полного тока А.С. Чуев - 2020
- 23. Далее: С учетом теоремы Гаусса: Выводим уравнение непрерывности: Это уравнение является следствием закона сохранения электрического заряда.
- 24. Система уравнений Максвелла в интегральной форме А.С. Чуев - 2020 4 уравнения
- 25. Система уравнений Максвелла в дифференциальной форме А.С. Чуев - 2020
- 26. Дифференциальные уравнения Максвелла в иной форме: А.С. Чуев - 2020
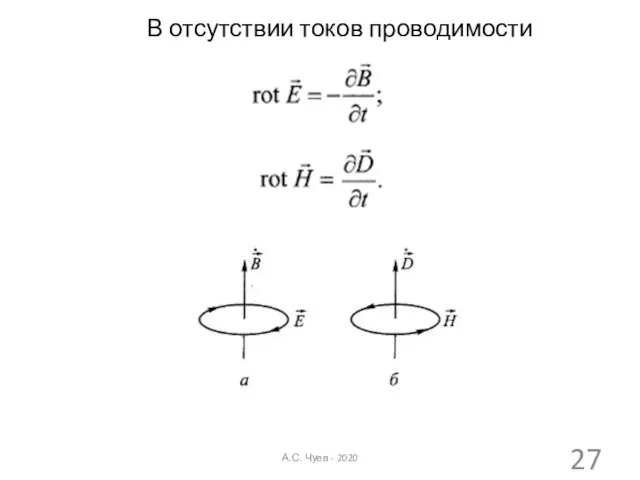
- 27. В отсутствии токов проводимости А.С. Чуев - 2020
- 28. Для замыкания уравнений Максвелла используются уравнения материальной среды А.С. Чуев - 2020 3 уравнения
- 29. Далее факультативный материал А.С. Чуев - 2020
- 30. основной А.С. Чуев - 2020
- 31. Подробности А.С. Чуев - 2020
- 32. Добавления и примечания Здесь Е внутр. А.С. Чуев - 2020
- 33. Решение уравнений Максвелла 1 – точка наблюдения; 2 – точка расположения источника поля. А.С. Чуев -
- 34. Решение уравнений Максвелла Уравнение Пуассона для вектора А: А.С. Чуев - 2020
- 35. Определения скалярного и векторного потенциалов 1 – точка наблюдения; 2 – точка расположения источника поля. А.С.
- 36. Определение векторного потенциала через магнитный момент кругового тока А.С. Чуев - 2020
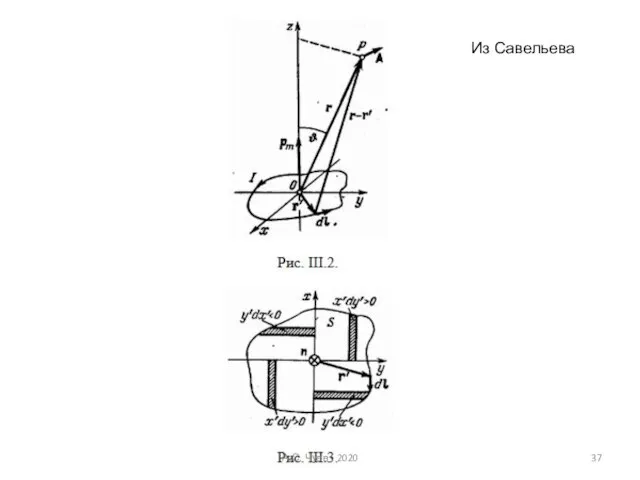
- 37. Из Савельева А.С. Чуев - 2020
- 38. Плотности зарядов и токов выступают как вторые производные скалярного и векторного потенциалов Уравнение Пуассона для скалярного
- 39. Аналогии интегральных соотношений А.С. Чуев - 2020
- 40. Аналогии дифференциальных соотношений А.С. Чуев - 2020
- 41. Из системных представлений: Уравнения Максвелла с использованием «материальных векторов» А.С. Чуев - 2020
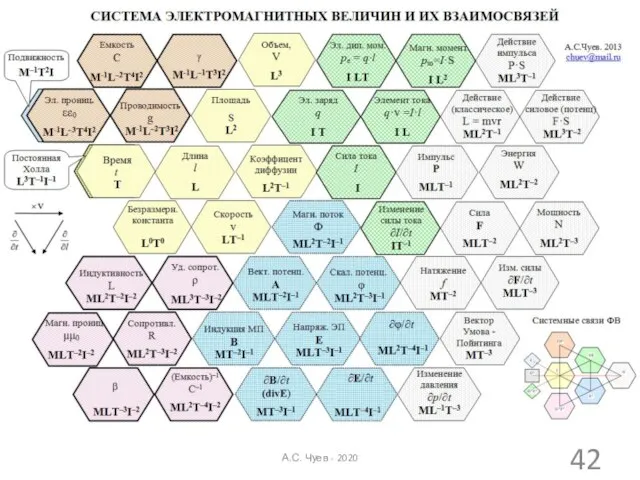
- 42. А.С. Чуев - 2020
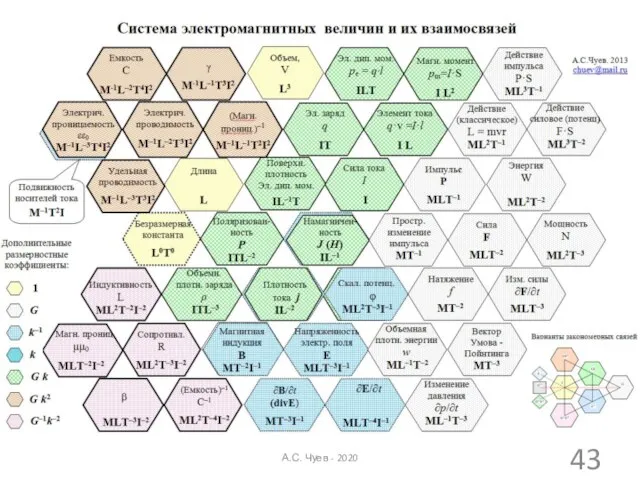
- 43. А.С. Чуев - 2020
- 45. Скачать презентацию




























 Механическая работа. Мощность
Механическая работа. Мощность Состав и строение атома
Состав и строение атома Ядерные реакции под действием нейтронов. (Тема 2.6)
Ядерные реакции под действием нейтронов. (Тема 2.6) Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо
Тема урока: Магнитное поле катушки с током. Электромагнит. Цель урока: исследовать зависимость силы магнитного поля катушки с токо Назначение основных размеров опор и определение нагрузок, действующих на опоры
Назначение основных размеров опор и определение нагрузок, действующих на опоры Фотоэффект
Фотоэффект Мир вокруг нас
Мир вокруг нас Квантовая биофизика
Квантовая биофизика Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью Презентация на тему Электробезопасность
Презентация на тему Электробезопасность  Измерение cилы трения
Измерение cилы трения Задача №16 Магнитная пушка
Задача №16 Магнитная пушка Сиракузы. III век до нашей эры
Сиракузы. III век до нашей эры Основные понятия теории механизмов и машин
Основные понятия теории механизмов и машин Диоды Ганна
Диоды Ганна Неравномерное движение. Мгновенная скорость
Неравномерное движение. Мгновенная скорость Последовательное соединение
Последовательное соединение Звук и его характеристики
Звук и его характеристики Разнообразие веществ в окружающем мире
Разнообразие веществ в окружающем мире Презентация на тему Деление ядер урана Атомная энергетика
Презентация на тему Деление ядер урана Атомная энергетика  Аналогово-цифровой контроллер
Аналогово-цифровой контроллер Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Основные законы электрической цепи постоянного тока
Основные законы электрической цепи постоянного тока Основы квантовой физики
Основы квантовой физики Автосцепное устройство
Автосцепное устройство Воздухоплавание
Воздухоплавание Презентация на тему Молекулярная физика. Ученые и их открытия
Презентация на тему Молекулярная физика. Ученые и их открытия  Диагностика дизельных двигателей
Диагностика дизельных двигателей