Понятие о цветовом пространстве на примере RGB. Цвет как вектор. Изменение яркости и насыщенности

Есть две принципиально различные системы оценки и представления цвета. Первая — колориметрическая система. В ее основе лежат основные излучения, смешивая которые, воспроизводят все многообразие цветов. Некоторые колориметрические системы имеют международную стандартизацию. Вторая—система спецификации цветов, где цвет имеет материальный носитель в виде окрашенных образцов, расположенных в определенном порядке. Системы спецификации стандартизируются национальными службами стандартизации. В последнее время системы спецификации имеют стандартное измерение цветов в международных колориметрических системах.
В основе обеих систем лежит такое фундаментальное понятие, как цветовое пространство.

Содержание
5.1. Цветовое пространство
5.2. Системы спецификации

5.1. Цветовое пространство
5.1.1. Общие представления о цветовом
пространстве
5.1.2. Определение цвета как векторной величины

5.1.1. Общие представления о цветовом
пространстве
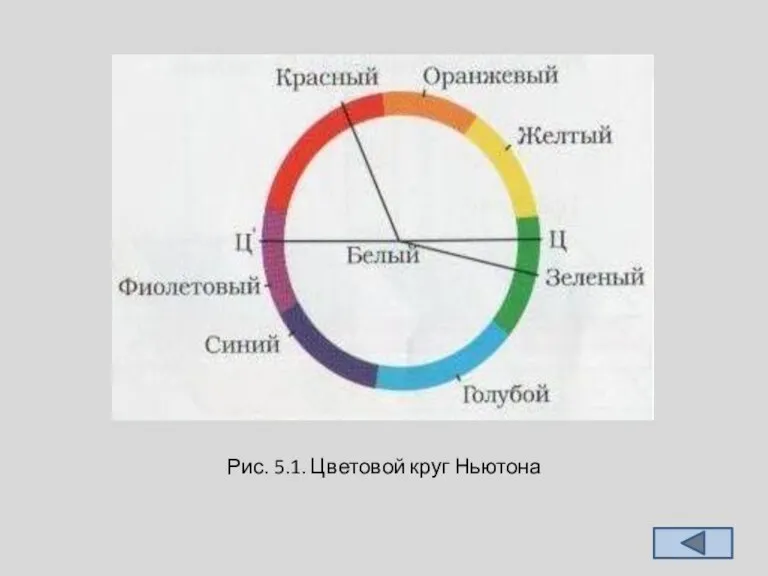
Основы научного представления о цвете были заложены Ньютоном. Он предложил систематизировать цвета при помощи белого света, разложенного призмой в спектр. Этот спектр Ньютон расположил по кругу (рис. 5.1) и указал на существование семи основных цветов спектра (КОЖЗГСФ — первые буквы названий цветов излучений).
Впоследствии между фиолетовым и красным монохроматическими излучениями были помещены бихроматические пурпурные цвета. Все природные цвета располагаются внутри круга с белой точкой в центре, цвета плавно переходят один в другой. Насыщенность увеличивается от центра круга к периферии.

Рис. 5.1. Цветовой круг Ньютона

В настоящее время устоявшимся является трехмерное представление о цветовом пространстве и его строении. Ниже рассмотрим основные принципы строения цветового пространства.
В колориметрии цвет оценивается по координатам цвета. Эти координаты получают с учетом цветовой температуры источника света, его цветовых стимулов, или, говоря иначе, в соответствии с математической моделью нашего зрения.

Цветовые пространства, используемые в современных системах спецификации и международных колориметрических системах, имеют общие признаки, лежащие в основе их построения:
1. Признается трехмерность цвета, так как цвет выражается тремя независимыми переменными (векторами основных излучений или цветовыми стимулами).
2. Цветовое тело всех реальных цветов (это часть цветового пространства) строится вокруг ахроматической оси, где черный цвет внизу, белый — вверху. Причем для самосветящихся объектов светлота (brightness) меняется от невидимой до слепящей. Для несамосветящихся объектов светлота (lightness) меняется от минимальной (черный цвет) до максимальной (белый цвет).
3. Последовательность цветов определяется спектром. Интервал между красным и фиолетовым цветами занимают пурпурные цвета. Геометрически это замкнутая фигура.

4. Чем дальше от ахроматической оси находится цвет, тем он более насыщен. Ахроматические цвета не имеют цветности и насыщенности — только светлоту.
5. Цвета одного цветового тона находятся на полуплоскостях, проходящих через ахроматическую ось (справа или слева), и называются вертикальными сечениями цветового тела.
6. Цветовой тон в вертикальном сечении цветового тела не изменяется. В вертикальном сечении изменяются цвета за счет изменения насыщенности в направлении от ахроматической оси до самых насыщенных. Цвет также изменяется за счет изменения светлоты в направлении снизу вверх параллельно ахроматической оси.

Рис. 5.2. Цветовое тело

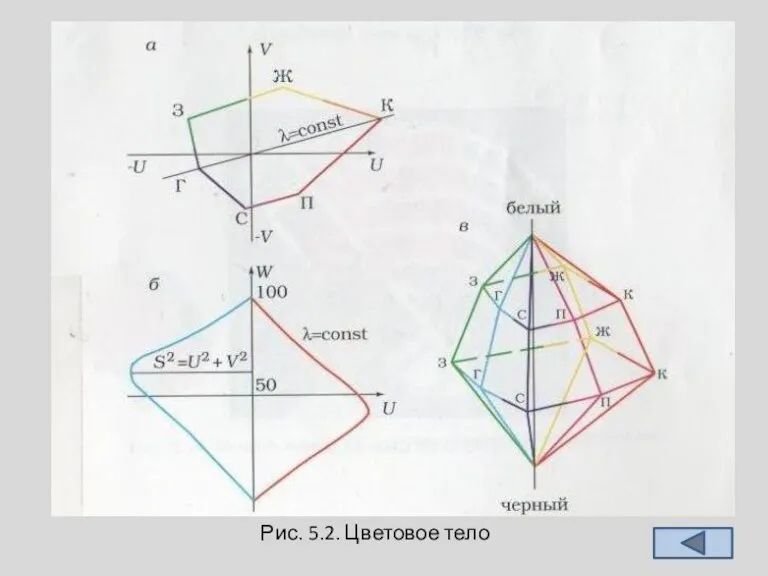
Цветовой охват показывает все многообразие цветов, принадлежащих данной плоскости (или спроецированные на нее единичные цвета), которое может быть воспроизведено данной триадой основных. Это многообразие цветов находится внутри геометрической фигуры, полученной соединением основных цветов или максимально насыщенных. Если цветовой охват построен в трехмерном пространстве, то это — цветовое тело (рис. 5.2, в).

5.1.2. Определение цвета как векторной величины
На основании законов сложения цветов (законов Грассмана), устанавливающих трехмерность цвета и непрерывность его изменения в спектре, любой цвет можно представить точкой в трехмерном пространстве. В этом пространстве каждому цвету будет соответствовать определенная точка, а каждой точке такого пространства—определенный цвет. Таким образом, цветовое пространство можно считать формой геометрического представления различных цветов. Для упорядочения цветов и выполнения над ними различных математических действий в цветовом пространстве вводят систему цветовых координат.

Таких систем в цветовом пространстве может быть великое множество. Как правило, началом координат служит точка, соответствующая черному цвету. В этой точке вообще отсутствует свет. Система цветовых координат полностью определяется заданием координатных осей и выбранным на них масштабом. В любой выбранной системе цветовых координат каждый цвет выражается через основные цвета этой системы. Главным ограничением при выборе основных является обязательная линейная независимость цветов, т.е. Чтобы ни один из основных не мог быть получен смешением двух других и сумма основных в равных количествах давала ахроматический цвет. В остальном выбор основных цветов, направление осей, масштаб на осях произвольны и зависят от поставленной цели.

При выборе осей новой системы цветов и произвольном их расположении цветовое пространство может измениться по сравнению с первоначальным. Это означает, что могут измениться положения точек, представляющих различные цвета, но соотношения между цветами при этом меняться не должны.
Цвет можно представить в цветовом пространстве не только точкой, но и цветовым вектором. Его начало будет совпадать с началом координат, а конец — с точкой данного цвета. В этом случае координаты цвета будут являться координатами цветового вектора.

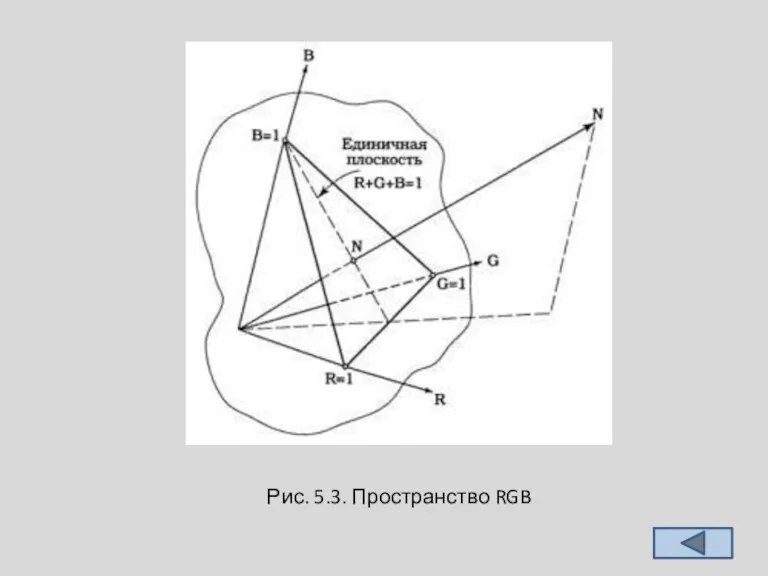
На рис. 5.3 изображено цветовое пространство неких основных цветов — красного, зеленого и синего, обозначенных RGB. Эти координаты могут быть прямоугольными или косоугольными — это несущественно. При изменении углов между координатными осями происходит расширение или сжатие цветового пространства. Существенно, что оси выходят из одной точки и не лежат в одной плоскости. Это означает, что координаты задаются тремя величинами.
На рисунке также видно, что если по осям выбрать одинаковый масштаб по основным, то плоскость, проведенная через эти основные, отсечет равносторонний треугольник, через 1/3 высоты которого пройдет вектор ахроматических цветов.

Рис. 5.3. Пространство RGB

Направление вектора указывает на увеличение светлоты. Любой другой вектор, не совпадающий с ахроматическим, будет выражать не только светлоту, но и цветность. Чем ближе к осям будет проходить вектор цвета, тем больше будут выражены насыщенность и цветовой тон.
Основные для воспроизведения координат точки белого цвета при определенной цветовой температуре выбираются практически в визуальном колориметре. На одну половину призмы проецируется белый свет, на другой половине подбирается соотношение цветов RGB, которые и будут выбраны в качестве основных.

Рассмотренный выше треугольник называют треугольником единичных цветов, так как соответствующая ему плоскость проходит через три точки с координатами 1R, 1G, 1B. Положение следа вектора, проходящего через треугольник (или продолжения вектора), имеет сумму координат, равную единице, т.е.модуль цветов, принадлежащих данной плоскости, равен единице, m = 1. Координаты единичных цветов обозначаются теми же буквами, что и координаты цветов, но строчными.
Если единичные цвета спроецировать на белый экран для сравнения рядом, то окажется, что они различаются по яркости. Очевидно, что, изменяя количества основных, можно подобрать их так, чтобы цвета были одинаковыми по яркости, но при этом не все основные будут принадлежать плоскости единичных цветов, они будут принадлежать плоскости равных яркостей.

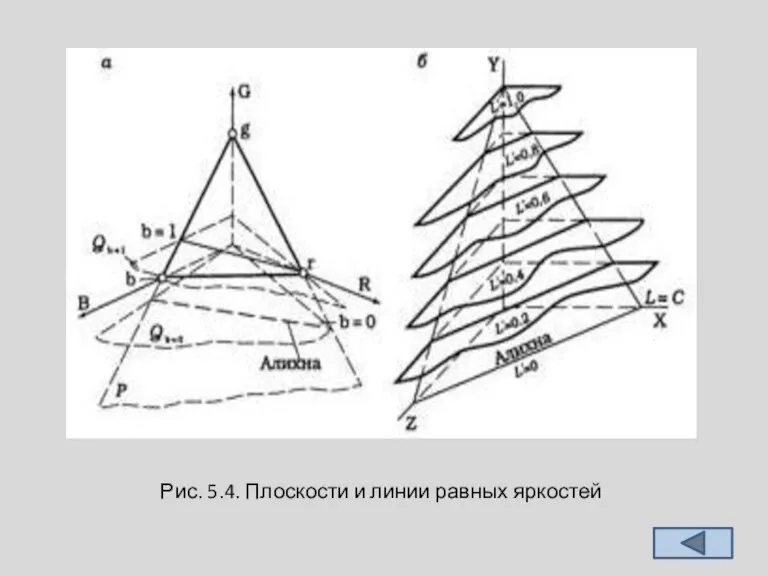
Это хорошо видно, если на осях (рис. 5.3) в том же масштабе отложить количества основных, имеющих одина-ковые яркости. Если через концы новых векторов провести плоскость равных яркостей, то эта плоскость пересечется с единичной плоскостью по прямой линии — линии равных яркостей. Из этого следует, что некоторые единичные цвета принадлежат двум плоскостям и имеют одинаковые яркости (рис. 5.4, а). Таких линий (и плоскостей) можно провести множество и все они будут параллельны (рис. 5.4, б).
В колориметрии вводится понятие плоскости нулевых яркостей, т.е. такой плоскости, где яркость отсутствует. Пересечение плоскости нулевых яркостей или алихну (греч. αλνχνα – без света). Плоскость нулевых яркостей и алихна используются для построения специфических колориметрических систем типа XYZ, которые будут рассмотрены далее.

Рис. 5.4. Плоскости и линии равных яркостей

Большинство колориметрических систем используют аддитивный синтез цвета. Поэтому принцип составления уравнений цвета и цветности тот же самый. Возникают те же проблемы с отрицательными членами уравнения цвета. А это значит , что не все реальные цвета лежат в треугольнике единичных цветов.
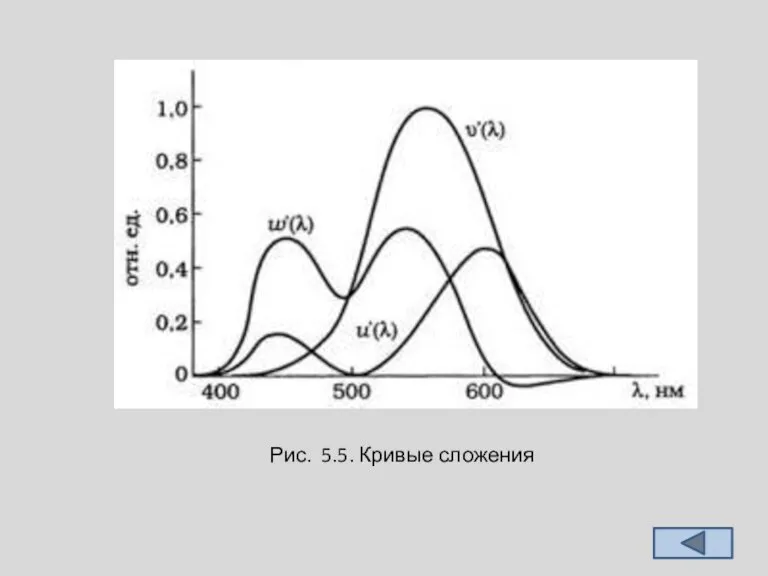
Для определения области единичных цветов, которую занимают цвета, воспринимаемые глазом (цветовой охват глаза, в данной системе координат), используют следующий прием. Находят координаты цвета монохроматических излучений, имеющих мощность 1 Вт, это так называемые кривые сложения (рис. 5.5). Другими словами, кривые сложения показывают, какое количество основных надо смешать, чтобы получить цвета, визуально не отличимые от спектральных единичной мощности.

Рис. 5.5. Кривые сложения

Поскольку в системах RGB основные реальны, то кривые сложения измеряются экспериментально, на визуальном колориметре способом, описанным выше. Отсюда следует, 650 что в функциях кривых сложения R участвуют кривые основных возбуждений глаза, или, по-другому, спектральные чувствительности глаза.
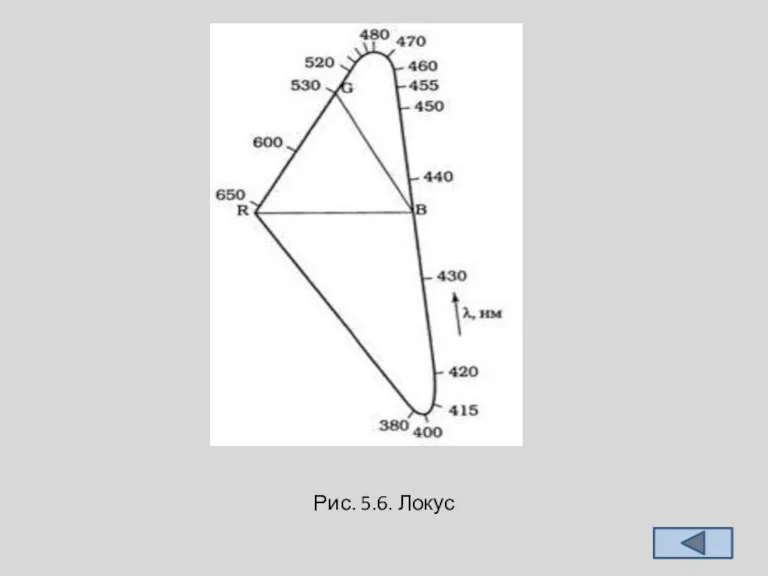
Нанеся координаты кривых сложения на единичную плоскость, получим фигуру, называемую локусом (для получения замкнутой фигуры надо соединить точки красных и фиолетовых цветов). Фактически это цветовой охват зрительного аппарата человека, изображенный в данной системе координат (рис. 5.6). Цвета, находящиеся вне локуса, нереальны. Человеческое зрение нереальные цвета не воспринимает.

Рис. 5.6. Локус

Каждая координата цвета в системах RGB несет информацию о количестве основных и об яркости (или светлоте). При изменении координат изменяются оба параметра, что вызывает определенные сложности. Другими словами, изменение количества основных приводит к изменению не только цветности, но и яркости. Количество изменяемых параметров больше двух, что затрудняет процесс регулирования при аддитивном синтезе.

Систем координат может быть бесконечное множество. Из математики известно, что для перехода из одной системы координат в другую необходимо основные одной системы выразить через основные другой системы, т.е. получить матрицу пересчета или соответствующую формулу:
X = XrR + XgG + XbB,
Y = YrR + YgG + YbB, (5.1.1)
Z = ZrR + ZgG + ZbB,
где Xr, Yr, Zr – координаты R, выраженные в системе XYZ; Xg, Yg, Zg – координаты G, выраженные в системе XYZ;
Xb, Yb, Zb – координаты B, выраженные в системе XYZ.

Если формулы соответствует линейным преобразованиям, то это так называемые «проективные преобразования». Раз известны кривые сложения в одной из систем координат, их можно рассчитать в любой другой, если матрица есть матрица пересчета.
Исследователи, пытавшиеся уйти от отрицательных координат и упростить расчет яркости, предложили перейти от реальных основных типа RGB к нереальным, которые обозначили, например, XYZ. Это математические символы, которыми обозначают неизвестные.

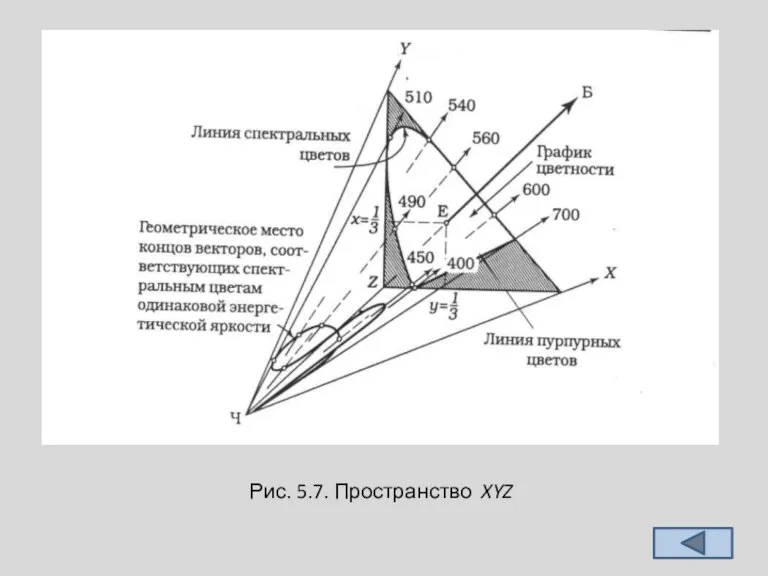
В результате расчетов выяснилось, что для получения только положительных координат цвета необходимо использовать основные повышенной насыщенности, насыщенности большей, чем у спектральных цветов. В этом случае все спектральные цвета будут находиться в треугольнике единичных цветов. А если выбрать основные так, чтобы X и Z принадлежали плоскости нулевых яркостей, то за яркость будет отвечать только координата Y. На рис. 5.7 приведена одна из систем типа XYZ.

Рис. 5.7. Пространство XYZ

Еще одна новация в системе XYZ. Для приближения к цветовой модели зрения используются различные источники света, что как бы моделирует цветовую адаптацию глаза. При этом белая точка перемещается по плоскости единичных цветов. Соответственно меняются количества основных, необходимых для получения вектора ахроматических цветов.
Из множества предложенных систем типа XYZ была принята система, предложенная Гилдом и Райтом.
Другая система была предложена в 1960 г. Эта же система была модернизирована в 1964 г. и окончательно принята в 1976 г. под названием CIELUV. Следует отметить, что в этой системе преобразования проективные только для единичных цветов яркости изменяются по кубическому закону.

Кроме векторного цветового пространства в колориметрии используют пространство цветовых ощущений, приближающееся к модели восприятия цвета человеком. Переход от пространства типа CIEXYZ к пространству CIELAB нелинеен, поэтому пространства CIELAB и частично CIELUV не векторные. Такие модели используют в основном в системах спецификации, но начиная с 1976 г. после появления системы CIELAB (для аддитивного синтеза CIELUV) эти модели используются для расчета цветовых различий и моделирования цветового пространства в полиграфии.