Содержание
- 2. ПРОСТЫЕ МЕХАНИЗМЫ. С незапамятных времен человек использует для совершения механической работы различные приспособления. Каждому известно, что
- 3. Во многих случаях вместо того чтобы поднимать тяжелый груз на некоторую высоту, его вкатывают или втаскивают
- 4. К простым механизмам относятся: рычаг и его разновидности – блок, ворот; наклонная плоскость и ее разновидности
- 5. Рычаг. Равновесие сил на рычаге. Рассмотрим самый простой и распространенный механизм – рычаг. Рычаг представляет собой
- 6. Рабочему нужно преодолеть вес груза P – силу, направленную вертикально вниз. Он поворачивает для этого лом
- 7. КРАТЧАЙШЕЕ РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ ОПОРЫ И ПРЯМОЙ, ВДОЛЬ КОТОРОЙ ДЕЙСТВУЕТ НА РЫЧАГ СИЛА, НАЗЫВАЕТСЯ ПЛЕЧОМ СИЛЫ
- 9. Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого
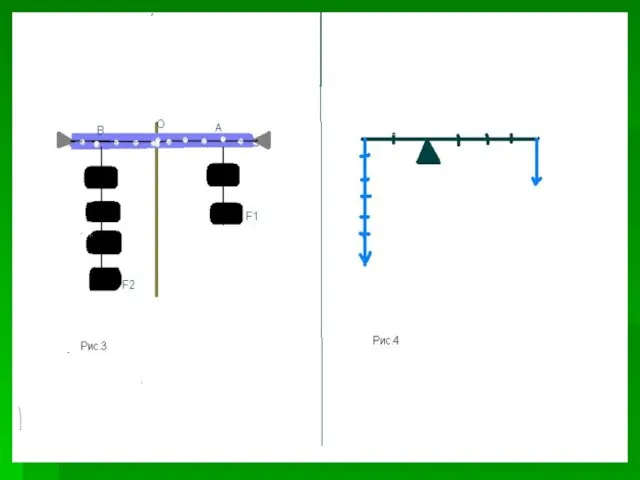
- 10. К рычагу (рис3) по обе стороны от точки опоры подвешивают различные грузы так, чтобы рычаг каждый
- 11. ПРАВИЛО РАВНОВЕСИЯ. На основании таких опытов было установлено условие(правило) равновесия рычага. РЫЧАГ НАХОДИТСЯ В РАВНОВЕСИИ ТОГДА,
- 12. ФОРМУЛА Это правило можно записать в виде формулы : F1:F2 = L1:L2 , где F1 и
- 13. Правило равновесия рычага было установлено Архимедом около 287-212 гг. до н.э. Из этого правила следует, что
- 14. МОМЕНТ СИЛЫ. Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы ; он обозначается
- 15. РЫЧАГ НАХОДИТСЯ В РАВНОВЕСИИ ПОД ДЕЙСТВИЕМ ДВУХ СИЛ, ЕСЛИ МОМЕНТ СИЛЫ, ВРАЩАЮЩЕЙ ЕГО ПО ЧАСОВОЙ СТРЕЛКЕ,
- 16. Это правило, называемое правилом моментов, можно записать в виде формулы : М1 = М2 Действительно, в
- 17. Момент силы характеризует действие силы и показывает, что оно зависит одновременно и от модуля силы, и
- 19. Скачать презентацию















 Введение. Кинематика поступательного и вращательного движения вопросы
Введение. Кинематика поступательного и вращательного движения вопросы Lektsia_StRT_2 (1)
Lektsia_StRT_2 (1) Двигатель Внутреннего Сгорания
Двигатель Внутреннего Сгорания Типы астрономических объектов: галактики, звезды, планеты, астероиды, кометы, диффузное вещество
Типы астрономических объектов: галактики, звезды, планеты, астероиды, кометы, диффузное вещество Разработка модели и исследование процессов в электроприводе постоянного тока
Разработка модели и исследование процессов в электроприводе постоянного тока Термодинамика и теплопередача. Реальные газы
Термодинамика и теплопередача. Реальные газы Ультрофеолетовые волны
Ультрофеолетовые волны Система охлаждения двигателя
Система охлаждения двигателя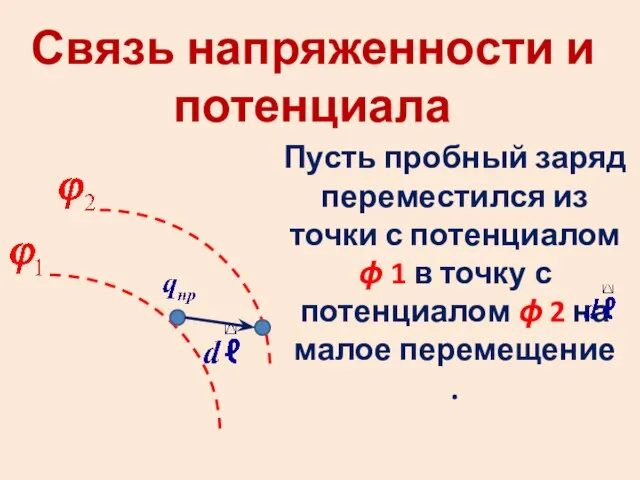 Связь напряженности и потенциала
Связь напряженности и потенциала Электроосветительные приборы. Лампы накаливания и регулировка освещенности
Электроосветительные приборы. Лампы накаливания и регулировка освещенности Презентация по физике "Что? Где? Когда?" -
Презентация по физике "Что? Где? Когда?" -  Физический маятник
Физический маятник Давление жидкостей и газов. 7 класс
Давление жидкостей и газов. 7 класс Единицы работы электрического тока, применяемые на практике
Единицы работы электрического тока, применяемые на практике Цепи синусоидального тока. Лекция 6
Цепи синусоидального тока. Лекция 6 Чувствительность взрывчатых систем к внешним воздействиям
Чувствительность взрывчатых систем к внешним воздействиям Презентация на тему Квантовая физика
Презентация на тему Квантовая физика  Презентация на тему Тепловые машины и их КПД
Презентация на тему Тепловые машины и их КПД  Сопротивление и пассивные фильтры
Сопротивление и пассивные фильтры Презентация на тему Цепные ядерные реакции
Презентация на тему Цепные ядерные реакции  Основы МРТ
Основы МРТ Электризация тел. Электрический заряд. Закон сохранения электрического заряда
Электризация тел. Электрический заряд. Закон сохранения электрического заряда Дома:§62,63 Цель урока: Познакомиться с понятием энергии, как способностью тела совершать работу. Рассмотреть примеры тел, обладающих энергией. Познакомиться с видами энергии.
Дома:§62,63 Цель урока: Познакомиться с понятием энергии, как способностью тела совершать работу. Рассмотреть примеры тел, обладающих энергией. Познакомиться с видами энергии. Технологический расчет комплекса технического обслуживания с разработкой проекта зоны
Технологический расчет комплекса технического обслуживания с разработкой проекта зоны Закон сохранения импульса
Закон сохранения импульса Основные понятия электродинамики
Основные понятия электродинамики Элективный курс Экспериментальная физика
Элективный курс Экспериментальная физика Линзы. Построение изображений в линзах
Линзы. Построение изображений в линзах