Слайд 2 1. Момент силы.
Момент силы относительно оси - величина, характеризующая вращательное действие

силы и равная векторному произведению радиуса-вектора точки приложения силы на составляющую вектора силы в плоскости перпендикулярной оси вращения.
Плечо силы (h)- кратчайшее расстояние от оси вращения до линии действия силы:
Направление вектора момента силы определяется правилом буравчика.Модуль вектора момента силы равен произведению перпендикулярной оси составляющей вектора силы на её плечо.
Момент силы равен нулю, если линия действия силы:
1)параллельна оси 2)вращения пересекает ось вращения
Слайд 4 Момент инерции.
Момент инерции тела- мера его инертности во вращательном движении, равен

сумме моментов инерции всех материальных точек, составляющих данное тело. Момент инерции зависит от распределения массы тела относительно оси вращения, т.е. зависит от положения оси вращения.
Примеры: 1)Момент инерции полого тонкостенного цилиндра радиусом R относительно его оси
2) Момент инерции сплошного однородного цилиндра (диска) относительно его оси. Сплошной цилиндрический диск высотой h , радиусом R , массой m, плотностью ρ. Элемент массы- тонкостенный цилиндр радиусом r , толщиной стенки dr , массой dm.
Слайд 5Момент инерции твердого тела относительно произвольной оси. Теорема Штейнера
Момент инерции тела относительно

произвольной оси равен сумме момента инерции тела относительно параллельной оси, проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями .
Слайд 6Момент Импульса материальной точки.
Момент импульса материальной точки относительно оси- векторная характеристика вращательного

движения, равная векторному произведению её радиуса- вектора на вектор импульса.
Момент импульса абсолютно твёрдого тела (системы материальных точек ) равен сумме моментов импульса всех составляющих его материальных точек:
Момент импульса АТТ относительно некоторой оси равен произведению его момента инерции относительно данной оси на вектор угловой скорости.
Слайд 7Основной закон динамики вращательного движения абсолютно твёрдого тела
Угловое ускорение, приобретаемое телом, при

вращении вокруг неподвижной оси прямо пропорционально результирующему моменту действующих на тело сил и обратно пропорционально моменту инерции тела относительно данной оси.
Скорость изменения момента импульса тела равна суммарному моменту всех действующих на него сил.
Слайд 8 Закон сохранения момента импульса
Экспериментально, XVIII в., Эйлер.
В ХХ в. теоретически обоснована

связь закона сохранения момента импульса с изотропностью пространства Нашей Вселенной.
ДЛЯ ЗАМКНУТОЙ СИСТЕМЫ:
Векторная сумма моментов импульсов замкнутой системы тел есть величина постоянная.
Слайд 9Кинетическая энергия вращения
В общем случае любое сложное движение АТТ можно представить как

сумму двух движений: поступательного со скоростью, равной скорости центра инерции тела Vc , и вращательного с угловой скоростью ω вокруг мгновенной оси, проходящей через центр инерции.
Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех составляющих его материальных точек.
Слайд 10 Элементарная работа i-той силы при вращении тела:
Элементарная работа равнодействующей при

вращении тела:
Работа равнодействующей всех сил при вращении тела:
Слайд 11Условия равновесия тел.
Безразличное: При любых малых отклонениях от положения равновесия равновесие не

нарушается .
Неустойчивое: При любых малых отклонениях от положения равновесия возникают силы, смещающие тело от начального положения.
Устойчивое: При любых малых отклонениях от положения равновесия возникают силы, которые стремиться возвратить тело в начальное положение.
Слайд 12Условия равновесия тела имеющего неподвижную ось вращения:
безразличное равновесие - ось вращения проходит

через центр масс
устойчивое равновесие - центр масс находится ниже оси вращения
неустойчивое равновесие –центр масс расположен выше оси вращения
Слайд 13Условия равновесия твёрдого тела
Твердое тело находится в равновесии, если равны нулю равнодействующая

приложенных к телу сил и векторная сумма моментов всех сил относительно произвольной оси.












 Ультразвуковой контроль (УЗК). Методы и оборудование УЗД
Ультразвуковой контроль (УЗК). Методы и оборудование УЗД Три состояния вещества
Три состояния вещества Горение свечи. Лабораторная работа
Горение свечи. Лабораторная работа Резонанс
Резонанс Ефективність грохочення
Ефективність грохочення Физика вокруг нас
Физика вокруг нас Кинематика. Основные понятия
Кинематика. Основные понятия Задачи по физике
Задачи по физике Метод рефрактометрии и ИК-спектроскопии
Метод рефрактометрии и ИК-спектроскопии Измерение силы тока и напряжения
Измерение силы тока и напряжения Первые полупроводниковые компоненты
Первые полупроводниковые компоненты Энергия топлива. Удельная теплота сгорания топлива
Энергия топлива. Удельная теплота сгорания топлива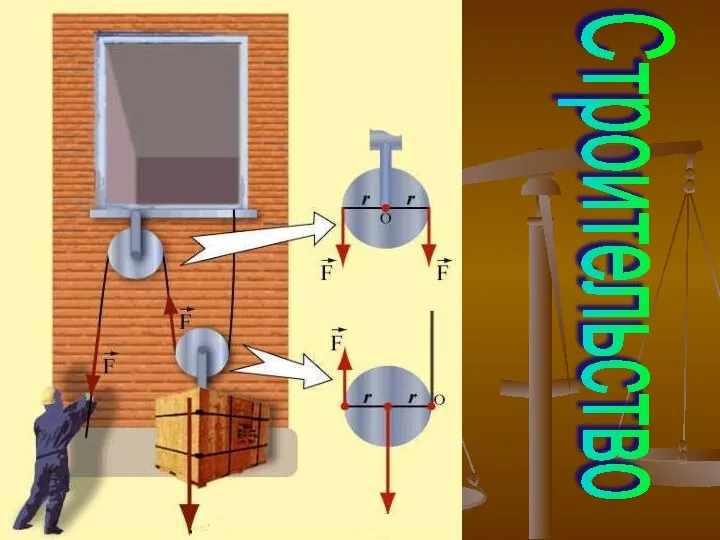 Наклонная плоскость
Наклонная плоскость Гидравлический домкрат в быту
Гидравлический домкрат в быту Строение атома
Строение атома Моя будущая профессия - инженер технической диагностики
Моя будущая профессия - инженер технической диагностики Теплофизика процесса резания
Теплофизика процесса резания Шпоночные соединёния
Шпоночные соединёния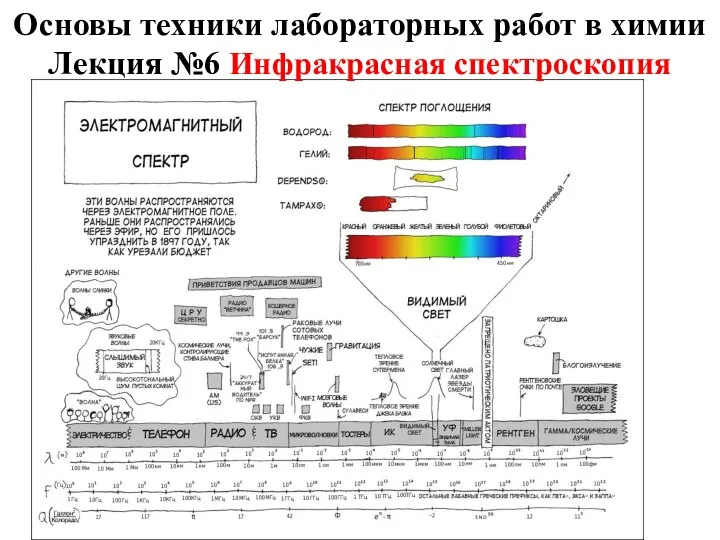 Основы постановки научного эксперимента. Инфракрасная спектроскопия. (Лекция 6)
Основы постановки научного эксперимента. Инфракрасная спектроскопия. (Лекция 6) Испарения и конденсация
Испарения и конденсация Определение температуры. Абсолютная температура
Определение температуры. Абсолютная температура Электротехника и электроника. Трёхфазные электрические цепи синусоидального тока
Электротехника и электроника. Трёхфазные электрические цепи синусоидального тока Влажность воздуха. Способы определения влажности воздуха
Влажность воздуха. Способы определения влажности воздуха Решение задач
Решение задач Колебания. Общие понятия
Колебания. Общие понятия Судовые двигатели внутреннего сгорания. Лекция 11
Судовые двигатели внутреннего сгорания. Лекция 11 Лазер - история
Лазер - история Частицы вещества
Частицы вещества