Прикладная механика. Тема 1: Кинематика точки

Литература:
Ильин В.Н., Полянин В.Д. Прикладная механика. Часть I. Механика недеформируемого твердого тела. Учебное пособие. - М.: Академия ГПС МЧС России, 2008, - 90 с.
2. Тарг С.М. Краткий курс теоретической механики. – 14-е изд., стер. – М.: Высш.шк., 2004. – 416 с.

Выбор исходных данных.
Вариант задания определяется совокупностью трех цифр, условно обозначаемой буквами АБВ.
Слушатель заочного факультета шифр АБВ выбирает из таблицы «Выбор варианта задания …» по трем последним цифрам номера своей зачетной книжки – НЗК.
Группа 5116Т – 1к5лет:
Бабин Евгений Александрович
Бакриев Якуб Михайлович
Белов Сергей Игоревич
Изюмцев Андрей Васильевич
Ильченко Дмитрий Иванович
Карнов Вячеслав Вячеславович
Касаткин Илья Игоревич
Киндяков Евгений Петрович
Коршунов Илья Александрович
Ливенцев Дмитрий Евгеньевич
Муцуев Абдулла Магомедович
НЗК = 125 АБВ = 081
НЗК = 126 АБВ = 548
НЗК = 127 АБВ = 112
НЗК = 128 АБВ = 686
НЗК = 129 АБВ = 649
НЗК = 130 АБВ = 470
НЗК = 131 АБВ = 637
НЗК = 132 АБВ = 845
НЗК = 133 АБВ = 759
НЗК = 134 АБВ = 479
НЗК = 135 АБВ = 507

Выбор исходных данных.
Вариант задания определяется совокупностью трех цифр, условно обозначаемой буквами АБВ.
Слушатель заочного факультета шифр АБВ выбирает из таблицы «Выбор варианта задания …» по трем последним цифрам номера своей зачетной книжки – НЗК.
Группа 5116Т – 1к5лет:
12. Оздоев Руслан Магомедович
13. Решетников Виктор Васильевич
14. Сафиуллов Игорь Рифтатович
15. Семенов Владислав Сергеевич
16. Сидиропуло Дионис Вячеславович
17. Степанов Артем Александрович
18. Трушин Роман Александрович
19. Чесна Сергей Альфонсавич
20. Шкомов Дмитрий Александрович
НЗК = 136 АБВ = 006
НЗК = 137 АБВ = 364
НЗК = 138 АБВ = 540
НЗК = 139 АБВ = 984
НЗК = 140 АБВ = 615
НЗК = 141 АБВ = 673
НЗК = 142 АБВ = 855
НЗК = 143 АБВ = 992
НЗК = 144 АБВ = 452

Пример оформления титульного листа контрольных работ

Разбор задания №1 «Кинематика точки»:
Выбор исходных данных.
Определение уравнения траектории и построение её на чертеже.
Для заданного момента времени t, определение:
3.1. Положения точки на траектории.
3.2. Вектора полной скорости.
3.3.Векторов касательного, нормального и полного ускорений.
3.4. Радиуса кривизны траектории.
4. Выводы.

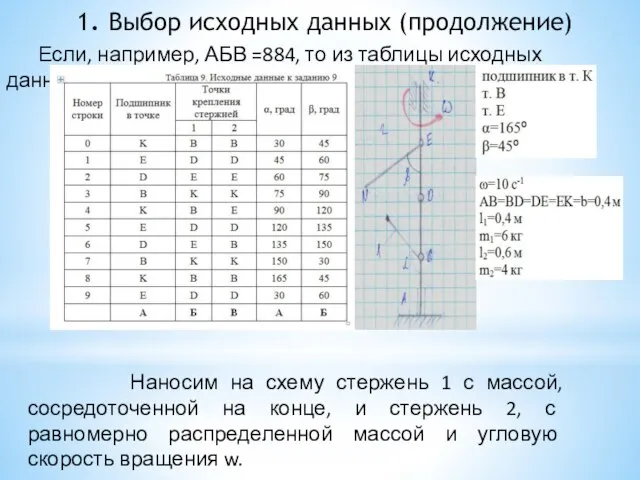
1. Выбор исходных данных (продолжение)
Если, например, АБВ = 301, то из таблицы исходных данных:
x = 2-t (см)
y = 2t2+2 (см)
t1=1,45 (c) для упрощения расчетов принимаем t1=1 (c)

2. Определение уравнения траектории и построение её на чертеже.
Уравнение траектории получаем, исключением t из уравнений движения:
x = 2-t (см) t = 2-x
y = 2t2+2 (см) y = 2(2-x)2+2 = 2x2-8x+10
Замечание: если уравнения движения содержат sin или cos, то для нахождения уравнения траектории необходимо использовать формулы: sin2α + cos2α =1
cos2α = 1 - 2 sin2α
cos2α = 2cos2α – 1
sin2 α = 2sinα cosα .

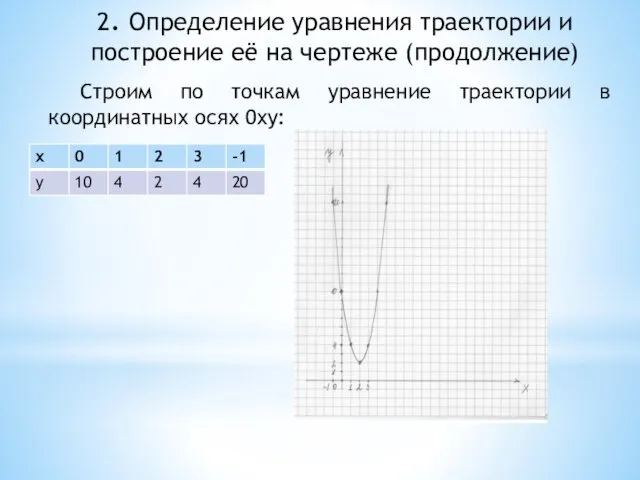
2. Определение уравнения траектории и построение её на чертеже (продолжение)
Строим по точкам уравнение траектории в координатных осях 0xy:

.
3.1. Определение положения точки на траектории.
Подставляем значение момента времени t1=1 с(в общем случае берется из исходных данных, например, для АБВ = 301 t1=1,45 с) в уравнения движения:
x (1) = 2 – t = 2 – 1 =1 (см)
y (1) = 2t2+2 = 2*12+2 = 4 (см)
Точка лежит на траектории, значит уравнение траектории найдено верно!

3.2. Определение полного вектора скорости.
Проекция вектора полной скорости на ось х – VX :
= (2-t)' = -1 (см/c)
Проекция вектора полной скорости на ось y – Vy :
= (2t2+2)' = 4t = 4 (см/c)
Значение полного вектора скорости - V:
(см/c)

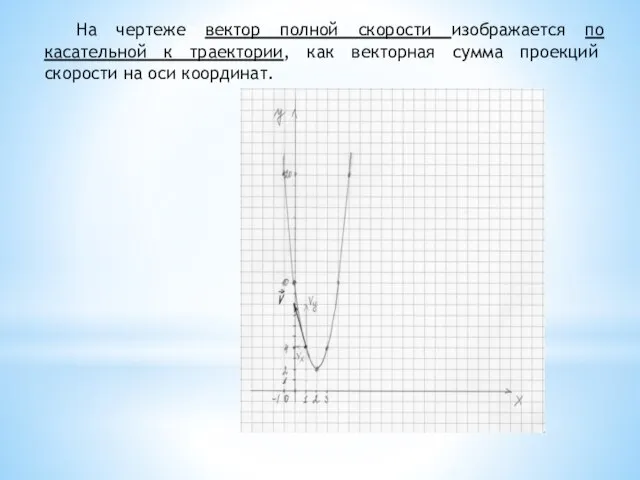
На чертеже вектор полной скорости изображается по касательной к траектории, как векторная сумма проекций скорости на оси координат.

3.3. Определение векторов касательного, нормального и полного ускорений.
Проекция вектора полного ускорения на ось х – aX :
(см/c2)
Проекция вектора полного ускорения на ось y – ay :
(см/c2)
Значение полного вектора ускорения - a:
(см/c2)
Замечание: т.к. проекция ускорения на ось x – 0, то положение вектора полного ускорения совпадает с проекцией на ось y, т.е. вектор расположен строго вертикально.

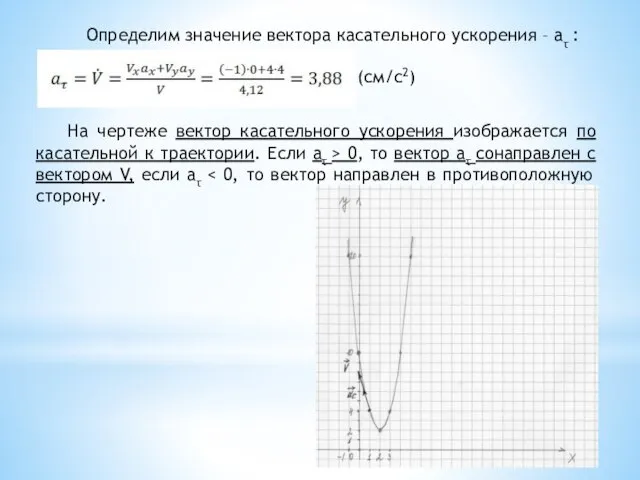
Определим значение вектора касательного ускорения – aτ :
(см/c2)
На чертеже вектор касательного ускорения изображается по касательной к траектории. Если aτ > 0, то вектор aτ сонаправлен с вектором V, если aτ < 0, то вектор направлен в противоположную сторону.

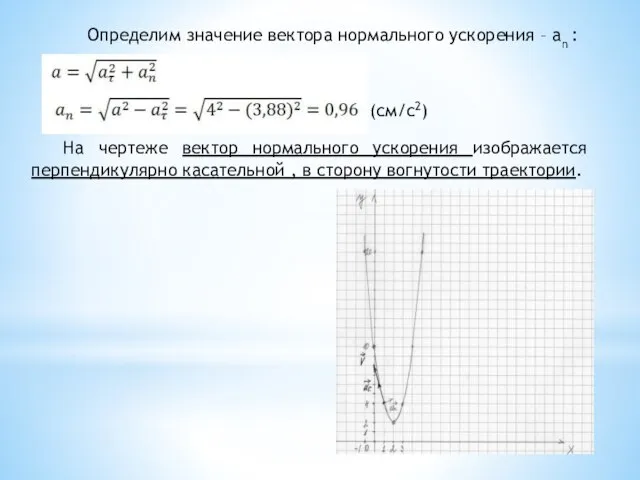
Определим значение вектора нормального ускорения – an :
(см/c2)
На чертеже вектор нормального ускорения изображается перпендикулярно касательной , в сторону вогнутости траектории.

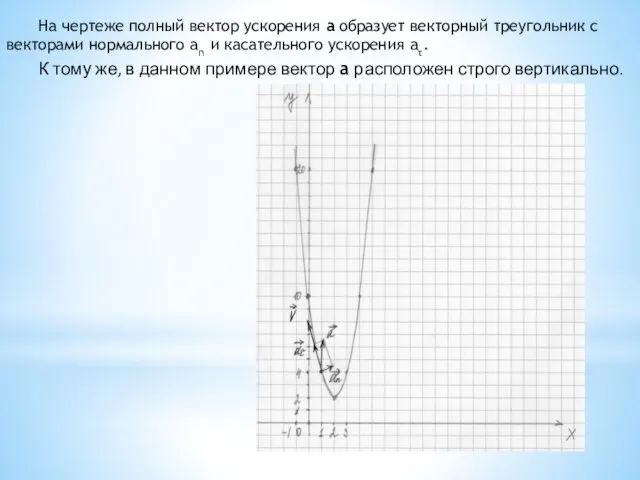
На чертеже полный вектор ускорения a образует векторный треугольник с векторами нормального an и касательного ускорения aτ.
К тому же, в данном примере вектор a расположен строго вертикально.

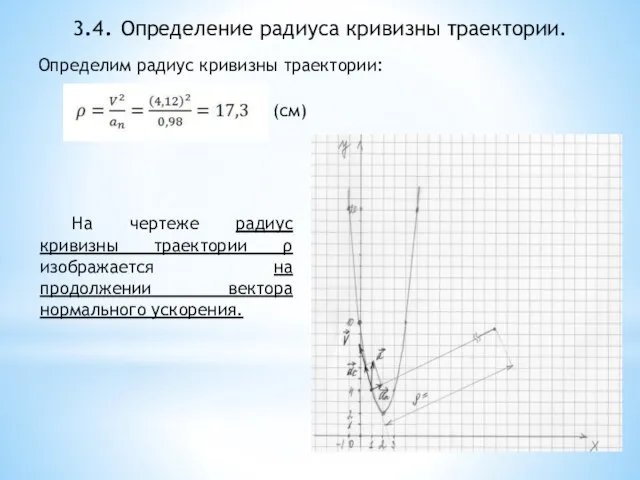
3.4. Определение радиуса кривизны траектории.
Определим радиус кривизны траектории:
(см)
На чертеже радиус кривизны траектории ρ изображается на продолжении вектора нормального ускорения.

Выводы:
1) Кинематикой называют раздел механики, в котором рассматривают движение тел и точек без учета сил, приложенных к ним.
2) Для нахождения уравнения траектории из уравнений движений следует исключить t.
3) Вектор полной скорости на чертеже изображается по касательной к траектории.
4) На чертеже вектор касательного ускорения изображается по касательной к траектории. Если aτ > 0, то вектор aτ сонаправлен с вектором V – движение ускоренное, если aτ < 0, то вектор направлен в противоположную сторону – движение замедленное.
5) На чертеже вектор нормального ускорения изображается перпендикулярно касательной , в сторону вогнутости траектории.
6) На чертеже радиус кривизны траектории ρ изображается на продолжении вектора нормального ускорения.

Разбор задания №2 «Кинематика твердого тела»:
1.Выбор исходных данных.
2.Определение скорости и ускорения звена по заданному закону движения.
3.Для заданного момента времени t, определение и построение на чертеже:
3.1. Угловых скоростей и угловых ускорений колес 1,2,3.
3.2. Скоростей и ускорений точек А,B и С.
3.3.Скоростей и ускорений рейки 4 и груза 5.
4. Выводы.

1. Выбор исходных данных (продолжение)
Если, например, АБВ =738, то из таблицы исходных данных:

2. Определение скорости и ускорения звена по заданному закону движения.
Вариант 1: в Дано φ = f(t), рад − закон вращения колеса 1,2 или 3 («+» против часовой стрелки).
Определим скорость звена: Определим ускорение звена:
Вариант 2: в Дано S = f(t), см − закон поступательного движения рейки или груза («+» сверху вниз).

3.1. Определение угловых скоростей и угловых ускорений колес 1,2 и 3.
Определив кинематические характеристики заданного звена, смотрим с каким колесом данное звено связано (точка касания или ременная передача). В точках, в которых звенья связаны, линейные скорости точек будут равны.
Замечание: линейные скорости точек на колесе связаны с угловой скоростью колеса формулой:

.
3.1. Определение угловых скоростей и угловых ускорений колес 1,2 и 3.
Большой радиус колеса 2 касается большого радиуса колеса 3:
Малый радиус колеса 3 касается малого радиуса колеса 1:

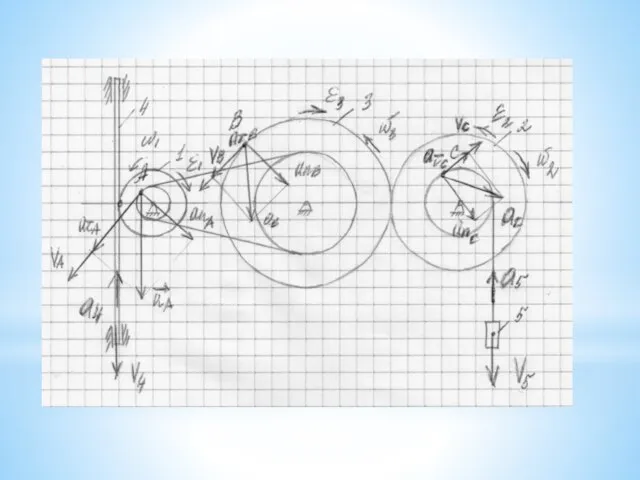
3.1. Определение угловых скоростей и угловых ускорений колес 1,2 и 3.
На чертеже направления скоростей и ускорений начинаем отмечать с заданного звена.
Затем отмечаем скорости связанных звеньев, в зависимости от типа связи (точка касания – направление скорости в противоположную сторону для колеса, в ту же сторону для рейки и груза; ременная передача - направление скорости в ту же сторону).
Направления ускорений в зависимости от знака: «+» сонаправлено со скоростью, «-» направлено в противоположную сторону.

3.2. Определение скоростей и ускорений точек A,B и C.
Точка А лежит на малом радиусе 1 колеса:

3.2. Определение скоростей и ускорений точек A,B и C.
Точка B лежит на большом радиусе 3 колеса:

3.2. Определение скоростей и ускорений точек A,B и C.
Точка С лежит на малом радиусе 2 колеса:

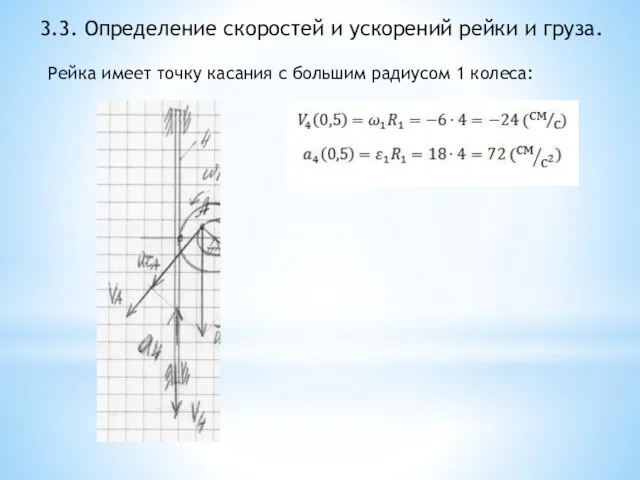
3.3. Определение скоростей и ускорений рейки и груза.
Рейка имеет точку касания с большим радиусом 1 колеса:

3.3. Определение скоростей и ускорений рейки и груза.
Груз имеет точку касания с малым радиусом 2 колеса:

4. Выводы:
1) В точках, в которых звенья связаны, - точка касания или ременная передача - линейные скорости точек будут равны, угловые скорости колес НЕ равны.
2) Линейные скорости точек на колесе связаны с угловой скоростью колеса формулой: V = ωR
3) Вектор полной скорости на чертеже изображается по касательной к траектории.
4) На чертеже вектор касательного ускорения изображается по касательной к траектории. Если aτ > 0, то вектор aτ сонаправлен с вектором V – движение ускоренное, если aτ < 0, то вектор направлен в противоположную сторону – движение замедленное.
5) На чертеже вектор нормального ускорения изображается перпендикулярно касательной , в сторону вогнутости траектории.

Разбор задания №3 «Кинематика твердого тела»:
1.Выбор исходных данных.
2. Перестроение схемы. 3.Определение скоростей всех точек механизма, обозначенных буквами на схеме и угловых скоростей всех стержней.
5. Выводы.

1. Выбор исходных данных (продолжение)
Если, например, АБВ =163, то из таблицы исходных данных:

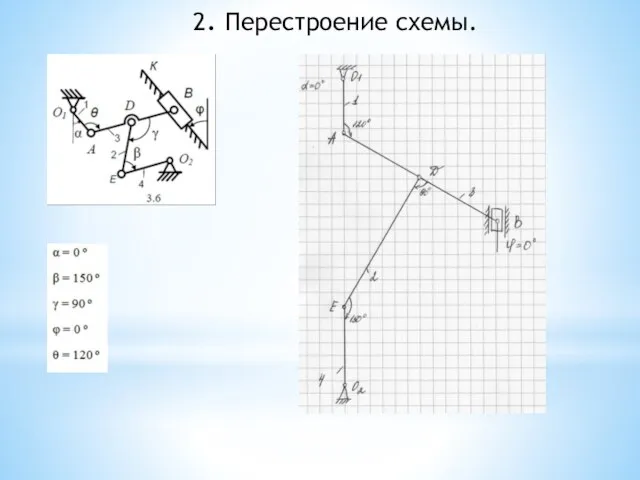
2. Перестроение схемы.

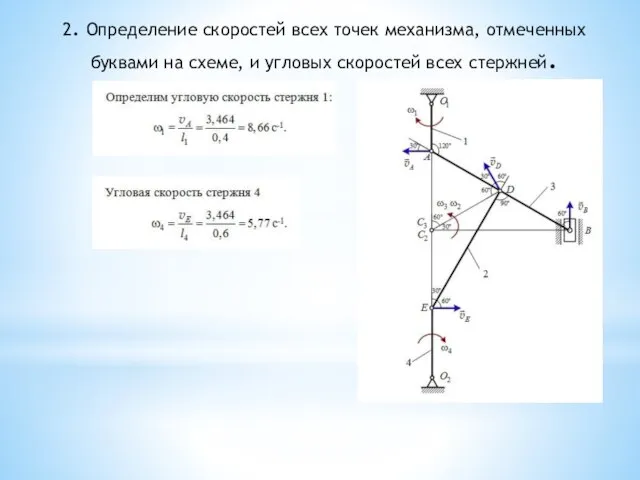
2. Определение скоростей всех точек механизма, отмеченных буквами на схеме, и угловых скоростей всех стержней.
Вариант 1: в Дано задана VB, м/c − скорость точки B (на рисунке вектор направлен от точки В к точке К ).
Анализируем, какому стержню принадлежит точка В (стержень 3).
Определяем направление скорости второго конца данного стержня (скорость VA перпендикулярна стержню 1, т.к. точка А движется по дуге окружности вокруг точки О1 – УГЛОВАЯ СКОРОСТЬ 1 СТЕРЖНЯ НАПРАВЛЕНА ПО ЧАСОВОЙ СТРЕЛКЕ).
Пересекаем перпендикуляры к скоростям на концах стержня 3 – точка пересечения мгновенный центр скоростей стержня 3.
Вариант 2: в Дано задана ω1, 1/c – угловая скорость стержня 1 (на рисунке направлена против хода часовой стрелки).
Определяем направление и значение скорости на конце стержня 1 (скорость V перпендикулярна стержню 1; V= ω1l1)
Анализируем, какому еще стержню принадлежит конец 1 стержня (стержню 3)
Определяем направление скорости второго конца данного стержня (ползун движется вертикально вверх).
Пересекаем перпендикуляры к скоростям на концах стержня 3 – точка пересечения мгновенный центр скоростей стержня 3.

2. Определение скоростей всех точек механизма, отмеченных буквами на схеме, и угловых скоростей всех стержней.

.
2. Определение скоростей всех точек механизма, отмеченных буквами на схеме, и угловых скоростей всех стержней.
Определяем направление скорости точки D (перпендикулярна линии, соединяющей D и МЦС3)
Анализируем, какому еще стержню принадлежит точка D (стержень 2).
Определяем направление скорости второго конца данного стержня (скорость VE перпендикулярна стержню 4, т.к. точка E движется по дуге окружности вокруг точки О2 – УГЛОВАЯ СКОРОСТЬ 4 СТЕРЖНЯ НАПРАВЛЕНА ПО ЧАСОВОЙ СТРЕЛКЕ).
Пересекаем перпендикуляры к скоростям на концах стержня 2 – точка пересечения мгновенный центр скоростей стержня 2.

2. Определение скоростей всех точек механизма, отмеченных буквами на схеме, и угловых скоростей всех стержней.

2. Определение скоростей всех точек механизма, отмеченных буквами на схеме, и угловых скоростей всех стержней.

4. Выводы:
1) Мгновенный центр скоростей – точка скорость, которой равна 0.
2) Мгновенный центр скоростей получается пересечением перпендикуляров к скоростям на концах стержня – точка вокруг, которой вращается стержень.
3) Скорость точки определяется по формуле: V = ωR, где R – расстояние от точки до мгновенного центра скоростей.

Разбор задания №5 «Статика. Равновесие тела под действием плоской системы сил»:
1.Выбор исходных данных.
2.Нанесение внешних сил на схему. Проекции сил.
3.Нанесение реакций опор на схему. Виды опор и опорных реакций.
4.Составление уравнений равновесия. Определение момента силы.
5.Выводы.

1. Выбор исходных данных (продолжение)
Если, например, АБВ =092, то из таблицы исходных данных:
Наносим на схему все внешние силы (F1, F2, P) и моменты (M).

2. Определение реакций опор.
Конструкция связана с поверхностью через опоры связями (реакциями опор). Рассмотрим основные виды опор и опорных реакций:
2.1. Нанесение на схему реакций опор.

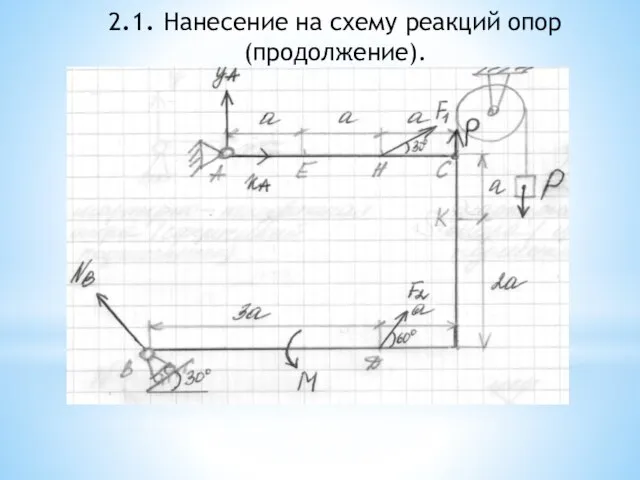
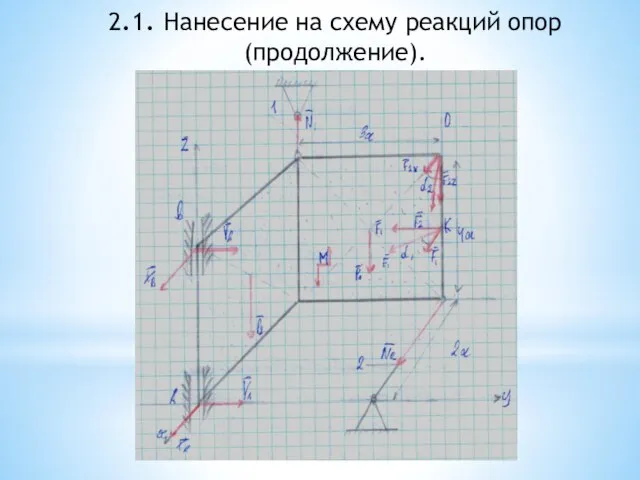
2.1. Нанесение на схему реакций опор (продолжение).

.
2.2. Разложение сил на проекции.
Для удобства расчетов раскладываем силы на проекции. Рассмотрим пример разложения силы на проекции:
Вектор силы, которая находится под углом к оси, можно разложить на проекции.
Тогда проекция вектора силы F1 на ось будет равна произведению:
модуля силы F1 на косинус угла (cosa), если a прилежит к оси (касается оси);
модуля силы F1 на синус угла (sina), если a противолежит (лежит напротив) оси.

2.2. Разложение сил на проекции (продолжение)
Разложим силы F1, F2 и реакцию NB на проекции.

3. Составление уравнений равновесия.
3.1. Понятие момента силы.
Момент силы F относительно точки A равен произведению силы F на плечо h (момент равен силе, умноженной на плечо) с учетом знака («+» против хода часовой стрелки).
Плечо h кратчайшее расстояние (перпендикуляр) от линии действия силы до точки (полюса).

3.2. Общий вид уравнений равновесия.
При решении задач равновесия тела под действием плоской системы сил общий вид уравнений равновесия имеет вид (система трех уравнений):
3. Составление уравнений равновесия.
ИЛИ

3. Составление уравнений равновесия (продолжение)
Составим уравнение 1 и 2 для рассматриваемой задачи. Проецируем все силы и реакции на ось x и ось y, если направление силы совпадает с направлением оси (справа налево и снизу вверх соответственно), то перед силой ставится «+», иначе «-».

3. Составление уравнений равновесия (продолжение)
Составим уравнение 3 для рассматриваемой задачи. Записываем сумму моментов от всех сил и реакций относительно точки A (берется опора, в которой больше неизвестных реакций). Знак момента принимается «+», если сила вращает вокруг точки А против хода часовой стрелки, иначе «-».

3. Составление уравнений равновесия (продолжение)
Уравнения равновесия для рассматриваемой задачи:
После составления уравнений равновесия выражаем неизвестные Xa, Ya, NB, подставляем числовые значения и получаем их значения. Полученные значения записываем в ответ.

3. Составление уравнений равновесия (продолжение)
Из уравнения 3:
Из уравнения 1:

3. Составление уравнений равновесия (продолжение)
Из уравнения 2:
Тогда реакция в точке А (RA):
В ответ запишется:

4. Выводы.
1.Статикой называют раздел теоретической механики, изучающий равновесие тел.
2. Момент силы F относительно точки A равен произведению силы F на плечо h (момент равен силе, умноженной на плечо).
3. Знак момента принимается «+», если сила вращает вокруг точки А против хода часовой стрелки, иначе «-».
4. Плечо h кратчайшее расстояние (перпендикуляр) от линии действия силы до точки (полюса).
5. Для решения задачи равновесия тел под действием плоской системы сил составляется система из 3 уравнений статики.

Разбор задания №5 «Статика. Равновесие тела под действием плоской системы сил»:
1.Выбор исходных данных. Нанесение внешних сил на схему. Проекции сил.
2. Нанесение реакций опор на схему.
3.Разделение конструкции на 2 тела. Учет реакций в месте соприкосновения 2 тел. Составление уравнений равновесия.
4.Выводы.

1. Выбор исходных данных (продолжение)
Если, например, АБВ =092, то из таблицы исходных данных:
Наносим на схему все внешние силы (F1, F2), распределенную нагрузку (q) и момент (M).

2.1. Нанесение на схему реакций опор (продолжение).

3.1. Общий вид уравнений равновесия для задач равновесия двух тел.
При решении задач равновесия 2 тел под действием плоской системы сил общий вид уравнений равновесия имеет вид системы 6 уравнений (3 уравнения равновесия для первого тела и 3 уравнения равновесия для второго тела).
Конструкцию разделяют в месте соединения (врезанный шарнир или точка опирания) на 2 тела при этом учитываются реакции в месте соединения:
на каждом теле в точке соединения рисуем реакцию Rc (реакция Rc на первом и втором теле имеет одинаковое значение, но противоположное направление)
Замечание: в случае соединения через врезанный шарнир на каждом теле в точке соединения разбиваем реакцию Rc на проекции Xc и Yc.
3. Разделение конструкции на 2 тела. Составление уравнений равновесия.

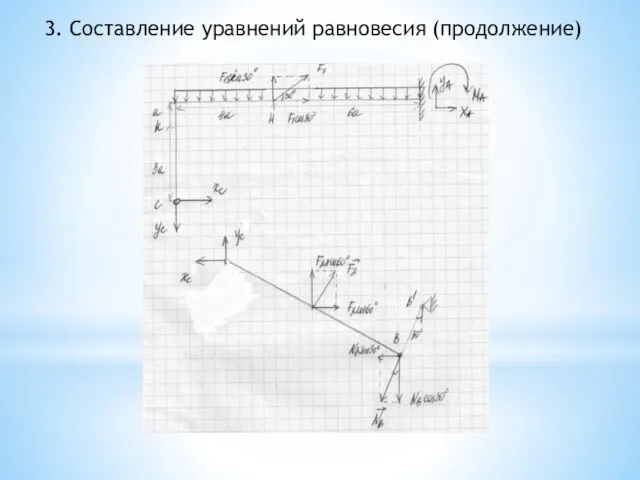
3. Составление уравнений равновесия (продолжение)

3. Составление уравнений равновесия (продолжение). Распределенная нагрузка q
Прежде чем приступать к составлению уравнений равновесия рассмотрим понятие «распределенной нагрузки q», которая задана в исходных данных значением 20 [кН/м] и участком приложения АЕ.
Заметим из единиц измерения [кН/м], что «распределенная нагрузка q» является силой, распределенной по длине (участок АЕ).
Чтобы включать данную нагрузку в уравнения равновесия было проще можно считать распределенную нагрузку q эквивалентной сосредоточенной силе Q, равной произведению q на длину распределения (участок АЕ) и приложенной в центр длины распределения (середина участка АЕ).

3. Составление уравнений равновесия (продолжение)
Составление уравнений равновесия в общем виде начинаем с того тела, на котором меньше неизвестных реакций (тело 2: Xc, Yc, NB; тело 1: Xa, Ya, Ma, Xc, Yc).

3. Составление уравнений равновесия (продолжение)
Составим уравнение 1 и 2 для рассматриваемой задачи (тело 2). Проецируем все силы и реакции на ось x и ось y, если направление силы совпадает с направлением оси (справа налево и снизу вверх соответственно), то перед силой ставится «+», иначе «-».

3. Составление уравнений равновесия (продолжение)
Составим уравнение 3 для тела 2. Записываем сумму моментов от всех сил и реакций, приложенных к телу 2, относительно точки С (берется опора, в которой больше неизвестных реакций). Знак момента принимается «+», если сила вращает вокруг точки С против хода часовой стрелки, иначе «-».

3. Составление уравнений равновесия (продолжение)
Составим уравнения 4,5 и 6 для тела 1. Записываем суммы моментов от всех сил и реакций, приложенных к телу 1, относительно точек A и C. Знак момента принимается «+», если сила вращает вокруг точки А и С соответственно против хода часовой стрелки, иначе «-». Затем записываем сумму сил и реакций на ось X.

3. Составление уравнений равновесия (продолжение)
Уравнения равновесия для рассматриваемой задачи:
После составления уравнений равновесия выражаем неизвестные Xс, Yс, NB из уравнений для тела 2, подставляем числовые значения и получаем их значения. Теперь, когда известны значения Хс и Yc из уравнений для тела 1 выражаем неизвестные Xa, Ya и Ma. Полученные значения записываем в ответ.

3. Составление уравнений равновесия (продолжение)
Из уравнения 3:
Из уравнения 1:

3. Составление уравнений равновесия (продолжение)
Из уравнения 2:
Тогда реакция в точке С (Rс):
Из уравнения 4:

3. Составление уравнений равновесия (продолжение)
Из уравнения 6:
Из уравнения 5:

3. Составление уравнений равновесия (продолжение)
Тогда реакция в точке A (Ra): В ответ запишется:

4. Выводы.
1.Статикой называют раздел теоретической механики, изучающий равновесие тел.
2. Момент силы F относительно точки A равен произведению силы F на плечо h (момент равен силе, умноженной на плечо).
3. Знак момента принимается «+», если сила вращает вокруг точки А против хода часовой стрелки, иначе «-».
4. Плечо h кратчайшее расстояние (перпендикуляр) от линии действия силы до точки (полюса).
5. Распределенную нагрузку q, приложенную на участке длиной l, можно заменить сосредоточенной силой Q, равной произведению q на длину участка распределения l и приложенной в центр участка распределения.
6. Для решения задачи равновесия 2 тел под действием плоской системы сил составляется система из 6 уравнений статики.

Разбор задания №7 «Статика. Равновесие тела под действием пространственной системы сил»:
1.Выбор исходных данных. Нанесение внешних сил на схему. Проекции сил.
2. Нанесение реакций опор на схему.
3. Составление уравнений равновесия. Момент силы относительно оси.
4.Выводы.

1. Выбор исходных данных (продолжение)
Если, например, АБВ =882, то из таблицы исходных данных:
Наносим на схему внешние силы (F1, F2),) и момент (M). Обратим внимание на положение осей Oxyz.

2.1. Нанесение на схему реакций опор (продолжение).

3.1. Общий вид уравнений равновесия для задач равновесия тела под действием пространственной системы сил.
При решении задач равновесия тела под действием пространственной системы сил общий вид уравнений равновесия имеет вид системы 6 уравнений (3 уравнения равновесия сил и 3 уравнения равновесия моментов).
3. Составление уравнений равновесия.
При решении данной системы 6 уравнений будут определены 6 неизвестных реакций опор.

3. Составление уравнений равновесия (продолжение)

3. Составление уравнений равновесия (продолжение). Момент относительно оси
Прежде чем приступать к составлению оставшихся уравнений равновесия рассмотрим понятие «момент M относительно оси», т.к. 3 оставшихся уравнения равновесия – это уравнения равновесия моментов вокруг осей x, y и z соответственно.
Момент силы относительно оси – алгебраическая величина, равная произведению проекции вектора силы на плоскость, перпендикулярную оси, на плечо этой проекции относительно точки пересечения оси с плоскостью, взятая со знаком + (плюс), если вращение плоскости под действием силы представляется при взгляде навстречу оси происходящим против часовой стрелки, и со знаком – (минус) в противном случае.

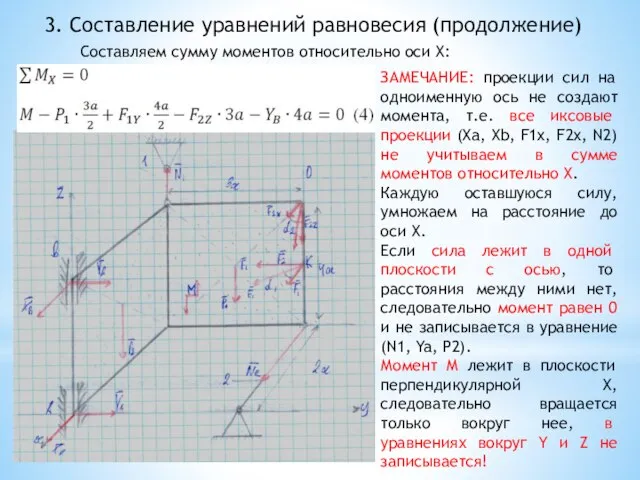
3. Составление уравнений равновесия (продолжение)
Составляем сумму моментов относительно оси X:
ЗАМЕЧАНИЕ: проекции сил на одноименную ось не создают момента, т.е. все иксовые проекции (Xa, Xb, F1x, F2x, N2) не учитываем в сумме моментов относительно X.
Каждую оставшуюся силу, умножаем на расстояние до оси Х.
Если сила лежит в одной плоскости с осью, то расстояния между ними нет, следовательно момент равен 0 и не записывается в уравнение (N1, Ya, P2).
Момент М лежит в плоскости перпендикулярной Х, следовательно вращается только вокруг нее, в уравнениях вокруг Y и Z не записывается!

3. Составление уравнений равновесия (продолжение)
Составляем сумму моментов относительно оси Y:
ЗАМЕЧАНИЕ: проекции сил на одноименную ось не создают момента, т.е. все игриковые проекции (Ya, Yb, F1y) не учитываем в сумме моментов относительно Y.
Каждую оставшуюся силу, умножаем на расстояние до оси Y.
Если сила лежит в одной плоскости с осью, то расстояния между ними нет, следовательно момент равен 0 и не записывается в уравнение (N2, Xa).
Момент М не лежит в плоскости перпендикулярной Y, следовательно не вращается вокруг нее, в уравнение вокруг Y не записывается!

3. Составление уравнений равновесия (продолжение)
Составляем сумму моментов относительно оси Z:
ЗАМЕЧАНИЕ: проекции сил на одноименную ось не создают момента, т.е. все зэтовые проекции (Р1, P2, F2z, N1) не учитываем в сумме моментов относительно Z.
Каждую оставшуюся силу, умножаем на расстояние до оси Z.
Если сила лежит в одной плоскости с осью, то расстояния между ними нет, следовательно момент равен 0 и не записывается в уравнение (Xa, Xb, Ya, Yb).
Момент М не лежит в плоскости перпендикулярной Z, следовательно не вращается вокруг нее, в уравнение вокруг Z не записывается!

3. Составление уравнений равновесия (продолжение)
Результирующая система уравнений равновесия имеет вид:.
После составления уравнений равновесия выражаем неизвестные Xa, Xb, Ya, Yb, N1 и N2 из уравнений рановесия, подставляем числовые значения и получаем их значения.. Полученные значения записываем в ответ.

3. Составление уравнений равновесия (продолжение)
Из уравнения 3:
Из уравнения 6: Из уравнения 5:

3. Составление уравнений равновесия (продолжение)
Из уравнения 4:
Из уравнения 2: Из уравнения 1:
В ответ запишется:

4. Выводы.
1.Статикой называют раздел теоретической механики, изучающий равновесие тел.
2. Момент силы F относительно точки A равен произведению силы F на плечо h (момент равен силе, умноженной на плечо).
3. Знак момента принимается «+», если сила вращает вокруг точки А против хода часовой стрелки, иначе «-».
4. Момент силы относительно оси – алгебраическая величина, равная произведению проекции вектора силы на плоскость, перпендикулярную оси, на плечо этой проекции относительно точки пересечения оси с плоскостью, взятая со знаком + (плюс), если вращение плоскости под действием силы представляется при взгляде навстречу оси происходящим против часовой стрелки, и со знаком – (минус) в противном случае.
5. При решении задачи на равновесие тела под действием пространственной системы сил составляются 6 уравнений равновесия (3 уравнения сил и 3 уравнения моментов).

Подготовка к зачету!
I. Найдите реакции опор в следующей задаче:
1. Обозначить реакции на схеме

Подготовка к зачету!
I. Найдите реакции опор в следующей задаче:
1. Обозначить реакции на схеме

Подготовка к зачету!
I. Найдите реакции опор в следующей задаче:
1. Обозначить реакции на схеме

Подготовка к зачету!
I. Найдите реакции опор в следующей задаче:
1. Обозначить реакции на схеме

Подготовка к зачету!
I. Найдите реакции опор в следующей задаче:
1. Обозначить реакции на схеме

Разбор задания №8 «Динамика материальной точки»:
1.Выбор исходных данных. Нанесение внешних сил на схему. Проекции сил.
2. Составление дифференциального уравнения движения груза.
3. Нахождения закона движения груза по начальным условиям.
4.Выводы.

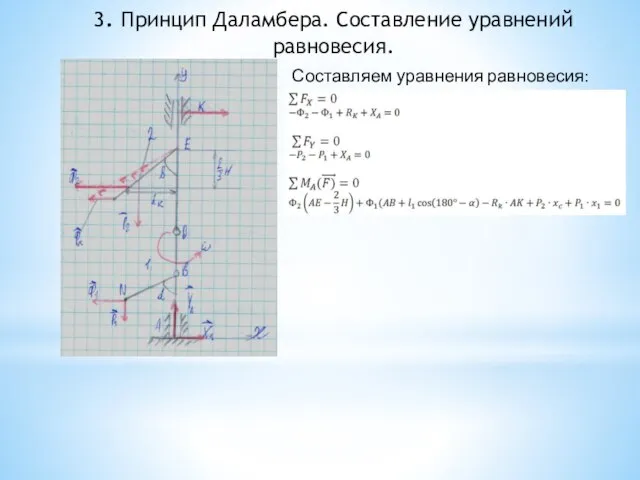
Разбор задания №9 «Динамика. Принцип Даламбера»:
1.Выбор исходных данных. Нанесение внешних сил на схему.
2. Принцип Даламбера. Нанесение на схему сил инерции. Нанесение на схему реакций опор.
3. Составление уравнений равновесия. Нахождение реакций опор.
4.Выводы.

1. Выбор исходных данных (продолжение)
Если, например, АБВ =884, то из таблицы исходных данных:
Наносим на схему внешнюю силу (F).

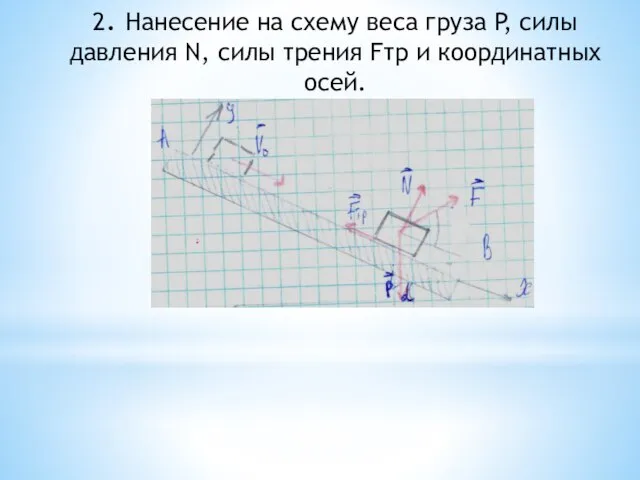
2. Нанесение на схему веса груза P, силы давления N, силы трения Fтр и координатных осей.

Общий вид дифференциального уравнения движения груза по наклонной плоскости:
3. Составление дифференциального уравнения движения груза.
Проецируем уравнение движения на оси координат X и Y:
Т.к. тело движется по оси X, то и из проекции на ось Y имеем :

3. Составление дифференциального уравнения движения груза (продолжение)
Учитывая, что из проекции на ось X имеем :
Интегрируем полученное выражение:

3. Составление дифференциального уравнения движения груза (продолжение)
Т.к. в начальный момент времени t=0 V0=40 м/с:
Получаем закон изменения скорости тела под действием силы F:

3. Составление дифференциального уравнения движения груза (продолжение)
Снова интегрируем:
Система координат выбрана так, что X0=0:
В ответ записываем закон движения тела:

1. Выбор исходных данных (продолжение)
Если, например, АБВ =884, то из таблицы исходных данных:
Наносим на схему стержень 1 с массой, сосредоточенной на конце, и стержень 2, с равномерно распределенной массой и угловую скорость вращения w.

2. Принцип Даламбера. Нанесение на схему веса стержней, сил инерции и реакций опор.
Согласно принципу Даламбера: все действующие на систему силы вместе с силами инерции образуют уравновешенную плоскую систему сил.
Т.к. вал вращается равномерно точки стержня имеют только нормальное ускорение an, направленное к оси вращения
Силы инерции вычисляются, как
Поскольку все силы инерции Фк пропорциональны hk, то эпыра образует треугольник, который можно заменить равнодействующей Ф2 , приложенной в центр тяжести треугольника, т.е. на расстоянии 2/3Н от вершины.

2. Принцип Даламбера. Нанесение на схему веса стержней, сил инерции и реакций опор.
Сила инерции стержня с распределенной массой определяется, как
где ac – ускорение центра стержня 2.
Сила инерции стержня с сосредоточенной массой определяется, как

3. Принцип Даламбера. Составление уравнений равновесия.
Составляем уравнения равновесия:

4. Выводы.
1.Динамикой называют раздел теоретической механики, изучающий равновесие движущихся систем.
2. При решении задачи на определение закона движения тела, следует составить дифференциальное уравнение равновесия и проинтегрировать его дважды с учетом начальных условий.
3. При решении задачи на определение реакций опор в движущейся системе, следует составить уравнения равновесия включив в них силы инерции, согласно принципу Даламбера.
4. Принцип Даламбера: все действующие на систему силы вместе с силами инерции образуют уравновешенную плоскую систему сил.

Подготовка к зачету!
I. Найдите реакции опор в следующих задачах самостоятельно:

Подготовка к зачету!
I. Найдите реакции опор в следующих задачах самостоятельно: