Содержание
- 2. Результаты, основанные на статистике Основное уравнение состояния идеального газа и УМК : Р = nkT =>
- 3. Теория игр «Орлянка» и «игра в кости» Вероятности
- 4. Игры в «орлянку» и в «кости» ПРИМЕР 1: Бросаем монетку. Результат испытаний: тип 1 – если
- 5. Сложение и умножение вероятностей. Pi или k = Немного математики - вероятность P i или k
- 6. N – общее число испытаний, Ni – число испытаний с результатом типа i Рi – вероятность
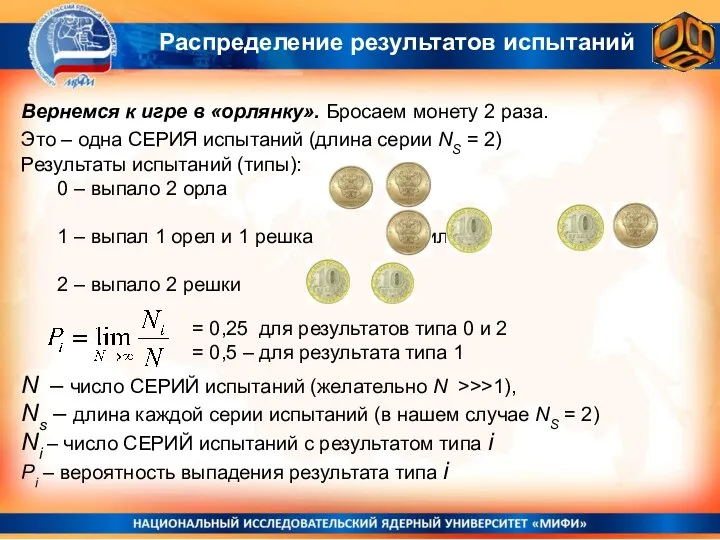
- 7. Распределение результатов испытаний Вернемся к игре в «орлянку». Бросаем монету 2 раза. Это – одна СЕРИЯ
- 8. Бросаем монетку N раз. Это – одна серия испытаний длиной N Нумеруем все результаты (типы результатов)
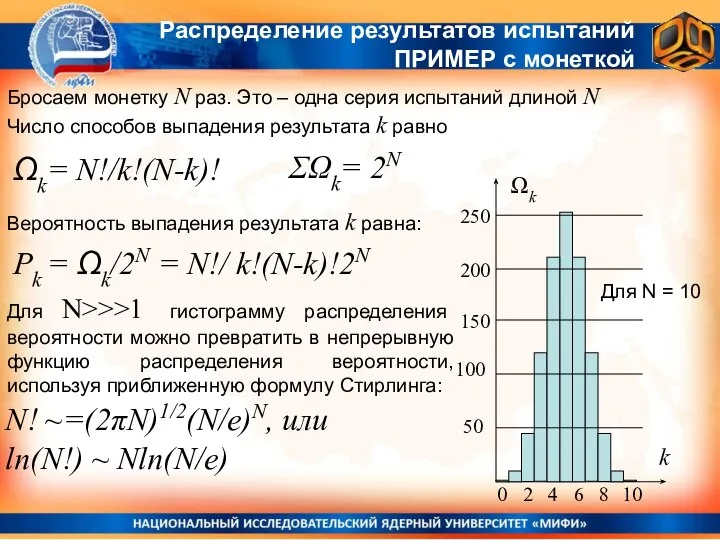
- 9. Бросаем монетку N раз. Это – одна серия испытаний длиной N Число способов выпадения результата k
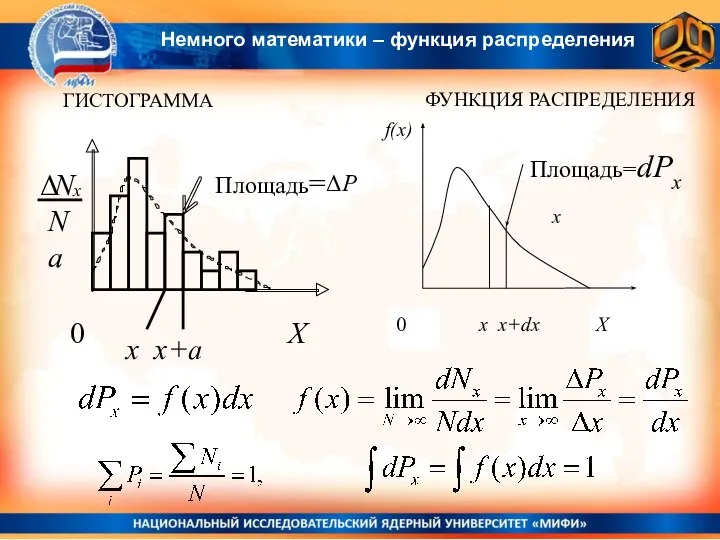
- 10. ГИСТОГРАММА ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ x x+a ΔP x Немного математики – функция распределения
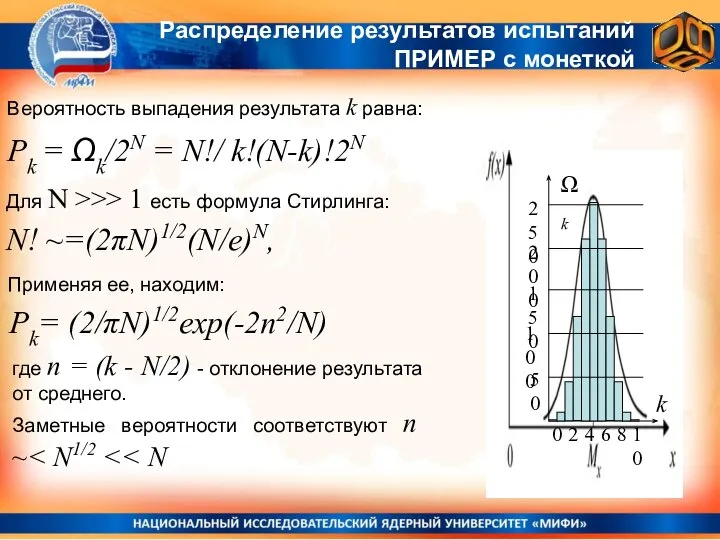
- 11. Распределение результатов испытаний ПРИМЕР с монеткой Вероятность выпадения результата k равна: Pk = Ωk/2N = N!/
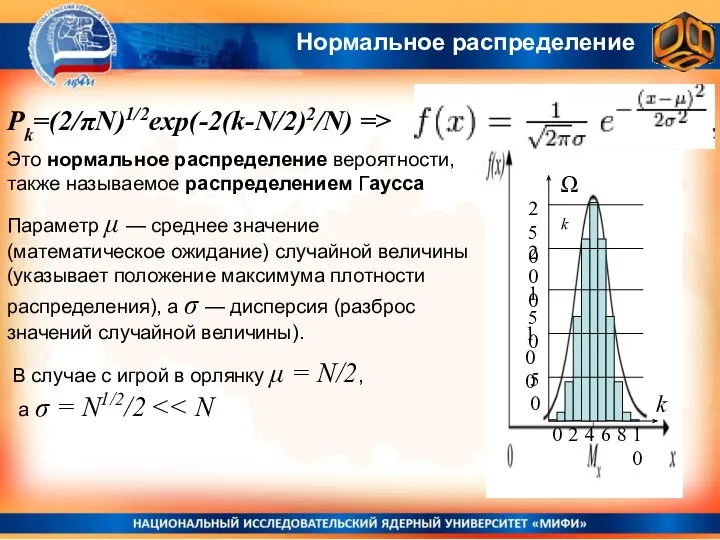
- 12. Нормальное распределение Это нормальное распределение вероятности, также называемое распределением Гаусса Параметр μ — среднее значение (математическое
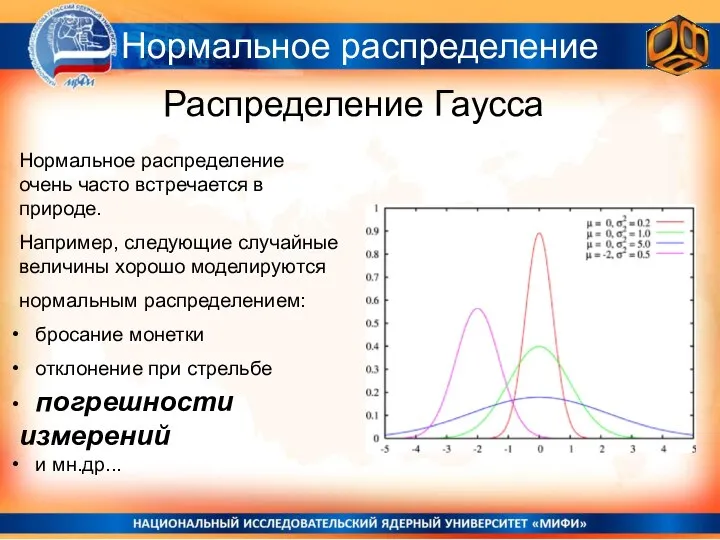
- 13. Распределение Гаусса Нормальное распределение Нормальное распределение очень часто встречается в природе. Например, следующие случайные величины хорошо
- 14. Распределение Гаусса Энтропия в информатике и в статистической физике Курс общей физики НИЯУ МИФИ
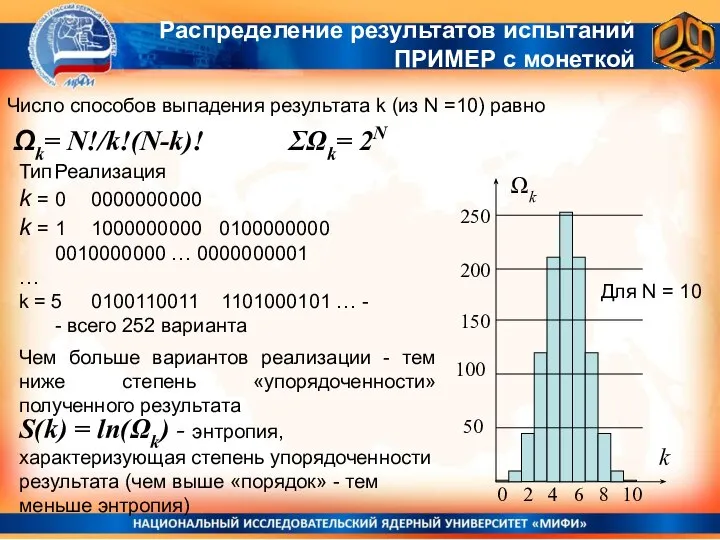
- 15. Число способов выпадения результата k (из N =10) равно Ωk= N!/k!(N-k)! Распределение результатов испытаний ПРИМЕР с
- 16. Энтропия вероятности S(k) = ln(Ωk) - энтропия, характеризующая степень упорядоченности результата Для N = 10 S(k)
- 17. Информационная энтропия Тип Реализация k = 0 0000000000 k = 1 1000000000 0100000000 ... k =
- 18. Информационная энтропия Любое информационное сообщение можно представить в виде двоичного кода: 0110010101110010010101111110001010111…. S(N,k) = ln(ΩN,k), где
- 19. Информационная энтропия Понятие энтропии, как меры случайности и беспорядка в информационных системах, впервые введено Клодом Шенноном
- 20. Энтропия в статистической физике и термодинамическая энтропия Курс общей физики НИЯУ МИФИ
- 21. Задача о распределении по ячейкам Пусть у нас есть К ячеек (состояний) по которым распределены N
- 22. В равновесном состоянии система описывается макропараметрами: энтропию равновесного состояния должно быть можно выразить через макропараметры. ~
- 23. Энтропия макро-состояния системы в статистической физике = логарифм от числа возможных микро-реализаций этого состояния Она совпадает
- 25. Скачать презентацию















 Электроника и микропроцессорная техника
Электроника и микропроцессорная техника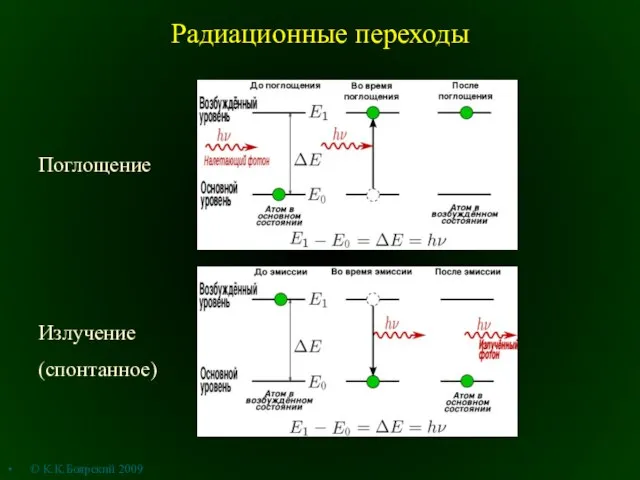 Радиационные переходы
Радиационные переходы Аттестационная работа: Элективный курс Строение и свойство вещества
Аттестационная работа: Элективный курс Строение и свойство вещества Что значит минута
Что значит минута Программа элективного курса: Чудеса физики
Программа элективного курса: Чудеса физики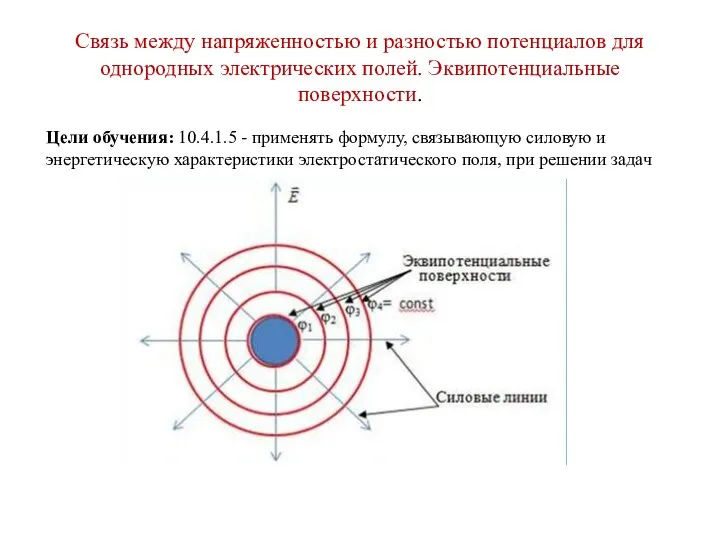 Эквипотенциальные поверхности
Эквипотенциальные поверхности Классификация навигационных систем. Параметры движения в пространстве
Классификация навигационных систем. Параметры движения в пространстве Агрегатные состояния вещества
Агрегатные состояния вещества Математическое моделирование физических процессов. Иллюстрационные материалы
Математическое моделирование физических процессов. Иллюстрационные материалы Международная ассоциация дилеров ПАО Автоваз. Наиболее распространенные дефекты
Международная ассоциация дилеров ПАО Автоваз. Наиболее распространенные дефекты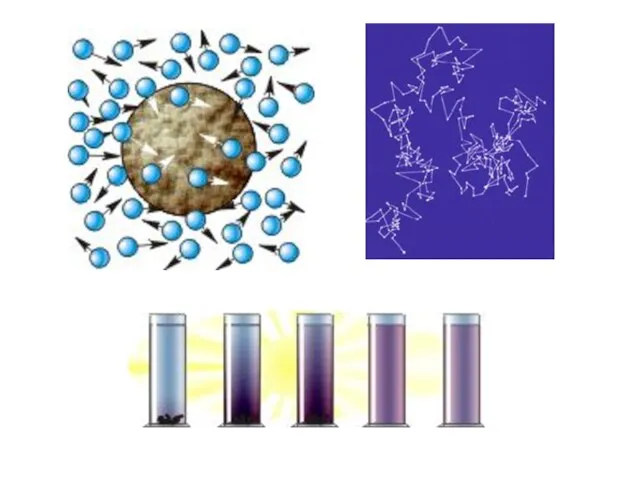 Тепловое движение
Тепловое движение Звездный час. Мероприятие по физике
Звездный час. Мероприятие по физике Презентация на тему Квантовая механика
Презентация на тему Квантовая механика  сила Архимеда сила выталкивающая тело из жидкости
сила Архимеда сила выталкивающая тело из жидкости 8 кл 3-4 Вн энергия. виды теплопередачи
8 кл 3-4 Вн энергия. виды теплопередачи Кинематика
Кинематика Закон сохранения энергии, работа и мощность в механике
Закон сохранения энергии, работа и мощность в механике Презентация на тему Опасная инерция
Презентация на тему Опасная инерция 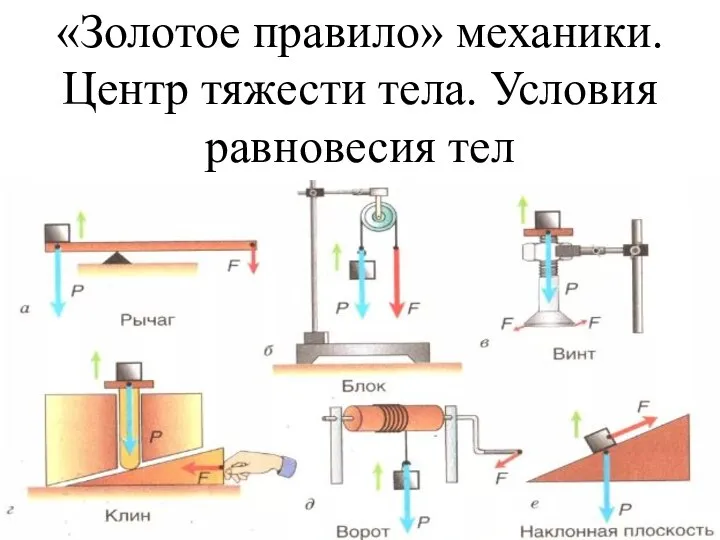 Золотое правило механики. Центр тяжести тела. Условия равновесия тел
Золотое правило механики. Центр тяжести тела. Условия равновесия тел Ультрофеолетовые волны
Ультрофеолетовые волны Подготовка к КДР (краевые диагностические работы)
Подготовка к КДР (краевые диагностические работы) Сцепление. Тесты к теоретическим занятиям
Сцепление. Тесты к теоретическим занятиям Меры защиты человека при косвенном прикосновении. Устройство защитного отключения (УЗО) на дифференциальном токе
Меры защиты человека при косвенном прикосновении. Устройство защитного отключения (УЗО) на дифференциальном токе Электромагниты и их применение
Электромагниты и их применение Резание тонколистового металла и проволоки
Резание тонколистового металла и проволоки Линейные размеры в СТО Автор Skyfury Sparkle
Линейные размеры в СТО Автор Skyfury Sparkle Определение толщины зуба на любом радиусе
Определение толщины зуба на любом радиусе Оптика. Закон отражения света
Оптика. Закон отражения света